【深度学习】激活函数

目录

0 激活函数

1 sigmoid函数

2 阶跃函数

3 ReLU函数

4 Leaky ReLU函数

5 tanh函数

0 激活函数

激活函数（Activation functions）是神经网络的必要组成部分。以阈值为界，一旦输入超过阈值，就切换输出。

激活函数作用：激活函数是用来加入非线性因素的，增加模型的表达能力。因为线性模型的表达能力不够。

如果没有激活函数，多次线性运算的堆叠仍然是一个线性的运算，即不管用再多的层实质上只起到了一层神经网络的作用。一个好的激活函数，应当满足：

（1）不会饱和

sigmoid和tanh激活函数在两侧尾端会有饱和现象，这会使导数在这些区域接近零，从而阻碍网络的训练；

（2）零均值

ReLU激活函数的输出均值不为零，这会影响网络的训练；

（3）容易计算

1 sigmoid函数

最常使用的激活函数就是sigmoid函数(sigmoid function).在tensorflow中表示为

tf.nn.sigmoid()

python实现

# coding: utf-8
import numpy as np
import matplotlib.pylab as plt


def sigmoid(x):
    return 1 / (1 + np.exp(-x))    

X = np.arange(-5.0, 5.0, 0.1)
Y = sigmoid(X)
plt.plot(X, Y)
plt.ylim(-0.1, 1.1)
plt.show()

 

sigmoid函数图像

2 阶跃函数

阶跃函数，当输出超过0时，输出1，小于0时，输出0

python实现

# coding: utf-8
import numpy as np
import matplotlib.pylab as plt


def step_function(x):
    return np.array(x > 0, dtype=np.int)

X = np.arange(-5.0, 5.0, 0.1)
Y = step_function(X)
plt.plot(X, Y)
plt.ylim(-0.1, 1.1)  # 指定图中绘制的y轴的范围
plt.show()

 

阶跃函数图像

3 ReLU函数

ReLU函数在输入大于等于0时，直接输出该值，在输入小于等于0时，输出0；在tensorflow中表示为:

tf.nn.relu()

python实现

# coding: utf-8
import numpy as np
import matplotlib.pylab as plt


def relu(x):
    return np.maximum(0, x)

x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)
plt.plot(x, y)
plt.ylim(-1.0, 5.5)
plt.show()

ReLU函数图像

4 Leaky ReLU函数

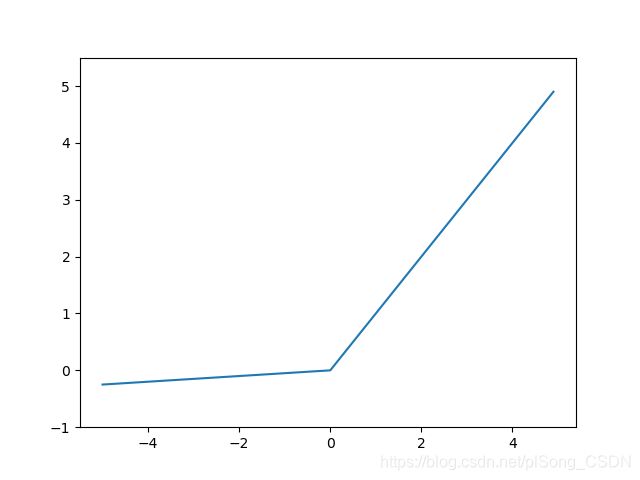
ReLU是将所有的负值都设为0，相反，Leaky ReLU是给所有负值赋予一个非零斜率。改模型在2013年首次在声学模型中使用。

python实现

# coding: utf-8
import numpy as np
import matplotlib.pylab as plt


def leaky_relu(x):
    return np.maximum(x/20, x) # 这里a取20

x = np.arange(-5.0, 5.0, 0.1)
y = leaky_relu(x)
plt.plot(x, y)
plt.ylim(-1.0, 5.5)
plt.show()

 

Leaky ReLU函数图像

5 tanh函数

在tensorflow中表示为：

tf.nn.tanh()

表达式为：

python实现

import numpy as np
import matplotlib.pylab as plt

def tanh(x):
    return (1-np.exp(-2*x)) / (1+np.exp(-2*x))

X = np.arange(-5.0,5.0,0.1)
Y = tanh(X)
plt.plot(X,Y)
plt.show()

 

 

---

★finished by songpl,2019.1.9