【TSP问题】TSP问题有关解法
TSP问题有关解法
- 近似算法
-
- 基本思想
- 代码
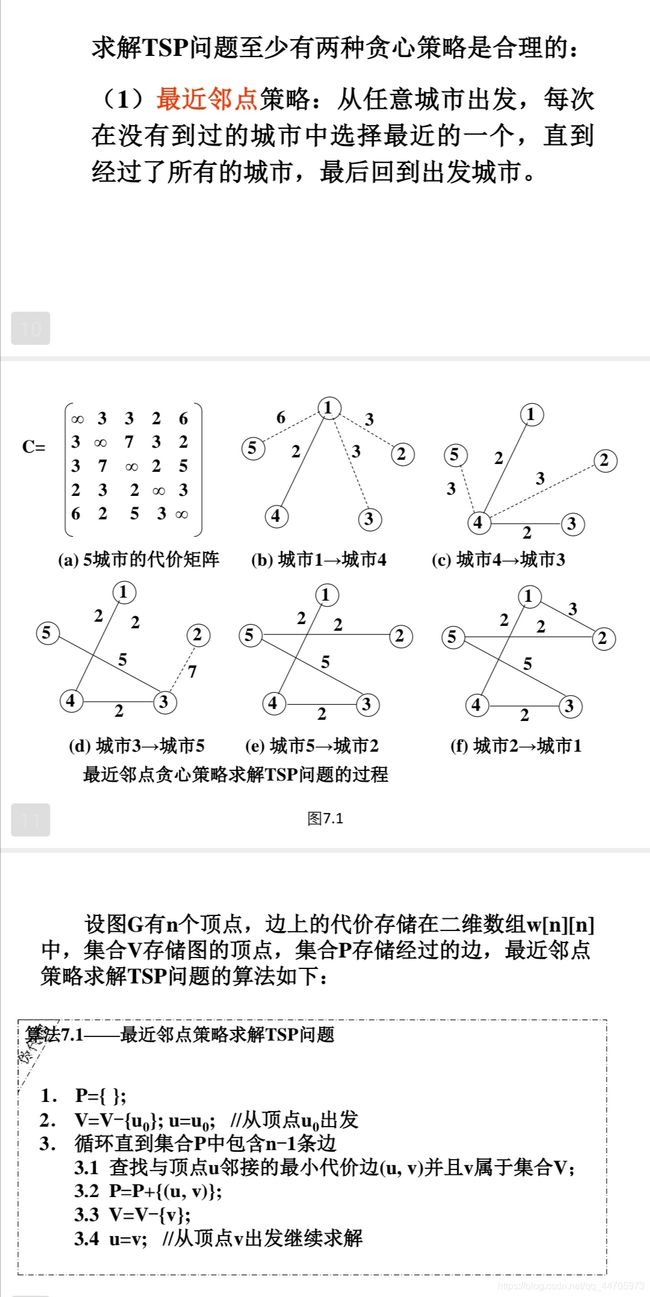
- 贪心算法
-
- 基本思想
- 代码
- 分支限界法(与贪心算法结合)
-
- 基本思想
- 代码
- 动态规划算法(与回溯法相结合)
-
- 基本思想
- 代码
- 遗传算法
- 蚁群算法
TSP问题可以有很多种解决方法,比如动态规划、蛮力算法,贪心算法、近似算法、蚁群算法、遗传算法、分支限界法等等。之前课程作业也做过很多有关TSP问题的习题。所以想把这些都总结一下,方便以后作为复习。
近似算法
基本思想
代码
#include
if (p == -1) break;
vis[p] = 1;//标记
int pa = parent[p];
if (pa != -1)
{
//cout << p << " " << pa << endl;
res.add_edge(p, pa, 1);//往最小生成树里面加一条边
}
for (int j = 0; j<n; j++)
{
if (!vis[j] && adj[p][j]<lowcost[j])//更新最小代价和路径
{
lowcost[j] = adj[p][j];
parent[j] = p;
}
}
}
return res;
}
vector<int> dfs(int u_id)//深度优先遍历
{
vector<int> vis(n, 0);
vector<int> res;
stack<int> s;//栈
s.push(u_id);
vis[u_id] = 1;
while (!s.empty())
{
int x = s.top();//取栈顶的元素
s.pop();
res.push_back(x);
for (int i = 0; i < n; i++)//遍历后继结点
{
if (adj[x][i]!=-1 && vis[i] == 0)
{
vis[i] = 1;//标记
s.push(i);//入栈
}
}
}
return res;
}
};
int main()
{
int n;
cin >> n;
Graph graph(n);
graph.input();
Graph tree = graph.get_tree(0);//以0为起点
vector<int> v = tree.dfs(0);//以0为起点
for (int i = 0; i < v.size(); i++)
{
cout << v[i] << " ";
}
cout << endl;
return 0;
}
/*
5
10000000 10 6 8 7
10 10000000 5 22 1
6 5 10000000 11 7
8 22 11 10000000 3
7 1 7 3 10000000
*/
贪心算法
基本思想
代码
//贪心法求解TSP问题
#include分支限界法(与贪心算法结合)
基本思想
代码
#include 动态规划算法(与回溯法相结合)
基本思想
代码
#include遗传算法
思路在前面,就不再写了。
#include 蚁群算法
#include