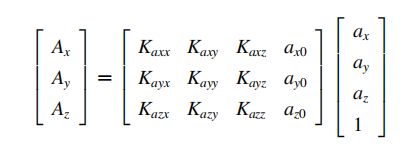MEMS惯性导航单元的标定与测试
本文的标定与测试的流程主要参考国家计量技术规范:
(1)微机电(MEMS)陀螺仪校准规范 JJF 1535-2015
(2)微机电线加速度计校准规范 JJF 1427-2013
一、MEMS惯性导航单元
MEMS惯性导航单元主要由三轴加速度计和三轴陀螺仪组成,其主要的性能基本由陀螺仪决定,因为一般而言MEMS陀螺仪性能相较于加速度计较差,其次由于陀螺仪感应惯性-载体系角速度即 w i b w_{ib} wib,由此计算得到航向角、横滚角、俯仰角等信息,角度误差会导致速度误差的加剧,因此在MEMS惯性导航单元中一般主要关注陀螺仪的性能,其中陀螺仪的性能又更关注于零偏稳定性的性能,因为零偏稳定性通常能表现该惯导的“波动”的程度。
本文主要针对以下参数进行了标定与测试:
陀螺仪:标度因数、标度因数非线性、安装误差、标度因数不对称性、零偏、零偏稳定性(静态)、Allan方差、阈值、分辨率。
加速度计:偏值、标度因数、安装误差、非线性度(离心机实验)、0g/1g稳定性、阈值、分辨率。
其中离心机实验由于条件限制,采用了重力激励替代离心机,在0-1g的范围内测量了非线性度。
二、加速度计标定
2.1 标度因数、安装误差以及零偏(偏值)
标度因数、安装误差以及零偏(偏值)采用最小二乘法拟合。
F = K ∗ Ω + F 0 F = K*\Omega+F_0 F=K∗Ω+F0
其中, F 0 F_0 F0为偏值,标度因数为 K K K。
上述公式是针对一个加速度计的,安装误差是存在于三个加速度计之间,成因是由于安装工艺的限制,导致三个加速度计轴向之间不是绝对的90°,不完全正交。
[ A x A y A z ] = [ a x 0 a y 0 a z 0 ] + [ K a x x K a x y K a x z K a y x K a y y K a y z K a z x K a z y K a z z ] [ a x a y a z ] + [ Δ r x Δ r y Δ r z ] \left[\begin{array}{l}A_{x} \\ A_{y} \\ A_{z}\end{array}\right]=\left[\begin{array}{l}a_{x 0} \\ a_{y 0} \\ a_{z 0}\end{array}\right]+\left[\begin{array}{ccc}K_{a x x} & K_{a x y} & K_{a x z} \\ K_{a y x} & K_{a y y} & K_{a y z} \\ K_{a z x} & K_{a z y} & K_{a z z}\end{array}\right]\left[\begin{array}{l}a_{x} \\ a_{y} \\ a_{z}\end{array}\right]+\left[\begin{array}{c}\Delta_{r x} \\ \Delta_{r y} \\ \Delta_{r z}\end{array}\right] ⎣⎡AxAyAz⎦⎤=⎣⎡ax0ay0az0⎦⎤+⎣⎡KaxxKayxKazxKaxyKayyKazyKaxzKayzKazz⎦⎤⎣⎡axayaz⎦⎤+⎣⎡ΔrxΔryΔrz⎦⎤
其中, a 0 a_0 a0为零偏, K a ∗ ∗ K_{a**} Ka∗∗为标度因数, K a ⋅ ∗ K_{a·*} Ka⋅∗为安装误差, Δ r \Delta_r Δr为随机漂移。
在 K a ⋅ ∗ K_{a·*} Ka⋅∗组成的矩阵中对角线上为每个轴加速度计的标度因数,非对角线上即为三轴之间的安装误差,其中的值取决于两两轴之间的安装误差角度决定。
具体的理论参考相关论文或书籍,例如:严恭敏《捷联惯导算法与组合导航原理》。
一般而言上述的数值计算是采用最小二乘法,因为采集到的数据由于存在波动性,以及器件自身的测量也存在非线性,因此需要采用最小二乘从中拟合最优直线,观察公式中,每个加速度计存在四个未知变量,因此根据线性代数的知识可知至少需要四个相互正交的位置的三轴加速度计的测量值才可以计算出上述公式中所有的变量,在实际操作中,一般采用六位置法、十二位置法以及二十四位置法,位置越多越可以抵消一些现实因素带来的影响。比如十二位置法可以消除平面不水平的影响,二十四位置法可以抵消平面不对称、不水平等影响。
clear;
close all;
clc;
format compact;
% 2021.6 In NJUST by MaYiming
%% 初始化
% 实验室经度118.8533457,纬度32.0292177,高度19.938
% txt数据格式
% 帧计数 wx wy wz ax ay az 从19-24列
% x轴为例:Ax=Aax*Xa;
% Ax,量测矩阵;Aax,观测矩阵;Xa,误差阵
% 最小二乘法拟合
file = {'天东北.txt';'天西南.txt';'地东南.txt';'地西北.txt';...
'东天南.txt';'西天北.txt';'东地北.txt';'西地南.txt';...
'东北天.txt';'西南天.txt';'东南地.txt';'西北地.txt';}; % 12位置
file_num = 9000;
%% 读取数据并计算标定参数矩阵
% 存放12位置的均值
pos = zeros(12,3);
for i =1:12
[pos(i,1),pos(i,2),pos(i,3)] = Acc_mean( file{i}, file_num );
end
acc_ture = [1 1 -1 -1 0 0 0 0 0 0 0 0 ;...
0 0 0 0 1 1 -1 -1 0 0 0 0 ;...
0 0 0 0 0 0 0 0 1 1 -1 -1 ;...
ones(1,12)];
K_a = pos' * acc_ture'* inv(acc_ture * acc_ture');
save("K_a.mat",'K_a')
% 对均值补偿后
acc_x_com = inv(K_a(:,1:3)) * ( pos' - repmat(K_a(:,4), 1, 12)); % 此处可以不用复制,直接利用广播
acc_y_com = inv(K_a(:,1:3)) * ( pos' - repmat(K_a(:,4), 1, 12));
acc_z_com = inv(K_a(:,1:3)) * ( pos' - repmat(K_a(:,4), 1, 12));
%% 绘图 抽取一个位置绘制补偿后的误差图 东北天
ENU = load( file{9} );
t=1:1000;
ENU_com = inv( K_a(:,1:3) ) * ( ENU(t,22:24)' - K_a(:,4) );
figure(1)
plot(t,ENU_com(1,:), 'r', t, ENU(t,22), 'b')
legend('补偿后输出','补偿前输出')
xlabel('数据数目')
ylabel('X轴(g)')
figure(2)
plot(t,ENU_com(2,:), 'r' , t, ENU(t,23), 'b')
legend('补偿后输出','补偿前输出')
xlabel('数据数目')
ylabel('Y轴(g)')
figure(3)
plot(t, ENU_com(3,:), 'r', t, ENU(t,24), 'b')
legend('补偿后输出','补偿前输出')
xlabel('数据数目')
ylabel('Z轴(g)')
function [ax_avr,ay_avr,az_avr] = Acc_mean( file_name, file_num )
% input: file_name 数据文件名 file_num 取文件中数据行数, 相当于设定时间
% output : 加速度均值
data = load( file_name );
ax = data(1:file_num, 22);
ay = data(1:file_num, 23);
az = data(1:file_num, 24);
ax_avr = mean( ax );
ay_avr = mean( ay );
az_avr = mean( az );
2.2 非线性度

此处主要采用了三轴多功能转台,采用位置模式,将惯导的某个轴加速度计置于不同的重力激励下,采集数据,测试非线性。
具体如下:角度值主要要参考惯导的轴向与安装方向。

固定位置采集1min数据求均值。
clear;
close all;
clc;
format compact;
format long g;
% 2021.6 In NJUST by MaYiming
%% 初始化
x_file = {'ax_1.txt';'ax_0.9.txt';'ax_0.7.txt';'ax_0.5.txt';...
'ax_0.3.txt';'ax_0.1.txt';'ax_0.01.txt';}; % 加速度计的数据文件
y_file = {'ay_1.txt';'ay_0.9.txt';'ay_0.7.txt';'ay_0.5.txt';...
'ay_0.3.txt';'ay_0.1.txt';'ay_0.01.txt';}; % 加速度计的数据文件
z_file = {'az_1.txt';'az_0.9.txt';'az_0.7.txt';'az_0.5.txt';...
'az_0.3.txt';'az_0.1.txt';'az_0.01.txt';}; % 加速度计的数据文件
file_num = 3000; % 1min数据
%% 读取数据并计算标定参数矩阵
% 计算 X 轴加速度计
pos = zeros(7,3);
for i =1:7
[pos(i,1),pos(i,2),pos(i,3)] = Acc_mean( x_file{i}, file_num );
end
ax = pos(:,1)';
acc_ture = [1 0.9 0.7 0.5 0.3 0.1 0.01];
kb_x = polyfit(ax, acc_ture, 1); % 实际测量为x, 目标为y
acc_fit_x = kb_x(1)*ax + kb_x(2);
delta_x = abs(acc_fit_x - ax);
NL_x = 2*max(delta_x,[],2)/(1-0.001); % X轴加速度计非线性为NL,没有换算为百分比
% 计算 Y 轴加速度计
pos = zeros(7,3);
for i =1:7
[pos(i,1),pos(i,2),pos(i,3)] = Acc_mean( y_file{i}, file_num );
end
ay = pos(:,2)';
kb_y = polyfit(ay, acc_ture, 1); % 实际测量为x, 目标为y
acc_fit_y = kb_y(1)*ay + kb_y(2);
delta_y = abs(acc_fit_y - ay);
NL_y = 2*max(delta_y,[],2)/(1-0.001); % X轴加速度计非线性为NL,没有换算为百分比
% 计算 Z 轴加速度计
pos = zeros(7,3);
for i =1:7
[pos(i,1),pos(i,2),pos(i,3)] = Acc_mean( z_file{i}, file_num );
end
az = pos(:,3)';
kb_z = polyfit(az, acc_ture, 1); % 实际测量为x, 目标为y
acc_fit_z = kb_z(1)*az + kb_z(2);
delta_z = abs(acc_fit_z - az);
NL_z = 2*max(delta_z,[],2)/(1-0.001); % X轴加速度计非线性为NL,没有换算为百分比
function [ax_avr,ay_avr,az_avr] = Acc_mean( file_name, file_num )
% input: file_name 数据文件名 file_num 取文件中数据行数, 相当于设定时间
% output : 加速度均值
data = load( file_name );
ax = data(1:file_num, 22);
ay = data(1:file_num, 23);
az = data(1:file_num, 24);
ax_avr = mean( ax );
ay_avr = mean( ay );
az_avr = mean( az );
2.3 0/1g稳定性
%% 计算加速度计的稳定性
clc;
clear;
%% 初始值
x_file_name = '天北西0.5h.txt';
y_file_name = '南天西0.5h.txt';
z_file_name = '北西天0.5h.txt';
file_num = 90000;
%% 读取三个轴静态数据
data = load(x_file_name);
x = data(1:file_num, 19); % x轴陀螺仪静态数据 基准轴向上
% 加速度计数据
ax1 = data(1:file_num, 22); % x轴加速度计1g 静态数据
ay0 = data(1:file_num, 23); % y轴加速度计0g 静态数据
az0 = data(1:file_num, 24); % z轴加速度计0g 静态数据
data = load(y_file_name);
y = data(1:file_num, 20); % y轴陀螺仪静态数据 基准轴向上
% 加速度计数据
ay1 = data(1:file_num, 23); % y轴加速度计1g 静态数据
ax0 = data(1:file_num, 22);% x轴加速度计0g 静态数据
data = load(z_file_name);
z = data(1:file_num, 21); % z轴陀螺仪静态数据 基准轴向上
%加速度计数据
az1 = data(1:file_num, 24); % z轴加速度计1g 静态数据
%% 计算三个轴加速度计稳定性
load('K_a.mat')
%% 计算1g稳定性
P = 500; % 平滑
N = 90000; %1800s数据
% 对三轴加速度计数据分段取平均
x_P = zeros(1, N/P);
y_P = zeros(1, N/P);
z_P = zeros(1, N/P);
for i = 1:N/P
x_P(i) = mean( ax1((i-1)*P+1:i*P) );
y_P(i) = mean( ay1((i-1)*P+1:i*P) );
z_P(i) = mean( az1((i-1)*P+1:i*P) );
end
ax1_mean = mean(ax1);
ay1_mean = mean(ay1);
az1_mean = mean(az1);
x1_sigma = (1/K_a(1,1)) *sqrt( sum( ( x_P - ax1_mean ).^2 ) / (N/P - 1) );
y1_sigma = (1/K_a(2,2)) *sqrt( sum( ( y_P - ay1_mean ).^2 ) / (N/P - 1) );
z1_sigma = (1/K_a(3,3)) *sqrt( sum( ( z_P - az1_mean ).^2 ) / (N/P - 1) );
% 计算0g稳定性
x_P = zeros(1, N/P);
y_P = zeros(1, N/P);
z_P = zeros(1, N/P);
for i = 1:N/P
x_P(i) = mean( ax0((i-1)*P+1:i*P) );
y_P(i) = mean( ay0((i-1)*P+1:i*P) );
z_P(i) = mean( az0((i-1)*P+1:i*P) );
end
ax0_mean = mean(ax0);
ay0_mean = mean(ay0);
az0_mean = mean(az0);
x0_sigma = (1/K_a(1,1)) * sqrt( sum( ( x_P - ax0_mean ).^2 ) / (N/P - 1) );
y0_sigma = (1/K_a(2,2)) * sqrt( sum( ( y_P - ay0_mean ).^2 ) / (N/P - 1) );
z0_sigma = (1/K_a(3,3)) * sqrt( sum( ( z_P - az0_mean ).^2 ) / (N/P - 1) );
2.4 阈值、分辨力

加速度计阈值实验:
将加速度计轴向调整到水平位置,调整其水平的俯仰角,从而获得一个加速度的小量。
测试一分钟数据


分辨率:
加速度计:0.5g,0.6g,0.61g,0.611g,0.6111g,变化量分别为0.1g,0.01g,0.001g,0.0001g,只测正值。
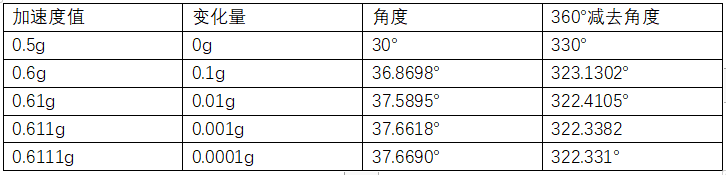
由于阈值和分辨力的测试需要不断调整以获得较为准确的值,因此本文对每个数量级进行测试,结果只精确到数量级。
加速度计阈值与分辨力计算的代码在陀螺仪部分给出。
三、陀螺仪的标定与测试
3.1 标度因数、安装误差以及零偏(偏值)
陀螺仪的标度因数、安装误差以及偏值的测试通常采用正反角速率法。
正负角速率的选择可以参考GB321-2005规定的R5系列,正转与反转的角速率点的选择分别不小于11个点。数据采集时, 小于100°/s的角速率点采集数据不少于30个,大于100°/s的角速率点采集数据不少于5个 (以1s的采样间隔)。
在计算的时候可以考虑去除地球自转分量,地球分量的去除和安装方位以及所处地理纬度有关。
计算模型和过程同加速度计类似,不在赘述(最小二乘)。
clear;
close all;
clc;
format compact;
%% 初始化
%实验室经度118.8533457,纬度32.0292177,高度19.938
% txt数据格式
% 帧计数 wx wy wz ax ay az 从19-24列
% 2021.6 In NJUST by MaYiming
%% xyz轴转动的角速率
rate = [200, 160, 100, 63, 40, 25, 16, 10, 6.3, 4, 2.5, 1.6, 1, -1, -1.6, -2.5, -4, -6.3, -10, -16, -25, -40, -63, -100, -160, -200];
%% x轴旋转
x_file = { 'x_200.txt';'x_160.txt';'x_100.txt';'x_63.txt';'x_40.txt';'x_25.txt';'x_16.txt';'x_10.txt';'x_6.3.txt';'x_4.txt';'x_2.5.txt';
'x_1.6.txt';'x_1.txt';'x_-1.txt';'x_-1.6.txt';'x_-2.5.txt';'x_-4.txt';'x_-6.3.txt';'x_-10.txt';'x_-16.txt';'x_-25.txt';'x_-40.txt';
'x_-63.txt';'x_-100.txt';'x_-160.txt';'x_-200.txt'};
%% y轴旋转
y_file = { 'y_200.txt';'y_160.txt';'y_100.txt';'y_63.txt';'y_40.txt';'y_25.txt';'y_16.txt';'y_10.txt';'y_6.3.txt';'y_4.txt';'y_2.5.txt';
'y_1.6.txt';'y_1.txt';'y_-1.txt';'y_-1.6.txt';'y_-2.5.txt';'y_-4.txt';'y_-6.3.txt';'y_-10.txt';'y_-16.txt';'y_-25.txt';'y_-40.txt';
'y_-63.txt';'y_-100.txt';'y_-160.txt';'y_-200.txt'};
%% z轴旋转
z_file = { 'z_200.txt';'z_160.txt';'z_100.txt';'z_63.txt';'z_40.txt';'z_25.txt';'z_16.txt';'z_10.txt';'z_6.3.txt';'z_4.txt';'z_2.5.txt';
'z_1.6.txt';'z_1.txt';'z_-1.txt';'z_-1.6.txt';'z_-2.5.txt';'z_-4.txt';'z_-6.3.txt';'z_-10.txt';'z_-16.txt';'z_-25.txt';'z_-40.txt';
'z_-63.txt';'z_-100.txt';'z_-160.txt';'z_-200.txt'};
file_num = [450 450 360 600 900 1440 2250 1800 2857 4500 7200 11250 18000 18000 11250 7200 4500 2857 1800 2250 1440 900 600 360 450 450];
%% 绕x轴转动时,三个轴陀螺仪输出的均值
rate_num = length(rate);
x_wx = zeros(1,rate_num);
x_wy = zeros(1,rate_num);
x_wz = zeros(1,rate_num);
for i = 1:rate_num
[x_wx(1,i), x_wy(1,i), x_wz(1,i)] = Gyro_mean( x_file{i}, file_num(i)); % 对应函数read_txt,求陀螺仪三个轴的均值
end
%% y轴旋转,三个轴陀螺仪输出的均值
y_wx = zeros(1,rate_num);
y_wy = zeros(1,rate_num);
y_wz = zeros(1,rate_num);
for i = 1:rate_num
[y_wx(1,i), y_wy(1,i), y_wz(1,i)] = Gyro_mean( y_file{i}, file_num(i) );% 对应函数read_txt,求陀螺仪三个轴的均值
end
%% z轴旋转,三个轴陀螺仪输出的均值
z_wx = zeros(1,rate_num);
z_wy = zeros(1,rate_num);
z_wz = zeros(1,rate_num);
for i = 1:rate_num
[z_wx(1,i), z_wy(1,i), z_wz(1,i)] = Gyro_mean( z_file{i}, file_num(i) );% 对应函数read_txt,求陀螺仪三个轴的均值
end
%% 计算标定参数矩阵
gyro_mean = [x_wx y_wx z_wx; ...
x_wy y_wy z_wy;...
x_wz y_wz z_wz ]; % 3*78
gyro_ture = [rate zeros(1, rate_num * 2);...
zeros(1, rate_num) rate zeros(1, rate_num);...
zeros(1, rate_num*2) rate;... % z轴 转台角速度与惯导角速度相同,所以需要翻转rate向量
ones(1, rate_num*3)]; % 4*78
K_g = gyro_mean * gyro_ture'* inv(gyro_ture * gyro_ture');
save("K_g.mat",'K_g')
%% 对均值补偿
chioce = 1;
if chioce == 0
%直接用广义逆矩阵
gyro_x_com = pinv(K_g) * [x_wx(4:16); x_wy(4:16); x_wz(4:16)];
gyro_y_com = pinv(K_g) * [y_wx(4:16); y_wy(4:16); y_wz(4:16)];
gyro_z_com = pinv(K_g) * [z_wx(4:16); z_wy(4:16); z_wz(4:16)];
else
%分两步 不用广义逆矩阵 取此方法较好
gyro_x_com = inv(K_g(:,1:3)) * ( [x_wx; x_wy ;x_wz ] - repmat( K_g(:,4), 1, rate_num) ); % 此处可以不用复制,直接利用广播
gyro_y_com = inv(K_g(:,1:3)) * ( [y_wx ;y_wy ;y_wz ] - repmat( K_g(:,4), 1, rate_num) );
gyro_z_com = inv(K_g(:,1:3)) * ( [z_wx ;z_wy ;z_wz ] - repmat( K_g(:,4), 1, rate_num) );
end
%% 标度因数非线性度
K_m = zeros(3,26);
for i = 1:26
K_m(1,i) = abs(gyro_x_com(1,i) - x_wx(i))/(K_g(1,1)*400);
K_m(2,i) = abs(gyro_y_com(2,i) - y_wy(i))/(K_g(2,2)*400);
K_m(3,i) = abs(gyro_z_com(3,i) - z_wz(i))/(K_g(3,3)*400);
end
Km = max(K_m,[],2);
%% 标度因数不对称度
gyro_mean_positive = [x_wx(1:13) y_wx(1:13) z_wx(1:13); ...
x_wy(1:13) y_wy(1:13) z_wy(1:13);...
x_wz(1:13) y_wz(1:13) z_wz(1:13) ];
gyro_mean_negative = [x_wx(14:26) y_wx(14:26) z_wx(14:26); ...
x_wy(14:26) y_wy(14:26) z_wy(14:26);...
x_wz(14:26) y_wz(14:26) z_wz(14:26) ];
gyro_ture_positive = [rate(1:13) zeros(1, 26);...
zeros(1, 13) rate(1:13) zeros(1, 13);...
zeros(1, 26) rate(1:13);...
ones(1, 39)];
gyro_ture_negative = [rate(1,14:26) zeros(1, 26 );...
zeros(1, 13) rate(1,14:26) zeros(1, 13);...
zeros(1, 26) rate(1,14:26);...
ones(1, 39)];
K_g_positive = gyro_mean_positive * gyro_ture_positive'* inv(gyro_ture_positive * gyro_ture_positive');
K_g_negative = gyro_mean_negative * gyro_ture_negative'* inv(gyro_ture_negative * gyro_ture_negative');
K_mu = abs(diag(K_g_positive(:,1:3)) - diag(K_g_negative(:,1:3)))./((diag(K_g_positive(:,1:3)) + diag(K_g_negative(:,1:3)))/2);
%% figure 绘制三个轴分别旋转时 三轴的补偿效果
x = load('x_4.txt');
y = load('y_4.txt');
z = load('z_4.txt');
t = 1:1000;
x_gyro = x(1:1000,19:21)';
y_gyro = y(1:1000,19:21)';
z_gyro = z(1:1000,19:21)';
x_gyro_com = inv(K_g(:,1:3)) * ( x_gyro - K_g(:,4) );
y_gyro_com = inv(K_g(:,1:3)) * ( y_gyro - K_g(:,4) );
z_gyro_com = inv(K_g(:,1:3)) * ( z_gyro - K_g(:,4) );
figure(1)
plot(t,x_gyro(1,:),'b',t,x_gyro_com(1,:),'r')
legend('补偿前输出','补偿后输出')
ylabel('陀螺输出')
xlabel('数据数目')
figure(2)
plot(t,x_gyro(2,:),'b',t,x_gyro_com(2,:),'r')
legend('补偿前输出','补偿后输出')
ylabel('陀螺输出')
xlabel('数据数目')
figure(3)
plot(t,x_gyro(3,:),'b',t,x_gyro_com(3,:),'r')
legend('补偿前输出','补偿后输出')
ylabel('陀螺输出')
xlabel('数据数目')
figure(4)
plot(t,y_gyro(1,:),'b',t,y_gyro_com(1,:),'r')
legend('补偿前输出','补偿后输出')
ylabel('陀螺输出')
xlabel('数据数目')
figure(5)
plot(t,y_gyro(2,:),'b',t,y_gyro_com(2,:),'r')
legend('补偿前输出','补偿后输出')
ylabel('陀螺输出')
xlabel('数据数目')
figure(6)
plot(t,y_gyro(3,:),'b',t,y_gyro_com(3,:),'r')
legend('补偿前输出','补偿后输出')
ylabel('陀螺输出')
xlabel('数据数目')
figure(7)
plot(t,z_gyro(1,:),'b',t,z_gyro_com(1,:),'r')
legend('补偿前输出','补偿后输出')
ylabel('陀螺输出')
xlabel('数据数目')
figure(8)
plot(t,z_gyro(2,:),'b',t,z_gyro_com(2,:),'r')
legend('补偿前输出','补偿后输出')
ylabel('陀螺输出')
xlabel('数据数目')
figure(9)
plot(t,z_gyro(3,:),'b',t,z_gyro_com(3,:),'r')
legend('补偿前输出','补偿后输出')
ylabel('陀螺输出')
xlabel('数据数目')
% txt数据格式
% 帧计数 wx wy wz ax ay az 从19-24列
% 2021.6 In NJUST by MaYiming
function [wx_avr,wy_avr,wz_avr] = Gyro_mean( file_name, file_num )
% input: 数据文件名
% output : 角速度均值
x = load( file_name );
wx = x(1:file_num, 19);
wy = x(1:file_num, 20);
wz =x(1:file_num, 21);
wx_avr = mean( wx );
wy_avr = mean( wy );
wz_avr =mean( wz );
3.2标度因数不对称性、非线性:
该部分代码见3.1代码
3.3 零偏与零偏稳定性

此处零偏取了30min的数据求取了均值,具体时间可以根据用户设定。

此处零偏稳定性取10s平滑,即10s数据平均周期,该值对零偏稳定性影响较大,一般取的越小得到的数值越大,反之同理。
%% 计算陀螺仪零偏与零偏稳定性
% 2021.6 In NJUST by MaYiming
clc;
clear;
%% 初始值
x_file_name = '天北西0.5h.txt';
y_file_name = '南天西0.5h.txt';
z_file_name = '北西天0.5h.txt';
file_num = 90000;
% 读取三轴陀螺仪数据
data = load(x_file_name);
x = data(1:file_num, 19); % x轴陀螺仪静态数据 基准轴向上
data = load(y_file_name);
y = data(1:file_num, 20); % y轴陀螺仪静态数据 基准轴向上
data = load(z_file_name);
z = data(1:file_num, 21); % z轴陀螺仪静态数据 基准轴向上
%% 计算
load('K_g.mat')
x_mean = mean(x);
y_mean = mean(y);
z_mean = mean(z);
%计算三轴陀螺仪的零偏
x_B0 = ( 1/K_g(1,1) ) * x_mean;
y_B0 = ( 1/K_g(2,2) ) * y_mean;
z_B0 = ( 1/K_g(3,3) ) * z_mean;
%补偿地球自转
we = 15/3600; % °/s
x_B0 = x_B0 - we*sind(32);
y_B0 = y_B0 - we*sind(32);
z_B0 = z_B0 - we*sind(32);
%% 零偏稳定性计算
P = 500; % 10s平滑
N = 90000; %1800s数据
% 对三轴陀螺仪数据分段取平均
x_P = zeros(1, N/P);
y_P = zeros(1, N/P);
z_P = zeros(1, N/P);
for i = 1:N/P
x_P(i) = mean( x((i-1)*P+1:i*P) );
y_P(i) = mean( y((i-1)*P+1:i*P) );
z_P(i) = mean( z((i-1)*P+1:i*P) );
end
x_Bsm = ( 1/K_g(1,1) ) * sqrt( ( 1 / (N/P-1) ) * sum( (x_P - x_B0).^2 ) );
y_Bsm = ( 1/K_g(2,2) ) * sqrt( ( 1 / (N/P-1) ) * sum( (y_P - y_B0).^2 ) );
z_Bsm = ( 1/K_g(3,3) ) * sqrt( ( 1 / (N/P-1) ) * sum( (z_P - z_B0).^2 ) );
x_Bsm*3600 % 从°/s到°/h
y_Bsm*3600
z_Bsm*3600
3.4 阈值与分辨力

阈值测试过程与加速度计类似。
陀螺仪阈值实验:
X轴:正负1°/s,0.5°/s,0.1°/s,0.05°/s,0.01°/s
Y轴:正负0.1°/s,0.05°/s,0.01°/s,0.001°/s
Z轴:正负0.1°/s,0.05°/s,0.01°/s,0.001°/s
% 2021.6 In NJUST by MaYiming
clc;
clear;
%% 计算阈值
load('K_g.mat')
load('K_a.mat')
file_num = 50; % 1s计算
%% 定义参数
file_name = 'az_0.01.txt';
rate = [0;0;0.01]; % 真实转速 或者 真实加速度
flag = 2; %0为测x轴,1为y轴,2为z轴
flag_m = 1; % 0为陀螺仪 1为加速度计
if flag_m == 0
%% 陀螺仪的阈值计算
thresholds = zeros(1,60);
for i = 1:60
[wx, wy, wz] = Gyro_mean_zone( file_name, (i-1) * file_num + 1, i * file_num );
com = K_g(:,1:3) * rate ;
if flag == 2
[kx0, ky0, kz0] = Gyro_mean('z_0.txt',9000);
threshold = abs(wz - kz0 - com(3))/com(3);
elseif flag == 1
[kx0, ky0, kz0] = Gyro_mean('y_0.txt',9000);
threshold = abs(wy - ky0 - com(2))/com(2);
else
[kx0, ky0, kz0] = Gyro_mean('x_0.txt',9000);
threshold = abs(wx - kx0 - com(1))/com(1);
end
thresholds(i) = threshold ;
end
%% 加速度计的阈值计算
else
thresholds = zeros(1,60);
for i = 1:60
[ax, ay, az] = Acc_mean_zone( file_name, (i-1) * file_num + 1, i * file_num );
com = K_a(:,1:3) * rate ;
if flag == 2
[kx0, ky0, kz0] = Gyro_mean('az_0.txt',9000);
threshold = abs(az - kz0 - com(3))/com(3);
elseif flag == 1
[kx0, ky0, kz0] = Gyro_mean('ay_0.txt',9000);
threshold = abs(ay - ky0 - com(2))/com(2);
else
[kx0, ky0, kz0] = Gyro_mean('ax_0.txt',9000);
threshold = abs(ax - kx0 - com(1))/com(1);
end
thresholds(i) = threshold ;
end
end
% txt数据格式
% 帧计数 wx wy wz ax ay az 从19-24列
% 2021.6 In NJUST by MaYiming
function [wx_avr,wy_avr,wz_avr] = Gyro_mean_zone( file_name, file_start, file_end )
% input: 数据文件名
% output : 角速度均值
x = load( file_name );
wx = x(file_start:file_end, 19);
wy = x(file_start:file_end, 20);
wz =x(file_start:file_end, 21);
wx_avr = mean( wx );
wy_avr = mean( wy );
wz_avr =mean( wz );
% txt数据格式
% 帧计数 wx wy wz ax ay az 从19-24列
% 2021.6 In NJUST by MaYiming
function [wx_avr,wy_avr,wz_avr] = Gyro_mean( file_name, file_num )
% input: 数据文件名
% output : 角速度均值
x = load( file_name );
wx = x(1:file_num, 19);
wy = x(1:file_num, 20);
wz =x(1:file_num, 21);
wx_avr = mean( wx );
wy_avr = mean( wy );
wz_avr =mean( wz );
% txt数据格式
% 帧计数 wx wy wz ax ay az 从19-24列
% 2021.6 In NJUST by MaYiming
function [ax_avr,ay_avr,az_avr] = Acc_mean_zone( file_name, file_start, file_end )
% input: file_name 数据文件名 file_num 取文件中数据行数, 相当于设定时间
% output : 加速度均值
data = load( file_name );
ax = data(file_start:file_end, 22);
ay = data(file_start:file_end, 23);
az = data(file_start:file_end, 24);
ax_avr = mean( ax );
ay_avr = mean( ay );
az_avr = mean( az );
% txt数据格式
% 帧计数 wx wy wz ax ay az 从19-24列
% 2021.6 In NJUST by MaYiming
function [ax_avr,ay_avr,az_avr] = Acc_mean( file_name, file_num )
% input: file_name 数据文件名 file_num 取文件中数据行数, 相当于设定时间
% output : 加速度均值
data = load( file_name );
ax = data(1:file_num, 22);
ay = data(1:file_num, 23);
az = data(1:file_num, 24);
ax_avr = mean( ax );
ay_avr = mean( ay );
az_avr = mean( az );
clc;
clear;
%% 分辨力计算
% 2021.6 In NJUST by MaYiming
file_num = 50;
load('K_g.mat')
load('K_a.mat')
%% 定义参数
file_name_before = 'z_-0.4.txt'; % 前一步文件名
file_name_after = 'z_-0.41.txt'; %下一步文件名
delta_rate = [0;0;0.01]; % 差值
flag = 2; %0为测x轴,1为y轴,2为z轴
flag_m = 0; % 0为陀螺仪 1为加速度计
if flag_m == 0
%% 陀螺仪的分辨力计算
resolutions = zeros(1,60);
for i = 1:60
[wx_b, wy_b, wz_b] = Gyro_mean_zone( file_name_before, (i-1) * file_num + 1, i * file_num );
[wx_a, wy_a, wz_a] = Gyro_mean_zone( file_name_after, (i-1) * file_num + 1, i * file_num );
delta_com = K_g(:,1:3) * delta_rate ;
if flag == 2
delta = abs(wz_a - wz_b);
res = (delta - delta_com(3)) / delta_com(3);
elseif flag == 1
delta = abs(wy_a - wy_b);
res = (delta - delta_com(2)) / delta_com(2);
else
delta = abs(wx_a - wx_b);
res = (delta - delta_com(1)) / delta_com(1);
end
resolutions(i) = res;
end
%% 加速度计的分辨率计算
else
resolutions = zeros(1,60);
for i = 1 :60
[ax_b, ay_b, az_b] = Acc_mean_zone( file_name_before, (i-1) * file_num + 1, i * file_num );Acc_mean( file_name_before, file_num );
[ax_a, ay_a, az_a] = Acc_mean_zone( file_name_after, (i-1) * file_num + 1, i * file_num );
delta_com = K_a(:,1:3) * delta_rate ;
if flag == 2
delta = abs(az_a - az_b);
res = (delta - delta_com(3)) / delta_com(3);
elseif flag == 1
delta = abs(ay_a - ay_b);
res = (delta - delta_com(2)) / delta_com(2);
else
delta = abs(ax_a - ax_b);
res = (delta - delta_com(1)) / delta_com(1);
end
resolutions(i) = res;
end
end
所用到的函数同上。
3.5 ALLAN方差
具体理论参阅相关论文。


一般而言ALLAN方差的测试需要在大理石台上静置,不应该放在动基座上,放在动基座上会附加动基座的静态特性,测出来不准确。
MEMS惯导的ALLAN测试通常需要进行数小时甚至数十小时。
clc;
clear;
% 帧计数 wx wy wz ax ay az 从19-24列
% 2021.6 In NJUST by MaYiming
%% 严恭敏函数 计算allan方差
data = load('天北西7h.txt');
file_num = 6.5*3600*50; % 6h
x = data(1:file_num,19);
y = data(1:file_num,20);
z = data(1:file_num,21);
[x_sigma, x_tau, x_Err] = avar(x, 0.02); % sigma是标准差,不是allan方差
[y_sigma, y_tau, y_Err] = avar(y, 0.02);
[z_sigma, z_tau, z_Err] = avar(z, 0.02);
% %% MATLAB计算 三个轴陀螺仪艾伦方差
% % 目前有 x y z 为三轴陀螺仪数据 ax1 ay1 az1为1g加速度计静态数据 ax0 ay0 az0 为0g加速度计数据
% m = 2.^(0:19); % 平均取样因子
% Fs = 50; % 50HZ
%
% [x_avar,x_tau] = allanvar(x,m,Fs);
% [y_avar,y_tau] = allanvar(y,m,Fs);
% [z_avar,z_tau] = allanvar(z,m,Fs);poly
%% 计算各项系数
x0 = [0;0;0;0;0]; % 最小二乘法初始迭代值
fun = @(co,xdata)co(1)*xdata.^(-2)+co(2)*xdata.^(-1)+co(3)+co(4)*xdata.^(1)+co(5)*xdata.^(2); % 拟合的函数
co_x = abs( lsqcurvefit(fun, x0, x_tau, x_sigma.^2) ); %这里拟合的为方差,如果是标准差的话需要调整fun。
co_y = abs( lsqcurvefit(fun, x0, y_tau, y_sigma.^2) );
co_z = abs( lsqcurvefit(fun, x0, z_tau, z_sigma.^2) );
x_random_cof = [sqrt(co_x(1)/3)*1e6*3.141592653/180 sqrt(co_x(2))*60 sqrt(co_x(3))*1.5*3600 sqrt(co_x(4)*3)*60*3600 sqrt(co_x(5)*2)*3600*3600];
y_random_cof = [sqrt(co_y(1)/3)*1e6*3.141592653/180 sqrt(co_y(2))*60 sqrt(co_y(3))*1.5*3600 sqrt(co_y(4)*3)*60*3600 sqrt(co_y(5)*2)*3600*3600];
z_random_cof = [sqrt(co_z(1)/3)*1e6*3.141592653/180 sqrt(co_z(2))*60 sqrt(co_z(3))*1.5*3600 sqrt(co_z(4)*3)*60*3600 sqrt(co_z(5)*2)*3600*3600];
function [sigma, tau, Err] = avar(y0, tau0)
% 计算Allan方差
% 输入:y -- 数据(一行或列向量), tau0 -- 采样周期
% 输出:sigma -- Allan方差(量纲单位与输入y保持一致), tau -- 取样时间, Err -- 百分比估计误差
% 作者: Yan Gong-min, 2012-08-22
% example:
% y = randn(100000,1) + 0.00001*[1:100000]';
% [sigma, tau, Err] = avar(y, 0.1);
N = length(y0);
y = y0; NL = N;
for k = 1:inf
sigma(k,1) = sqrt(1/(2*(NL-1))*sum([y(2:NL)-y(1:NL-1)].^2));
tau(k,1) = 2^(k-1)*tau0;
Err(k,1) = 1/sqrt(2*(NL-1));
NL = floor(NL/2);
if NL<3
break;
end
y = 1/2*(y(1:2:2*NL) + y(2:2:2*NL)); % 分组长度加倍(数据长度减半)
end
subplot(211), plot(tau0*[1:N], y0); grid
xlabel('\itt \rm/ s'); ylabel('\ity');
subplot(212),
loglog(tau, sigma, '-+', tau, [sigma.*(1+Err),sigma.*(1-Err)], 'r--'); grid
xlabel('\itt \rm/ s'); ylabel('\it\sigma_A\rm( \tau )');
上述理论部分可以参阅严恭敏《惯性仪器测试与数据分析》,以及惯导标定相关的硕士论文。