硬件语言Verilog HDL牛客刷题day11 A里部分 和 Z兴部分
1.VL72 全加器
1.题目:
① 请用题目提供的半加器实现全加器电路①
半加器的参考代码如下,可在答案中添加并例化此代码。
2. 解题思路 (可以看代码)
2.1 先看 半加器 s 是加位 , C 是进位。
2.2 再看全加器 s 是加位 , C 是进位。
2.3 解题办法一 , 直接assign 不使用 半加器。
2.4 解题办法二, 直接assign 使用 半加器,两个相加得出 加位, assign 得出 进位。
3. 解题代码
`timescale 1ns/1ns
module add_half(
input A ,
input B ,
output wire S ,
output wire C
);
assign S = A ^ B;
assign C = A & B;
endmodule
/***************************************************************/
module add_full(
input A ,
input B ,
input Ci ,
output wire S ,
output wire Co
);
assign S = A ^ B ^ Ci;
assign Co = (A & B) | (B & Ci);
/*
wire c_1;
wire c_2;
wire sum_1;
add_half add_half_1(
.A (A),
.B (B),
.S (sum_1),
.C (c_1)
);
add_half add_half_2(
.A (sum_1),
.B (Ci),
.S (S),
.C (c_2)
);
assign Co = c_1 | c_2;
*/
endmodule2.VL73 串行进位加法器
1.题目:
② 请用全加器电路①实现串行进位的4位全加器电路
1位全加器参考代码如下
module add_half(
input A ,
input B ,
output wire S ,
output wire C
);
assign S = A ^ B;
assign C = A & B;
endmodule
/***************************************************************/
module add_full(
input A ,
input B ,
input Ci ,
output wire S ,
output wire Co
);
wire c_1;
wire c_2;
wire sum_1;
add_half add_half_1(
.A (A),
.B (B),
.S (sum_1),
.C (c_1)
);
add_half add_half_2(
.A (sum_1),
.B (Ci),
.S (S),
.C (c_2)
);
assign Co = c_1 | c_2;
endmodule2.解题思路
2.1 四位得加法器
2.2 C0 两个四位数据得 进位, S[3:0] 两个数据得加位。
2.3 按照数据的位置加就行了, (分成四位)。
3.解题代码
`timescale 1ns/1ns
module add_4(
input [3:0] A ,
input [3:0] B ,
input Ci ,
output wire [3:0] S ,
output wire Co
);
wire s1[4:0];
wire c1[4:0];
add_full U1(
.A (A[0]),
.B (B[0]),
.Ci (Ci),
.S (s1[0]),
.Co (c1[0])
);
add_full U2(
.A (A[1]),
.B (B[1]),
.Ci (c1[0]),
.S (s1[1]),
.Co (c1[1])
);
add_full U3(
.A (A[2]),
.B (B[2]),
.Ci (c1[1]),
.S (s1[2]),
.Co (c1[2])
);
add_full U4(
.A (A[3]),
.B (B[3]),
.Ci (c1[2]),
.S (s1[3]),
.Co (Co)
);
assign S[0] = s1[0];
assign S[1] = s1[1];
assign S[2] = s1[2];
assign S[3] = s1[3];
endmodule
module add_half(
input A ,
input B ,
output wire S ,
output wire C
);
assign S = A ^ B;
assign C = A & B;
endmodule
/***************************************************************/
module add_full(
input A ,
input B ,
input Ci ,
output wire S ,
output wire Co
);
wire c_1;
wire c_2;
wire sum_1;
add_half add_half_1(
.A (A),
.B (B),
.S (sum_1),
.C (c_1)
);
add_half add_half_2(
.A (sum_1),
.B (Ci),
.S (S),
.C (c_2)
);
assign Co = c_1 | c_2;
endmodule
3.VL74 异步复位同步释放
1.题目:
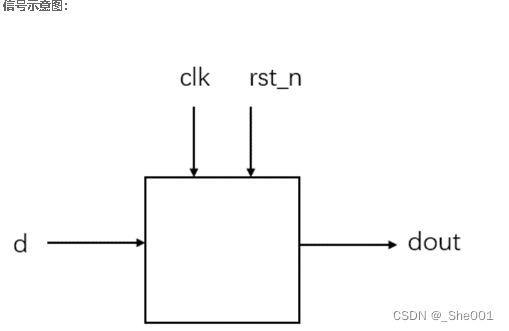
请使用异步复位同步释放来将输入数据a存储到寄存器中,并画图说明异步复位同步释放的机制原理
2.解题思路
2.1 了解 异步复位。
2.2 了解 同步释放
2.3 了解需求。
2.4 观看时序图, 了解 同步时序的两个节拍。
 链接:(29条消息) 异步复位,同步释放_异步复位同步释放_三岁囍的博客-CSDN博客
链接:(29条消息) 异步复位,同步释放_异步复位同步释放_三岁囍的博客-CSDN博客
异步复位、同步释放是指复位信号产生时不受时钟信号的控制,但是释放的时候受到时钟信号的同步。主要目的是防止复位信号释放时候产生亚稳态。
异步复位:当复位信号拉低时,直接进入复位状态。
同步释放:当复位信号释放时,加入两级同步缓存器,电路不会立即释放,而是同步到时钟有效时再进行释放。
3.解题代码
`timescale 1ns/1ns
module ali16(
input clk,
input rst_n,
input d,
output reg dout
);
reg rstn_reg, rstn_reg_1;
//异步复位,同步释放
always @(posedge clk, negedge rst_n) begin
if(!rst_n) begin
rstn_reg <= 1'b0;
rstn_reg_1 <= 1'b0;
end
else begin
rstn_reg <= rst_n;
rstn_reg_1 <= rstn_reg;
end
end
//同步释放
// always @(posedge clk) begin
// rstn_reg_1 <= rstn_reg;
// end
//赋值
always @(posedge clk, negedge rstn_reg_1) begin
if(!rstn_reg_1) begin
dout <= 1'b0;
end
else
dout <= d;
end
endmodule
4.VL75 求最小公倍数
1.题目
设计一个时序电路,输入2个无符号数,位宽可以通过参数DATA_W确定,输出这两个数的最小公倍数和最大公约数。
2.解题思路
2.1 首先 最大公约数的求法:辗转相除法, 相减法,穷举法。 (建议采用 相减法,辗转相除法在有 被除数为 0 的时候很尴尬)
2.1 最小公倍数 的求法是 : 两个数相乘,除去最大公约数。
2.3 注意时序, (我的时序,最大公约的时候开始的时候错误)
2.4 主要看代码 (不要注意题目测试的对错)
3. 解题代码:
过关的: (相减法)
`timescale 1ns/1ns
module lcm#(
parameter DATA_W = 8)
(
input [DATA_W-1:0] A,
input [DATA_W-1:0] B,
input vld_in,
input rst_n,
input clk,
output wire [DATA_W*2-1:0] lcm_out,
output wire [DATA_W-1:0] mcd_out,
output reg vld_out
);
reg [DATA_W*2-1:0] mcd,a_buf,b_buf;
reg [DATA_W*2-1:0] mul_buf;
reg mcd_vld;
reg [1:0] cur_st,nxt_st;
parameter IDLE= 2'b00,S0 = 2'b01, S1 = 2'b10, S2 = 2'b11;
//两段式状态机
always @(posedge clk or negedge rst_n)
if (!rst_n)
cur_st <= IDLE;
else
cur_st <= nxt_st;
always @(posedge clk or negedge rst_n)
if (!rst_n) begin
nxt_st <= IDLE;
mcd <= 0;
mcd_vld <= 0;
a_buf <= 0;
b_buf <= 0;
mul_buf <= 0;
vld_out <= 1'b0;
end
else begin
case (cur_st)
IDLE:if(vld_in) begin
a_buf <= A;
b_buf <= B;
nxt_st <= S0;
mul_buf <= A*B;
mcd_vld <= 0;
vld_out <= 1'b0;
end
else begin
nxt_st <= IDLE;
mcd_vld <= 0;
vld_out <= 1'b0;
end
S0:if(a_buf!=b_buf)begin
if(a_buf>b_buf)begin
a_buf<=a_buf-b_buf;
b_buf<=b_buf;
end
else begin
b_buf <= b_buf - a_buf;
a_buf <= a_buf;
vld_out <= 1'b0;
end
nxt_st <= S0;
end
else begin
nxt_st <=S1;
vld_out <= 1'b0;
end
S1:begin
mcd <= b_buf;
mcd_vld <= 1'b1;
nxt_st <= IDLE;
vld_out <= 1'b1;
end
default:begin
nxt_st<=IDLE;
vld_out <= 1'b0;
end
endcase
end
assign mcd_out = mcd;
assign lcm_out = mul_buf/mcd;
endmodule辗转相除法: (我感觉这个可以的, 只是开始的最大公约数的时序不对)
`timescale 1ns/1ns
module lcm#(
parameter DATA_W = 8)
(
input [DATA_W-1:0] A,
input [DATA_W-1:0] B,
input vld_in,
input rst_n,
input clk,
output wire [DATA_W*2-1:0] lcm_out,
output wire [DATA_W-1:0] mcd_out,
output reg vld_out
);
reg [DATA_W-1:0] a_r;
reg [DATA_W-1:0] b_r;
wire [DATA_W-1:0] a_w;
wire [DATA_W-1:0] b_w;
wire [DATA_W-1:0] res_w;
reg flag_r;
reg [DATA_W*2-1:0] lcm_out_r;
assign vld_out = flag_r && (a_r == b_r);
assign res_w = a_r - b_r;
assign {a_w, b_w} = res_w > b_r ? {res_w, b_r} : {b_r, res_w};
assign mcd_out = vld_out ? a_r : 'd0;
assign lcm_out = lcm_out_r/ mcd_out;
always @(posedge clk or negedge rst_n) begin
if (!rst_n) begin
a_r <= 'd0;
b_r <= 'd0;
flag_r <= 'd0;
end
else if (vld_in) begin
{a_r, b_r} <= A > B ? {A, B} : {B, A};
lcm_out_r <= A * B;
flag_r <= 'd1;
end
else if (vld_out) begin
flag_r <= 'd0;
end
else if (flag_r) begin
a_r <= a_w;
b_r <= b_w;
end
end
endmodule
简单版的 相减法 (没有注意时序)
`timescale 1ns/1ns
module lcm#(
parameter DATA_W = 8)
(
input [DATA_W-1:0] A,
input [DATA_W-1:0] B,
input vld_in,
input rst_n,
input clk,
output wire [DATA_W*2-1:0] lcm_out,
output wire [DATA_W-1:0] mcd_out,
output reg vld_out
);
//gcd
reg [DATA_W-1:0] tmp_m,tmp_n,reg_b,reg_s,mcd_out_r;
reg [DATA_W*2-1:0] lcm_out_r;
reg flag;
always@(posedge clk or negedge rst_n) begin
if(!rst_n) begin
reg_b <= 0;
reg_s <= 0;
vld_out <= 0;
lcm_out_r <= 0;
mcd_out_r <= 0;
flag <= 0;
end
else if(vld_in && A>B) begin
reg_b <= A;
reg_s <= B;
flag <= 1;
end
else if(vld_in) begin
reg_b <= B;
reg_s <= A;
flag <= 1;
end
else if(reg_b % reg_s != 0) begin
reg_b <= reg_s;
reg_s <= reg_b % reg_s;
end
else if(reg_b % reg_s == 0 && flag == 1) begin
vld_out <= 1;
mcd_out_r <= reg_s;
lcm_out_r <= tmp_m * tmp_n / reg_s;
flag <= 0;
end
else begin
vld_out <= 0;
mcd_out_r <= 0;
lcm_out_r <= 0;
end
end
always@(posedge clk or negedge rst_n) begin
if(!rst_n) begin
tmp_m <= 0;
tmp_n <= 0;
end
else if(vld_in) begin
tmp_m <= A;
tmp_n <= B;
end
end
assign mcd_out = mcd_out_r;
assign lcm_out = lcm_out_r;
endmodule
5.VL76 任意奇数倍时钟分频 (这个题,有一点细节)
1.题目:
编写一个模块,对输入的时钟信号clk_in,实现任意奇数分频,要求分频之后的时钟信号占空比为50%。模块应包含一个参数,用于指定分频的倍数。
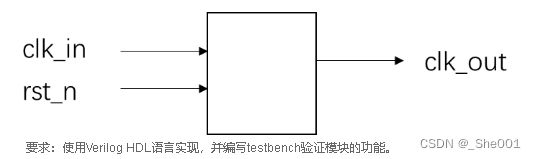
模块的接口信号图如下:
2.解题思路
2.1 首先是 奇数的时钟分频。
2.2 开始的时候我们需要计数, 计数的大小为 n 个周期。
2.3 我们奇数的分频应该是 在其中一个周期 下降沿的时候开始下降。
2.4 可以这样说 开始的时候 cnt =2 上升延变化, 4 个版周期。外加一个 下降沿的 周期的1 等于5 看图:
3.解题代码
`timescale 1ns/1ns
module clk_divider
#(parameter dividor = 5)
( input clk_in,
input rst_n,
output clk_out
);
reg [$clog2(dividor):0] cnt1;
reg clk1, clk2;
always @ (posedge clk_in, negedge rst_n) begin
if(!rst_n) begin
cnt1 <= 0;
end
else if(cnt1 == dividor-1) begin
cnt1 <= 0;
end
else begin
cnt1 <= cnt1 + 1;
end
end
always @ (posedge clk_in, negedge rst_n)begin
if(!rst_n) begin
clk1 <= 1'b0;
end
else if(cnt1 == (dividor - 1)>>1) begin
clk1 <= ~clk1;
end
else if (cnt1 == (dividor-1)) begin
clk1 <= ~clk1;
end
else begin
clk1 <= clk1;
end
end
always @ (negedge clk_in, negedge rst_n)begin
if(!rst_n) begin
clk2 <= 1'b0;
end
else if(cnt1 == (dividor - 1)>>1) begin
clk2 <= ~clk2;
end
else if (cnt1 == (dividor-1)) begin
clk2 <= ~clk2;
end
else begin
clk2 <= clk2;
end
end
assign clk_out = clk1 || clk2; //(4+1 == 5)
endmodule
6.VL77 编写乘法器求解算法表达式
1.题目:
编写一个4bit乘法器模块,并例化该乘法器求解c=12*a+5*b,其中输入信号a,b为4bit无符号数,c为输出。注意请不要直接使用*符号实现乘法功能。
2.解题代码
`timescale 1ns/1ns
module calculation(
input clk,
input rst_n,
input [3:0] a,
input [3:0] b,
output reg [8:0] c
);
reg[8:0]c1;
always@(posedge clk or negedge rst_n)
begin
if(~rst_n)
begin
c1<=0;
end
else
begin
c1 <= 4'd12 * a + 3'd5 * b;
end
end
always@(posedge clk or negedge rst_n)
begin
if(~rst_n)
begin
c<=0;
end
else
begin
c <=c1;
end
end
/*
reg [8:0] a_tmp;
reg [8:0] b_tmp;
reg [8:0] c_tmp;
always@(posedge clk or negedge rst_n)begin
if(!rst_n)begin
a_tmp <= 0;
b_tmp <= 0;
c_tmp <= 0;
end
else begin
a_tmp <= (a << 3) + (a << 2);
b_tmp <= (b << 2) + b;
c_tmp <= a_tmp + b_tmp;
end
end
assign c = c_tmp;
*/
endmodule