《图算法》第四章 路径查找和图搜索算法-2

对图算法有兴趣的朋友可以关注微信公众号 ：《 Medical与AI的故事》

原文链接：《图算法》第四章-2 路径查找和图搜索算法

最短路径变体：A*

A*最短路径算法改进Dijkstra的算法，它更快一些，因为它在确定下一个探索路径时可用的额外信息都包含进来，将这些额外信息作为启发式函数的一部分。

该算法由Peter Hart、Nils Nilsson和Bertram Raphael发明，并在1968年的论文“A Formal Basis for the Heuristic Determination of Minimum Cost Paths”中进行了描述。

在其核心循环的每次迭代中，A*算法都要决定哪个子路径要展开往下探索。这样做是基于对到达目标节点的成本的启发式估计。

在应用了估计路径成本的启发式方法中要考虑周全。如果启发算法低估了路径成本，可能多余地包括了一些可能应当被消除的路径，但结果仍然是准确的。但是，如果启发式方法高估了路径成本，它可能会跳过实际的较短路径（错误地估计为较长路径），而这些路径实际上应当被评估和遍历，这就可能导致不准确的结果。
A*选择能够最小化以下函数的路径：
f(n) = g(n) + h(n)
在这个函数中，

• g(n) 是从起点到节点n的路径成本。
• h(n) 是从节点n到目标节点的路径的估计成本，是在启发计算的结果。
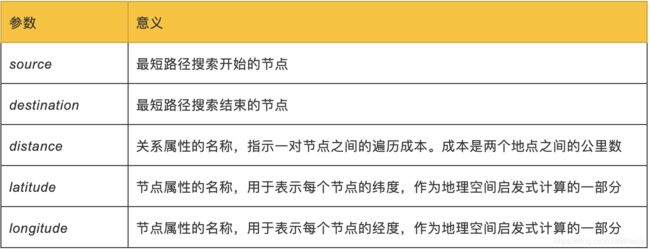
  在Neo4j的实现中，地理空间距离（中间点到目标点的物理空间距离）被用作启发。在我们的示例交通数据集中，我们使用每个位置的纬度和经度作为启发式函数的输入。

Neo4j上的A*算法

以下查询执行A*算法，以查找Den Haag和London之间的最短路径：

MATCH (source:Place {id: "Den Haag"}),
(destination:Place {id: "London"})
CALL algo.shortestPath.astar.stream(source,
destination, "distance", "latitude", "longitude")
YIELD nodeId, cost
RETURN algo.getNodeById(nodeId).id AS place, cost

传递给此算法的参数为：

结果如下：

+----------------------------+
| place              | cost  |
+----------------------------+
| "Den Haag"         | 0.0   |
| "Hoek van Holland" | 27.0  |
| "Felixstowe"       | 234.0 |
| "Ipswich"          | 256.0 |
| "Colchester"       | 288.0 |
| "London"           | 394.0 |
+----------------------------+

使用最短路径算法（无变体）将得到相同的结果，但在更复杂的数据集上，A*算法将更快，因为它评估的路径更少。

最短路径变体：Yen’s K-最短路径

Yen’s k-最短路径算法与最短路径算法相似，但它不只是在两对节点之间找到最短路径，而是计算最短路径的第二最短路径、第三最短路径等，最多可得到k-1种不同的路径。

Jin Y. Yen于1971年发明了该算法，并将其描述为“Finding the K Shortest Loopless Paths in a Network”。该算法在寻找绝对的最短路径并非我们唯一目标时，会有助于找到替代的路径。当我们需要多个备份计划时，它会特别有用！

Neo4j上的Yen’s算法

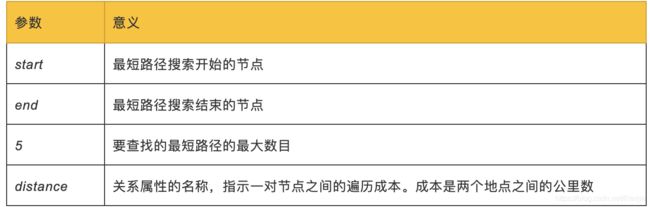
以下查询执行Yen’s算法，以查找Gouda和Felixstowe之间的最短路径：

MATCH (start:Place {id:"Gouda"}),
(end:Place {id:"Felixstowe"})
CALL algo.kShortestPaths.stream(start, end, 5, "distance")
YIELD index, nodeIds, path, costs
RETURN index,
[node in algo.getNodesById(nodeIds[1..-1]) | node.id] AS via,
reduce(acc=0.0, cost in costs | acc + cost) AS totalCost

传递给此算法的参数为：

在返回最短路径之后，我们查找每个节点ID的关联节点，然后从集合中筛选出开始和结束节点。结果如下：

+------------------------------------------------------------------------------+
| index | via                                                      | totalCost |
+------------------------------------------------------------------------------+
| 0     | ["Rotterdam", "Hoek van Holland"]                        | 265.0     |
| 1     | ["Den Haag", "Hoek van Holland"]                         | 266.0     |
| 2     | ["Rotterdam", "Den Haag", "Hoek van Holland"]            | 285.0     |
| 3     | ["Den Haag", "Rotterdam", "Hoek van Holland"]            | 298.0     |
| 4     | ["Utrecht", "Amsterdam", "Den Haag", "Hoek van Holland"] | 374.0     |
+------------------------------------------------------------------------------+

图4-7显示了Gouda和Felixstowe之间的最短路径。

图4-7.Gouda和Felixstowe之间的最短路线

图4-7中的最短路径与其他最短路径结果相比一下，会感觉很有趣。它说明，有时你可能需要考虑几个最短路径或其他选择。在这个例子中，第二条最短的路线只比最短的路线长1公里。如果我们喜欢风景，我们可以选择稍长一点的路线。

所有结对最短路径

所有结对最短路径（All Pairs Shortest Path, APSP）算法计算所有对节点之间的最短（加权）路径。相比于对图中的每一对节点运行单源最短路径算法（ Single Source Shortest Path, SSSP），APSP的效率更高。

APSP是通过跟踪迭代过程中已计算的距离并在节点上进行并行优化。在计算到未遍历节点的最短路径时，可以复用这些已知距离。你可以按照下一节中的示例，更好地了解算法的工作原理。

有些节点之间可能无法相互的连接，这意味着这些节点之间没有最短路径。算法不会返回这些节点对的距离。

APSP的原理

当你按照如下的顺序来考察时，就会很容易理解APSP。图4-8中的表将从节点A开始运行。

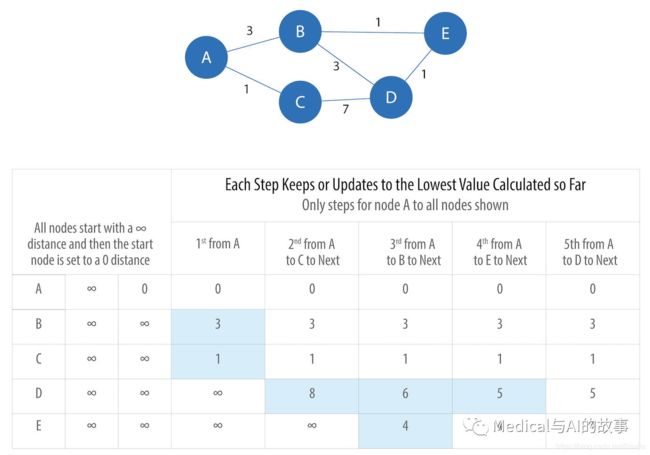
图4-8.从节点A到所有其他节点的最短路径的步骤，其中更新的数据用蓝色的底色显示
一开始，APSP算法假定到所有节点之间距离为无限远（∞）。选择开始节点后，到该节点的距离设置为0。之后的计算过程如下：

1. 从开始节点A，我们评估移动到可到达的节点的成本，并更新成本的值。在B（成本为3）或C（成本为1），我们选择最小的成本。结果是，我们选择C继续下一阶段的遍历。

2. 现在，从节点C作为中间节点，算法更新从A到所有C能直接到达节点的累积距离。当只有找到的距离成本时，才会更新值：A=0，B=3，C=1，D=8，E=∞，此时D被更新。

3. B还没有被选择成为中间节点，这次选择B作为中间节点，节点B与节点A、D和E有关系。算法通过将从A到B的距离与从B到邻近节点（A、E、E）的距离相加来计算到这些节点的距离。请注意，从开始节点A到当前节点的最低成本始终保留为当前的成本（sunk cost, 已投入的成本）。距离（用小d表示）计算结果：
   d(A,A) = d(A,B) + d(B,A) = 3 + 3 = 6
   d(A,D) = d(A,B) + d(B,D) = 3 + 3 = 6
   d(A,E) = d(A,B) + d(B,E) = 3 + 1 = 4
   在此步骤中，从节点A到B再回到A的距离，d(A,A) = d(A,B) + d(B,A) = 3 + 3 = 6，它大于已 计算的最短距离0，因此其值不会更新。
   节点D的计算值6和E的计算值4，小于先前计算的距离，因此它们被更新。

4. 接下来选择节点E为中间节点。到D节点的累积总数5低于此前计算，因此它是唯一更新的值。

5. 当最终计算中间节点D时，没有新的最小路径权重；如果没有更新任何内容，则算法终止。
   尽管APSP算法都经过了优化，可以为每个节点并行运行计算，但对单个节点出发，已经是一个非常大的图。如果只需要计算某类节点之间的路径，请考虑使用子图。

APSP算法的使用场景

当最短路由被阻塞或变得不理想时，APSP通常用于找到所有备用路由。例如，该算法用于逻辑路由规划，以确保多样性路由的最佳多路径。当需要考虑所有或大部分节点之间的所有可能路由时，请使用APSP。
示例用例包括：

• 优化城市设施的位置和货物分配。其中一个例子是确定运输网格中不同路段上预期的交通负荷。有关更多信息，请参阅R. C. Larson和A. R. Odoni的著作, Urban Operations Research (Prentice-Hall)。
• 作为数据中心设计算法的一部分，查找具有最大带宽和最小延迟的网络。在A.R.Curtis等人的论文REWIRE: An Optimization-Based Framework for Data Center Network Design中，有更多关于这种方法的细节。

Apache Spark上的APSP

Spark的shortestPaths函数用于查找从所有节点到一组称为地标的节点的最短路径。如果我们想找到从每个地点到 Colchester, Immingham, 和Hoek van Holland的最短路径，我们将编写以下查询：

result = g.shortestPaths(["Colchester", "Immingham", "Hoek van Holland"])
result.sort(["id"]).select("id", "distances").show(truncate=False)

在PySpark中运行该代码，我们将看到这个输出：

+----------------+--------------------------------------------------------+
|id              |distances                                               |
+----------------+--------------------------------------------------------+
|Amsterdam       |[Immingham -> 1, Hoek van Holland -> 2, Colchester -> 4]|
|Colchester      |[Colchester -> 0, Immingham -> 3, Hoek van Holland -> 3]|
|Den Haag        |[Hoek van Holland -> 1, Immingham -> 2, Colchester -> 4]|
|Doncaster       |[Immingham -> 1, Colchester -> 2, Hoek van Holland -> 4]|
|Felixstowe      |[Hoek van Holland -> 1, Colchester -> 2, Immingham -> 4]|
|Gouda           |[Hoek van Holland -> 2, Immingham -> 3, Colchester -> 5]|
|Hoek van Holland|[Hoek van Holland -> 0, Immingham -> 3, Colchester -> 3]|
|Immingham       |[Immingham -> 0, Colchester -> 3, Hoek van Holland -> 3]|
|Ipswich         |[Colchester -> 1, Hoek van Holland -> 2, Immingham -> 4]|
|London          |[Colchester -> 1, Immingham -> 2, Hoek van Holland -> 4]|
|Rotterdam       |[Hoek van Holland -> 1, Immingham -> 3, Colchester -> 4]|
|Utrecht         |[Immingham -> 2, Hoek van Holland -> 3, Colchester -> 5]|
+----------------+--------------------------------------------------------+

在“distance”列中每个地点旁边的数字是从源节点到该位置需要穿过的城市之间的关系（道路）数。在我们的例子中，Colchester是我们的目的地城市之一，你可以看到它有0个节点需要穿过才能到达它自己，但是从Immingham和Hoek van Holland那里要经历三个跃点。如果我们计划旅行，我们可以利用这些信息来帮助我们最大限度地利用时间。

Neo4j上的APSP

Neo4j实现了APSP的并行算法，该算法返回每对节点之间的距离。
该Procedure的第一个参数是用于计算最短权重路径的属性。如果我们将其设置为空，那么算法将计算所有节点对之间的无权重最短路径。
运行如下查询：

CALL algo.allShortestPaths.stream(null)
YIELD sourceNodeId, targetNodeId, distance
WHERE sourceNodeId < targetNodeId
RETURN algo.getNodeById(sourceNodeId).id AS source,
algo.getNodeById(targetNodeId).id AS target,
distance
ORDER BY distance DESC
LIMIT 10

此算法返回每对节点之间的最短路径两次，每次以其中的一个节点为源节点。如果你评估单向街道的有向图，这将很有帮助。但是，我们不需要看到每个路径两次，因此我们使用sourceNodeId < targetNodeId 这个谓词来筛选，保留其中一个。
结果如下：

+----------------------------------------+
| source       | target       | distance |
+----------------------------------------+
| "London"     | "Gouda"      | 5.0      |
| "Utrecht"    | "Ipswich"    | 5.0      |
| "London"     | "Rotterdam"  | 5.0      |
| "Colchester" | "Gouda"      | 5.0      |
| "Utrecht"    | "Colchester" | 5.0      |
| "Amsterdam"  | "Colchester" | 4.0      |
| "Immingham"  | "Ipswich"    | 4.0      |
| "Den Haag"   | "Colchester" | 4.0      |
| "Doncaster"  | "Felixstowe" | 4.0      |
| "Utrecht"    | "Felixstowe" | 4.0      |
+----------------------------------------+

这个输出显示了10对位置，它们之间的经历的关系最多，因为我们要求按降序排列结果（desc）。

如果要计算最短的加权路径，那就不将空值作为第一个参数传递，而是传递包含最短路径计算中使用的成本的属性名。这样，算法对该属性进行评估，得出每对节点之间的最短加权路径。
运行如下查询：

CALL algo.allShortestPaths.stream("distance")
YIELD sourceNodeId, targetNodeId, distance
WHERE sourceNodeId < targetNodeId
RETURN algo.getNodeById(sourceNodeId).id AS source,
algo.getNodeById(targetNodeId).id AS target,
distance
ORDER BY distance DESC
LIMIT 10

结果如下：

+---------------------------------------------+
| source      | target             | distance |
+---------------------------------------------+
| "Doncaster" | "Hoek van Holland" | 529.0    |
| "Doncaster" | "Rotterdam"        | 528.0    |
| "Doncaster" | "Gouda"            | 524.0    |
| "Immingham" | "Felixstowe"       | 511.0    |
| "Den Haag"  | "Doncaster"        | 502.0    |
| "Immingham" | "Ipswich"          | 489.0    |
| "Utrecht"   | "Doncaster"        | 489.0    |
| "Utrecht"   | "London"           | 460.0    |
| "Immingham" | "Colchester"       | 457.0    |
| "Immingham" | "Hoek van Holland" | 455.0    |
+---------------------------------------------+

现在我们看到的是所有最短距离节点对中最远的10个节点对。注意，Doncaster和其他荷兰的城市一起出现。如果我们想在这这些地区进行一次公路旅行的话，看起来要开很长的路。

单源最短路径

单源最短路径（Single Source Shortest Path，SSSP）算法在Dijkstra的最短路径算法的相同时间前后出现，作为单一最短路径和单源所有最短路径问题的实现。

SSSP算法计算了从根节点到图中所有其他节点的最短（权重）路径，如图4-9所示。

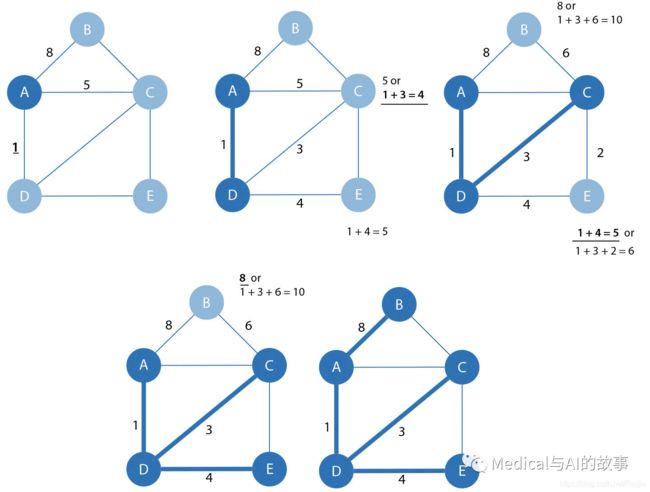
图4-9单源最短路径算法的步骤

它是按照如下的步骤工作的

1. 它始于一个根节点，与这个根节点相关所有的路径都将被测量。在图4-9中，我们选择了一个节点A作为根。
2. 从根节点计算出权重最小的附近节点，并将这个节点选择出来，加入到树中，与此一同被加入树上的还有和这个节点相连的其他节点。在这个例子中，d(A,D)=1。
3. 任何未访问节点中，从根节点到它的累积权重最小的节点被选择出来，被添加到树上。我们在图4-9中的选择是d(A,B)=8,d(A,C)=5或者是A-D-C这个路径的4，d(A,E)=5，因此，A-D-C被选中，C被添加到树上。
4. 持续按照这个进行下去，直到没有新的节点被添加进来，我们就得到了SSSP的最终结果。

SSSP算法的使用场景

当你需要评估从一个固定的起始点到所有其它单个节点的最佳路径时，就适合使用SSSP。因为路由是根据一个节点到根节点的总路径权重来选择的，所以SSSP算法被用来确定到每个节点的最佳路径，但在所有节点都需要被访问的遍历中（比如，汉密尔顿路径），这个算法是不适用的。
例如，SSSP有助于确定用于紧急服务的主要路线，因为在每次一次事故中，你并不需要到每个地点，你只需要全部计算并评估它。在垃圾回收的场景中，SSSP并不适用，因为垃圾回收的场景中，你必须要到达每个地点（在后者这个场景中，就可以使用最小生成树的算法，这将在后面讲到）。
示例用法包括

• 探测拓扑变化，如链接失败，并建议在第二个路径结构中采用新的路径结构。
• 在像局域网（LAN）这样的自主系统中，使用Dijkstra的IP路由协议场景。

Apache Spark上的SSSP

我们可以改编shortest_path函数来计算一个节点到所有其他节点的距离。注意，我们将再次使用Spark的aggregateMessages框架来定制我们的函数。
我们将首先导入与以前相同的库：

from graphframes.lib import AggregateMessages as AM
from pyspark.sql import functions as F

我们使用相同的用户定义函数来构造路径：

add_path_udf = F.udf(lambda path, id: path + [id], ArrayType(StringType()))

以下是主函数，它计算从源节点开始的最短路径：

def sssp(g, origin, column_name="cost"):
    vertices = g.vertices.withColumn("visited", F.lit(False)).withColumn("distance",F.when(g.vertices["id"] == origin, 0).otherwise(float("inf"))).withColumn("path", F.array())
    cached_vertices = AM.getCachedDataFrame(vertices)
    g2 = GraphFrame(cached_vertices, g.edges)
    
    while g2.vertices.filter('visited == False').first():
        current_node_id = g2.vertices.filter('visited == False').sort("distance").first().id
        msg_distance = AM.edge[column_name] + AM.src['distance']
        msg_path = add_path_udf(AM.src["path"], AM.src["id"])
        msg_for_dst = F.when(AM.src['id'] == current_node_id, F.struct(msg_distance, msg_path))
        new_distances = g2.aggregateMessages(F.min(AM.msg).alias("aggMess"), sendToDst=msg_for_dst)
        new_visited_col = F.when(g2.vertices.visited | (g2.vertices.id == current_node_id), True).otherwise(False)
        new_distance_col = F.when(new_distances["aggMess"].isNotNull() &
                                  (new_distances.aggMess["col1"] < g2.vertices.distance),
                                  new_distances.aggMess["col1"]) \
                            .otherwise(g2.vertices.distance)
        new_path_col = F.when(new_distances["aggMess"].isNotNull() &
                              (new_distances.aggMess["col1"] < g2.vertices.distance),
                              new_distances.aggMess["col2"].cast("array")) \
                        .otherwise(g2.vertices.path)
        new_vertices = g2.vertices.join(new_distances, on="id", how="left_outer") \
            .drop(new_distances["id"]) \
            .withColumn("visited", new_visited_col) \
            .withColumn("newDistance", new_distance_col) \
            .withColumn("newPath", new_path_col) \
            .drop("aggMess", "distance", "path") \
            .withColumnRenamed('newDistance', 'distance') \
            .withColumnRenamed('newPath', 'path')
        cached_new_vertices = AM.getCachedDataFrame(new_vertices)
        g2 = GraphFrame(cached_new_vertices, g2.edges)
    return g2.vertices \
                .withColumn("newPath", add_path_udf("path", "id")) \
                .drop("visited", "path") \
                .withColumnRenamed("newPath", "path")

如果我们想找到从Amsterdam到所有其他地点的最短路径，我们可以这样调用函数：

via_udf = F.udf(lambda path: path[1:-1], ArrayType(StringType()))
result = sssp(g, "Amsterdam", "cost")
(result
.withColumn("via", via_udf("path"))
.select("id", "distance", "via")
.sort("distance")
.show(truncate=False))

我们定义了这个函数，从结果路径中过滤出开始和结束节点。如果运行该代码，结果如下：

+----------------+--------+-------------------------------------------------------------+
|id              |distance|via                                                          |
+----------------+--------+-------------------------------------------------------------+
|Amsterdam       |0.0     |[]                                                           |
|Utrecht         |46.0    |[]                                                           |
|Den Haag        |59.0    |[]                                                           |
|Gouda           |81.0    |[Utrecht]                                                    |
|Rotterdam       |85.0    |[Den Haag]                                                   |
|Hoek van Holland|86.0    |[Den Haag]                                                   |
|Felixstowe      |293.0   |[Den Haag, Hoek van Holland]                                 |
|Ipswich         |315.0   |[Den Haag, Hoek van Holland, Felixstowe]                     |
|Colchester      |347.0   |[Den Haag, Hoek van Holland, Felixstowe, Ipswich]            |
|Immingham       |369.0   |[]                                                           |
|Doncaster       |443.0   |[Immingham]                                                  |
|London          |453.0   |[Den Haag, Hoek van Holland, Felixstowe, Ipswich, Colchester]|
+----------------+--------+-------------------------------------------------------------+

在这些结果中，我们可以看到从Amsterdam这个根根节点到图中所有其他城市的物理距离（以公里为单位），由短到长排序。

Neo4j上SSSP

Neo4j实现了SSSP的变体，被称之为增量步进算法（Delta-Stepping Algorithm），它将Dijkstra的算法分为多个可以并行执行的阶段。
执行以下的查询：

MATCH (n:Place {id:"London"})
CALL algo.shortestPath.deltaStepping.stream(n, "distance", 1.0)
YIELD nodeId, distance
WHERE algo.isFinite(distance)
RETURN algo.getNodeById(nodeId).id AS destination, distance
ORDER BY distance

结果如下：

+-------------------------------+
| destination        | distance |
+-------------------------------+
| "London"           | 0.0      |
| "Colchester"       | 106.0    |
| "Ipswich"          | 138.0    |
| "Felixstowe"       | 160.0    |
| "Doncaster"        | 277.0    |
| "Immingham"        | 351.0    |
| "Hoek van Holland" | 367.0    |
| "Den Haag"         | 394.0    |
| "Rotterdam"        | 400.0    |
| "Gouda"            | 425.0    |
| "Amsterdam"        | 453.0    |
| "Utrecht"          | 460.0    |
+-------------------------------+

在这些结果中，我们可以看到图中从根节点London到所有其他城市的物理距离（以公里为单位），由短到长排序。

最小生成树

最小（加权）生成树算法（Minimum Spanning Tree, MST）是从一个给定的节点开始，到其所有可到达的节点并使得经过这些节点的权重尽可能地小。它从已被访问的节点出发，根据最小权重访问下一个节点，而且不产生环。
捷克科学家Otakar Borůvka于1926年开发了第一个已知的最小（权重）生成树算法。Prim的算法，发明于1957年，是最简单和最著名的。Prim的算法类似于Dijkstra的最短路径算法，但它不是最小化每个关系的路径总长度，而是单独优化每个关系的长度。与Dijkstra的算法不同，它允许权重为负。
最小生成树算法的操作如图4-10所示。

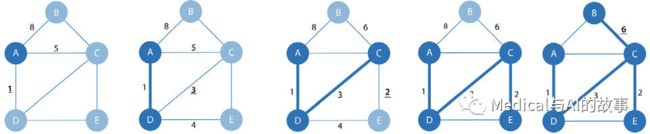
图4-10.最小生成树算法的步骤

步骤如下：

• 起初，树只包含一个节点。在图4-10中，我们从节点A开始。
• 将选择来自该节点的最小权重的关系并将其添加到树（及其连接的节点）。在当前的案例中，是A-D。
• 这个过程是重复的，总是选择连接树中任何节点的最小权重关系。
  如果将这里的示例与图4-9中的SSSP示例进行比较，你会注意到在第四个图中，路径会有所不同。这是因为SSSP根据从根开始的累计总数来计算最短路径，而最小生成树只考虑下一步的成本。
• 当没有更多要添加的节点时，树是最小生成树。这种算法还有一些变体，可以找到最大权重生成树（最高成本树）和K生成树（树大小有限）。

MST算法的使用场景

当需要访问所有节点的最佳路由时，请使用最小生成树。因为路由是根据下一步的成本来选择的，所以当你必须在一次行走中访问所有节点时，它非常有用。
你可以使用此算法优化连接系统（如水管和电路设计）的路径。它还用于近似一些计算时间未知的问题，如商旅问题和某些类型的路线问题。虽然该算法不一定总能找到绝对最优解，但它使得实际上相当复杂和密集的计算更加容易接近。
示例用例包括：

• 尽可能降低探索一个国家的旅行成本。“An Application of Minimum Spanning Trees to Travel Planning”描述了算法如何分析航空和海上航线来实现这一点。
• 使得货币回报之间的相关性。这在“Minimum Spanning Tree Application in the Currency Market”中进行了描述。
• 追踪疫情中感染传播的历史。有关更多信息，请参阅““Use of the Minimum Spanning Tree Model for Molecular Epidemiological Investigation of a Nosocomial Outbreak of Hepatitis C Virus Infection”。

最小生成树算法只在关系具有不同权重的图上运行时给出有意义的结果。如果图没有权重，或者所有关系都有相同的权重，那么任何生成树都是最小生成树。

Neo4j上的最小生成树

让我们看看MST算法的作用。以下查询查找从Amsterdam开始的生成树：

MATCH (n:Place {id:"Amsterdam"})
CALL algo.spanningTree.minimum("Place", "EROAD", "distance", id(n), {write:true, writeProperty:”mst"})
YIELD loadMillis, computeMillis, writeMillis, effectiveNodeCount
RETURN loadMillis, computeMillis, writeMillis, effectiveNodeCount

传递给此算法的参数为：

此查询将其结果存储在图中。如果要返回最小权重生成树，再运行如下查询：

MATCH path = (n:Place {id:"Amsterdam"})-[:MINST*]-()
WITH relationships(path) AS rels
UNWIND rels AS rel
WITH DISTINCT rel AS rel
RETURN startNode(rel).id AS source, endNode(rel).id AS destination,
rel.distance AS cost

结果如下：（译者：Neo4j 3.5.7+Algo3.5.4.0上的MST算法可能有问题）

+-------------------+--------------------+----------+
| source            | destination        | cost     |
+-------------------+--------------------+----------+
| "Amsterdam"       | "Utrecht"          | 46.0     |
| "Utrecht"         | "Gouda"            | 35.0     |
| "Gouda"           | "vRotterdam"       | 25.0     |
| "Rotterdam"       | "Den Haag"         | 26.0     |
| "Den Haag"        | "Hoek van Holland" | 27.0     |
| "Hoek van Holland"| "Felixstowe"       | 207.0    |
| "Felixstowe"      | "Ipswich"          | 22.0     |
| "Ipswich"         | "Colchester"       | 32.0     |
| "Colchester"      | "London            | 106.0    |
| "London"          | "Doncaster"        | 277.0    |
| "Doncaster"       | "Immingham"        | 74.0     |
+-------------------+--------------------+----------+

图4-11.Amsterdam的最小权重生成树

如果我们在Amsterdam，并且想在同一次旅行中访问示例数据集当中的其他地方，图4-11显示了最短的连续路线。

随机行走

随机行走算法(Random Walk，RW)会在图中的随机路径上给我们提供一组节点。Karl Pearson在1905年给《Nature》杂志的一封题为“The Problem of the Random Walk”的信中首次提到了这个词。尽管这一概念可以追溯到更远的地方，但直到最近，随机行走才被应用到网络科学中。

一般来说，一次随机行走有时被描述为类似于醉汉如何穿越城市。他们知道他们想要到达的方向或终点，但可能会走一条非常迂回的路线到达那里。
该算法从一个节点开始，在某种程度上随机地跟踪一个关系向前或向后到邻居节点。然后，它从该节点执行相同的操作，依此类推，直到达到设置的路径长度。（我们说有点随机，因为一个节点和它的邻居之间的关系数量会影响一个节点被遍历的概率。）

RW的使用场景

当需要生成一组大部分随机连接的节点时，可以将随机行走算法用作其他算法或数据管道的一部分。
示例用例包括：

• 作为node2vec和graph2vec算法的一部分，创建节点嵌入。这些节点嵌入可以用作神经网络的输入。
• 作为Walktrap和Infomap社区检测的一部分。如果随机行走重复返回一小组节点，则表明节点集可能具有社区结构。
• 作为机器学习模型训练过程的一部分。这一点在David Mack的文章Review Prediction with Neo4j and TensorFlow中有进一步的描述。
  你可以在N. Masuda, M. A. Porter, 和 R. Lambiotte的一篇论文中阅读更多的用例，Random Walks and Diffusion on Networks。

Neo4j上的RW算法

Neo4j实现了随机游走算法。它支持在算法的每个阶段选择下一个要遵循的关系的两种模式：

• random，随机选择要跟踪的关系
• node2vec，根据计算前一个邻居的概率分布选择要跟踪的关系
  执行以下查询：

MATCH (source:Place {id: "London"})
CALL algo.randomWalk.stream(id(source), 5, 1)
YIELD nodeIds
UNWIND algo.getNodesById(nodeIds) AS place
RETURN place.id AS place

传递给此算法的参数为：

返回结果如下：

+--------------+
| place        |
+--------------+
| "London"     |
| "Colchester" |
| "Ipswich"    |
| "Felixstowe" |
| "Ipswich"    |
| "Felixstowe" |
+--------------+

在随机行走的每个阶段，算法随机选择下一个关系。这意味着，如果我们重新运行算法，即使使用相同的参数，我们可能也不会得到相同的结果。步行也有可能自行返回，如图4-12所示，从Amsterdam到Den Hagg再返回。

图4-12.从London开始的随机行走

总结

路径查找算法（Pathfinding algorithms）对于理解数据的连接方式很有用。在本章中，我们首先介绍了基本的广度和深度优先算法（BFS & DFS），然后再介绍Dijkstra和其他最短路径算法（Shortest Path）。我们还研究了最短路径算法的变体（A* & Yen’s），这些算法优化后可以找到从一个节点到所有其他节点（SSSP）或图中所有节点对之间的最短路径（APSP）。我们完成了随机游走算法（Random Walk），可以用来寻找任意路径集。
接下来我们将学习中心性算法，它可以用来在图中找到有影响的节点。

算法资源
有许多算法书籍，但有一本是最突出的，它涵盖了基本概念和图算法：《Algorithm Design Manual》，由Steven S.Skiena（Springer）撰写。我们强烈推荐这本教科书给那些寻求关于经典算法和设计技术的综合资源的人，或者那些只想深入了解各种算法如何操作的人。