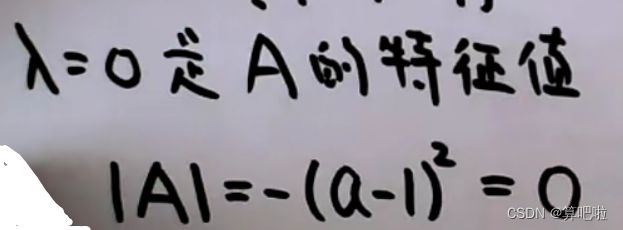算吧啦

线性代数知识

❀关于李永乐-线性代数基础班学习笔记。

第一章行列式

1.1 行列式的概念

1.1.1 二、三阶行列式

若有二元一次方程组，进行加减消元：

根据相加相减的系数，可以提炼成二阶行列式

假设方程组系数行列式不为0，则可让分母做运算。

若解三元一次方程组，很自然会出现3个数加加减减。

注意只有二三阶才可以直接根据主副对角线判定前面的正负。

1.1.2 排列、逆序、逆序数

第二个例子：对于2，针对1有逆序；对于4，针对3、1有逆序；对于3，针对1有逆序。

第四个例子：自然排列逆序数是0

1.1.3 n阶行列式概念

用【逆序数】来判断前面的正负。

【上三角行列式】
>

（要想行列式不为0，便只有这一种可能性）

【副对角线行列式】

注意是四阶，不可以直接根据副对角线，就判断前面是负号。

【法一】

【法二】

1.2 行列式的性质

【法一】倍加性质

c2-c1；c3-c1

c1+c2+c3

c2、c3分别提取公因数-1

【法二】用性质5，和的拆开

第一、第二、第三列均可拆成2个，则一共可以拆成8个行列式；

在这8个行列式中，存在两列是相同的情况，则行列式值为0；

则把不为0的写出来：

用两行互换的性质（换两次正负号不变）

1.3 行列式按行(列)展开公式

1.3.1 余子式、代数余子式

去掉一行及一列，剩下的元素就是余子式

带正负号的这样一个n-1阶行列式就是aij的代数余子式

1.3.2 展开公式

引入：

证明：

注意A31与a31的数值大小无关…类似A32、A33。

因此构造的新的行列式B，第三行用系数表示

按照第三行展开。又这个行列式两行相同，因此行列式值=0

1.3.3 重要公式

(3) 对角线有一块为0。mn是行列式AB的阶数。

法2：

r2、r3、r4均加上 -a倍的r1

**【分析2】**不看主对角线，每一列都一样。就是隐形的爪形
变成爪形后，把每一列都加到第一列

**【分析三】**把上一行的-1倍加到下一行（由第三行开始，即第三行-1倍加到第四行）
再把每一列都加到第一列


**【分析四】**给a加上0，构成两个数相加。然后可以拆成16个行列式。在这些行列式中，存在大多数两列相同的情况（即行列式值为0）

【法一】 r1加上-1 r2；r4加上-1 r3

c2-c1；c3-c4

按第一行展开
**【法二】**变成爪形：r2、r3、r4分别加上-1 r1

逐行相加：先把第一行降价到第二行

把第二行加到第三行

第三行加到第四行

【法一】

【法二】

c3+（-2 c1）

1.4 克拉默法则

n个方程n个未知数的方程组：

求x几（几为下标），就把第几列换成常数项。

【克拉默法则更可能用在小的证明题上】

第二章矩阵

【基础，应防混淆】

2.1 概念、运算

❗注意乘法的复习！
❗注意以下符号的含义

2.1.1 概念

行阶梯矩阵（不唯一）

第一行不是行阶梯矩阵：零行不在矩阵的底部

第二行不是行阶梯矩阵：第三行的7是主元，但其下面的元素不是0

第三行是行阶梯矩阵

行最简矩阵（唯一）

1、2不是行最简矩阵

3、4是行最简矩阵

解：

2.1.2 运算

（1）加法

（2）数乘

（3）乘法

性质

（4）转置

关于转置的矩阵/数的重组

【由以下可得：第一排是矩阵，第二排是数】

列在前面，行在后面得到的是一个矩阵

这样得到的行列式，两行成比例，即行列式值为0。则这种矩阵是秩为1的关系。

以下得到的两个矩阵互为转置的关系



行在前面，列在后面得到的是一个数

下面两数相等，就是矩阵的迹【矩阵的迹就是主对角线元素的和】

这个矩阵是个对称矩阵

❀例题

（2）两行成比例，是秩为1的矩阵

2.2 ❀伴随矩阵、❀可逆矩阵

❗

单位矩阵恒等变形的技巧

2.2.1 伴随矩阵

证明：

a11A11+a12A12是行列式A按照第一行展开，即行列式的值

【某一行的所有元素与另一行相应元素的代数余子式乘积之和等于0】。即 a11A21+a12A22=0

二阶矩阵的伴随

❀例题

2.2.2 可逆矩阵

注意单位矩阵恒等变形的技巧

（1）逆矩阵性质

❀例题

2.3 初等变换、❀初等矩阵

❗

【初等矩阵都有两种理解方法（如右列）】

【左乘是行变换，右乘是列变换】

【初等矩阵在第一个，第二个到第三个做的变化，就是初等矩阵在单位矩阵上做的变化】

【初等矩阵在第二个，初等矩阵由单位矩阵作出的变化就是第一个加上这个变化，得出第三个的结果】

【初等矩阵逆矩阵的三个公式】：

【倍加矩阵的逆矩阵是把倍数改成相反数】

【两行互换，初等矩阵纹丝不动，就是它自己】

【对角矩阵的逆矩阵是取倒数】

❀例题

【有下标的题目得观察下标】

但是p2是将第一行加到第三行

【将文字变为符号】

2.4 分块矩阵

❗

对应的题型
第一种：
第二种：方程组解
第三种：向量；秩（既可按行分块，也可按列分块）

【AC按列分块】

【BC按行分块】

【BC按列分块】

【通过解方程组得出B】

（1）运算

❀例题

【做乘法：分四块】

【求逆：分四块】

把B矩阵按列分块

2.5 方阵A的行列式

❀例题

第三章向量*

3.1 概念

【加法与数乘的运算法则】

3.2 线性表示

❀例题

【可用爪形消元】

3.3 相关、无关

有零向量、有成比例的向量，这样的向量组肯定是线性相关的。

对于任何一个向量组这个式子永远成立：

相关、无关的区别：有且仅有以上式子能使结果为0的才是线性无关。

❀例题

3.4 秩（向量组、矩阵）

3.4.1 向量组的秩

一个向量组的极大线性无关组多数情况下答案不唯一。【极大线性无关组中的向量个数是相同的】

向量组中的任何一个向量都可以由极大线性无关组线性表出

3.4.2 矩阵的秩

3.3.4 秩的性质

❀例题

【化为行最简】

则秩=3
极大线性无关组：找主元

法一：

法二：

法三：

【法二】

3.5 正交矩阵

第四章方程组

4.1 齐次方程组

齐次方程组不存在无解的情况。【最少都有零解】

由定理可知有两个解向量。

化成行最简后【自由向量是a3、a5.因此得到红笔书写的】。然后n1的黑笔三个数是a3列的相反数，n2的是a5列的相反数

【法二】

4.2 非齐次方程组

4.3 解的性质

❀例题

方程组通解：

【法二】

4.4 方程组的应用

4.4.1 通过解方程组得到所需矩阵

解题思路：

可以得到齐次方程组

分析：解方程组，求出方程组的解。拼成所需矩阵X。（注意把握矩阵X的行列尺寸）

解这两个方程组
【两个方程组系数项相同，考虑将两个增广矩阵拼接在一起】然后化成行最简

第五章特征值

5.1 特征值、特征向量

一个特征值的特征向量有无数多个。

（1）特征值的和就是A矩阵主对角线元素的和（即迹）
（2）特征值的乘积就是行列式的值

【求特征值、特征向量方法：】

❀例题

则可求得特征值

【上面两道题都是有重根的情况】可以发现此时有的矩阵有两个无关的特征向量，有的只有1个。这有重根的情况与后面一个矩阵是否与对角矩阵相似有关联。

…

【满足题设关系的A矩阵有无数多个，即A矩阵是不唯一的。因此此处只能求得特征值的取值范围（即有多少个1不知道，多少个-3也不知道）。因此用“或”】
举例A可能为如下：

5.2 相似矩阵

【重点：和对角矩阵相似】

5.2.1 相似的定义

例子

【由以上例题可知，一个矩阵的相似矩阵是不唯一的】

5.2.2 相似的性质

【相似具有传递性：】

【可用于证明题：证两者相似时可以找个中介】

【还有一种考法：求可逆矩阵p】

证明：

利用：如果A是可逆矩阵，则AB的秩等于B的秩证明

证明：

利用前面的定理：特征值的和是A的迹。而A、B的特征值相同，则其迹相同。

证明：

❀例题

5.2.3 相似对角化

不是每一个矩阵都能相似对角化。

证明：
【充分性】

（把A矩阵暂时看作三阶矩阵），把P矩阵按列分块（对角矩阵也是假设的）

【必要性】

（1）可逆矩阵相似对角化解题步骤

❀例题

【❗】

（注意此时由2重特征值）

n-秩=2，则秩=1。

分析：特征值一定有重根

分析：B是对角矩阵，又AB相似，则P矩阵即A的特征向量。（根据相似对角化的解题步骤）
（1）问
【法一】
需用相似的必要条件34构造一元二次方程组【4是最好用的】

【法二】

则-x=1-y -1=-y。对应可解
（2）问
分析：求A的3个特征向量

5.3 实对称矩阵

【证明】
证明正交即内积为0（红框）

由1式转置：

由A是实对称的，即A的转置就是A；再由2式：

（1）正交矩阵相似对角化解题步骤

【分为如下情况】

特征值不同，根据定理，此时已经正交。

即检查两向量是否垂直（垂直即表示已正交）
判定垂直：两向量的内积为0

如不垂直，即不正交

❀例题

【❗ 】

去掉或：运用定理1【实对称矩阵一定和对角矩阵相似】

保证对角矩阵减去单位矩阵秩为2（即减后里面只有1个0）：
（0和1的位置可以变化的）

又由于对角矩阵其各项就是特征值，则：

分析：根据秩的背景处理参数a

分析：通过研究A和那个对角矩阵相似。并以此当中间变量求取最后结果。

*第六章二次型

6.1 概念、定理

6.1.1 二次型

二次型：一个多元函数的每一项都是2次的。

中间矩阵是对称矩阵；（其主对角线是平方项系数；混合项系数：x1x2的系数倍2除摆在a12和a21的位置，x2x3的系数倍2除摆在a23a32的位置，x1x3的系数为0则摆在a13a31的位置）

【可写成3个矩阵的原因】原理：

右边的矩阵也类似与矩阵乘法的相加，因此拆分开

又A是对称矩阵

【二次型和实对称矩阵是一一对应的关系】

6.1.2 标准形

标准形：只有平方项，没有混合项

【对角矩阵和标准型一一对应】

6.1.3 规范形

规范形：必须是标准形，且平方项系数只能是+1、-1、0

6.1.4 正惯性指数、负惯性指数

正惯性指数：标准形中正平方项的个数；
负惯性指数：标准形中负平方项的个数。

【可用配方法、特征值来求得正负惯性指数】

6.1.5 二次型的秩

6.1.6 坐标变换

坐标变换的3种表现形式：

【坐标变换有无数多组】
【需要抓住重点：|C|=0、C可逆】

其中C是坐标变换中的可逆矩阵

B的转置=B意味着B是对称矩阵，即为新的二次型表示，B记为新的二次型矩阵

6.1.7 合同

这两矩阵肯定不相似（迹不同）

【合同的性质】

证明：

（判断两个矩阵是否合同）：（即抓住正负惯性指数）

证明-利用定理：二次型经过坐标变换，其正负惯性指数不会变。

（1）是最好的方法
接下来介绍其他方法
（2）
如果假设合同，两边算行列式

C可逆，|C|不为0。|C|平方>0，则|A|、|B|正负号相同

6.2 化成标准形

证明：
（把Q矩阵当作坐标变换里的C矩阵）
正交矩阵，其逆等于其转置矩阵

（对角矩阵的各项就是标准形平方项的系数，又对角矩阵就是A的特征值）->因此标准形以特征值作为平方项的系数：

❀例题

分析：给了标准形相当于给了特征值。注意三个自变量，因此特征值应该是1、4、0。

看到二次型，可写出矩阵A

0是A的特征值，意味着行列式A的值=0

P是特征向量，第一列是1的特征向量，第二列是4的特征向量，第三列是0的特征向量（对应特征值的特征向量）

注意正交矩阵的几何意义：列向量一定是两两垂直的，列向量是单位向量。因此要单位化

注意特征值都不同，因此对应的特征向量已相互正交

分析：先处理x1

处理中括号-让中括弧完全平方

中括号是完全平方了，然后打开后面的平方项，进行合并同类项

开始处理x2（同x1），整理x3

（上三角）

分析：对于没有平方项的，可以先做一次准备工作–做一次坐标变换构造出平方项。【一般习惯用a+b、a-b的形式】。为了保证坐标变换行列式不等于0，因此令x3=y3

然后带入原式，构造出平方项

开始配方


注意：经过了两次坐标变换。

把以下标准形变成规范形