散度、旋度的推导

散度

---

假设我们可以用 $F$ 来表示一滩液体的流动情况，那么我们该如何判断这摊液体有没有一处像喷泉一样不断流出液体的点（源点）或一处像地漏一样不断流入液体的点（汇点）呢？

这就需要引入 散度 的概念。

假设空间中有向量场 $F=F_{x}i+F_{y}j+F_{z}z$，我们想知道点 $P(x,y,z)$ 是不是源 / 汇点，最直观的想法就是判断流入的量和流出的量，若相等，则不是源 / 汇点，若流入大于流出，则是汇点，反之就是源点。

现在的问题就是，如何计算流入和流出的多少呢？

假设点 $P$ 在一个长方体内部，长方体边长为 $(\Delta x,\Delta y,\Delta z)$

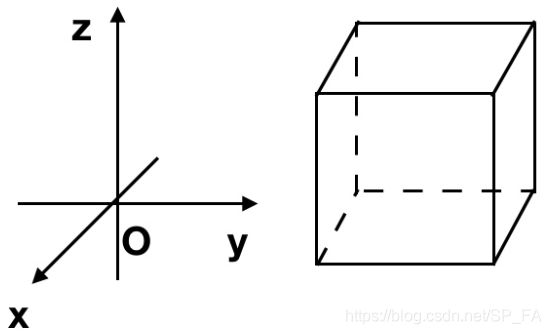
此时我们可以计算每个面的流量（或者叫通量），以 $x$ 轴正方向为正面，负方向为背面，计算两个面的通量差，再分别计算沿 $y,z$ 轴方向的通量差，最后 $x,y,z$ 方向通量差之和就可以用来比较流入和流出量的多少了。

以 $x$ 方向为例，正、背面的流量如下：$$\begin{array}{rl}\underset{front}{\iint }{F}_x(x,y,z)\mathrm{d}S& \simeq F_x(x+\frac{\Delta x}{2},y,z)\Delta y\Delta z\\ \underset{back}{\iint }{F}_x(x,y,z)\mathrm{d}S& \simeq -F_x(x-\frac{\Delta x}{2},y,z)\Delta y\Delta z\end{array}$$

流量差：$$\begin{array}{rl}\underset{front+back}{\iint }{F}_x(x,y,z)\mathrm{d}S& =F_x(x+\frac{\Delta x}{2},y,z)\Delta y\Delta z-F_x(x-\frac{\Delta x}{2},y,z)\Delta y\Delta z\\ & =\frac{F_x(x+\frac{\Delta x}{2},y,z)-F_x(x-\frac{\Delta x}{2},y,z)}{\Delta x}\Delta x\Delta y\Delta z\end{array}$$

我们最终是判断 $P$ 点的流量差，可以看作是当长方体非常非常小时的通量密度，也就是流量差除以体积：$$\begin{array}{rl}\Delta V& =\Delta x\Delta y\Delta z\\ \underset{\Delta V\to 0}{\lim }\frac{1}{\Delta V}\underset{front+back}{\iint }{F}_x(x,y,z)\mathrm{d}S& =\underset{\Delta x\to 0}{\lim }\frac{F_x(x+\frac{\Delta x}{2},y,z)-F_x(x-\frac{\Delta x}{2},y,z)}{\Delta x}\\ & =\frac{\partial F_x}{\partial x}\end{array}$$

三个方向相加，最后得出：$$\mathrm{d}\mathrm{i}\mathrm{v}F=\frac{\partial F_x}{\partial x}+\frac{\partial F_y}{\partial y}+\frac{\partial F_z}{\partial z}=\nabla \cdot F$$好。

旋度

---

还是那一滩液体，现在我们想确定每一个点的旋转情况（逆时针还是顺时针）此时就需要用到旋度。

假设向量场 $F=F_{x}i+F_{y}j$，点 $P(x,y)$ 在一个矩形内部，矩形边长为 $\Delta x,\Delta y$

我们分别计算四个边对于旋转的贡献，以 $C_T,C_B$ 边为例，假设 $C_T$ 边的通量 $\varphi (C_T)$ 是顺时针方向（不要看上图的方向）$C_B$ 边的通量$\varphi (C_B)$是逆时针方向，若 $\varphi (C_T)<\varphi (C_B)$，则该点在沿 $y$ 轴方向更倾向于逆时针旋转，最后把沿每个轴的倾向加和，就是该点的旋转方向。

求通量：$$\begin{array}{rl}\underset{C_B}{\int }{F}_x\mathrm{d}x& \simeq F_x(x,y-\frac{\Delta y}{2})\Delta x\\ \underset{C_T}{\int }{F}_x\mathrm{d}x& \simeq -F_x(x,y+\frac{\Delta y}{2})\Delta x\\ \underset{C_B+C_T}{\int }{F}_x\mathrm{d}x& =-\frac{F_x(x,y+\frac{\Delta y}{2})-F_x(x,y-\frac{\Delta y}{2})}{\Delta y}\Delta x\Delta y\end{array}$$

然后除以面积，因为我们算每条边对该点旋转方向的贡献，在矩形非常非常小时，可以近似看成通量在该矩形表面的密度。$$\begin{array}{rl}\underset{\Delta S\to 0}{\lim }\frac{1}{\Delta S}\underset{C_B+C_T}{\int }{F}_x\mathrm{d}x& =-\frac{F_x(x,y+\frac{\Delta y}{2})-F_x(x,y-\frac{\Delta y}{2})}{\Delta y}\\ & =-\frac{\partial F_x}{\partial y}\end{array}$$

再算出 $C_L+C_R$ 并求和 ：$$C=(\frac{\partial F_y}{\partial x}-\frac{\partial F_x}{\partial y})k=\nabla \times F$$

$C$ 即是旋度，是一个向量，利用右手螺旋定则即可判断该点的旋转方向。

当然，这只是 $xy$ 平面的，在三维空间中，我们还有另外两个平面：$$\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{l}F=(\frac{\partial F_z}{\partial y}-\frac{\partial F_y}{\partial z})i+(\frac{\partial F_x}{\partial z}-\frac{\partial F_z}{\partial x})j+(\frac{\partial F_y}{\partial x}-\frac{\partial F_x}{\partial y})k$$

旋度的物理意义

维基百科上的一张图：

飞机起飞时喷射出的气体的旋度即是飞机飞行方向，而气流旋转方向就可以用右手螺旋定则判断。