数学建模———层次分析法及其matlab语法，函数和代码实现
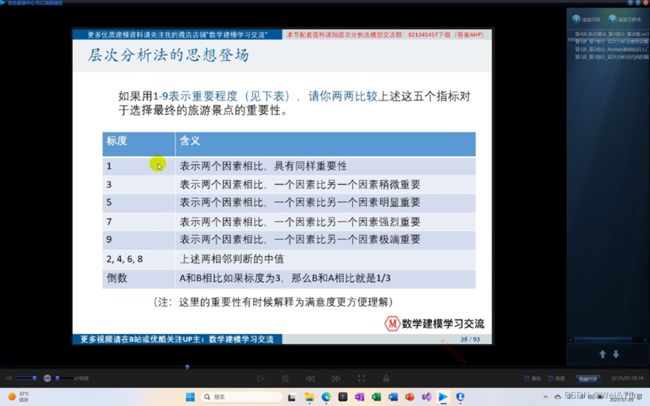
- 层次分析法思想登场
建模比赛中最基础的模型之一，其主要用于解决评价类问题（例如：选择那种方案最好，哪位运动员或者员工表现的更优秀。）
评价类问题字眼：
- 评价的目标是什么？
- 达到这个目标有那几种方案？
- 评价准则或指标是什么？
确定权重的方方法——分而治之
（两两比较推算出权重）
比较的标度：
例子引用（本文引用的例子及博主跟的课中举的例子）
旅游景点的选择
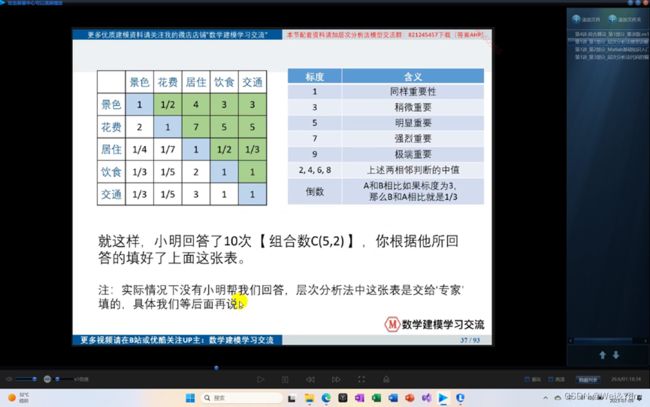
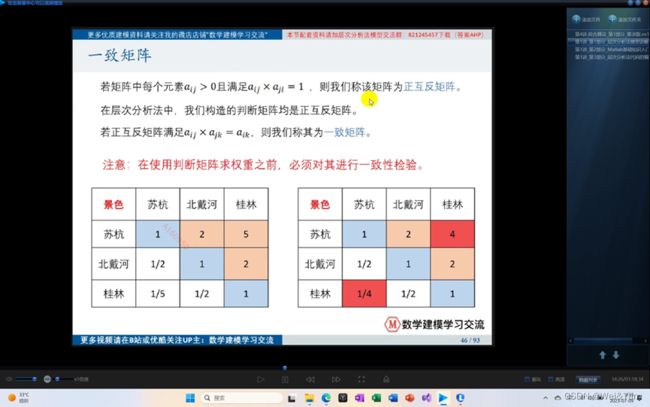
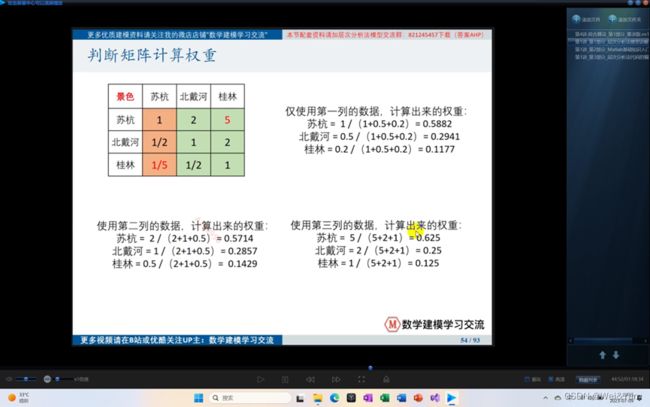
正互反矩阵/判断矩阵：
根据标度所填的矩阵有着一定的规律矩阵中坐标[I,j]与坐标[j,i]的两个元素相乘为1且坐标i==j的元素为1.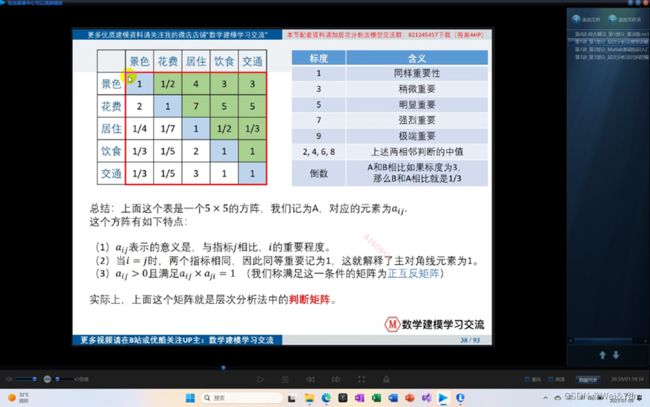
一个不成问题的问题：
在填入矩阵的时候我们填入的数值可能会出现矛盾，此时需要做出修改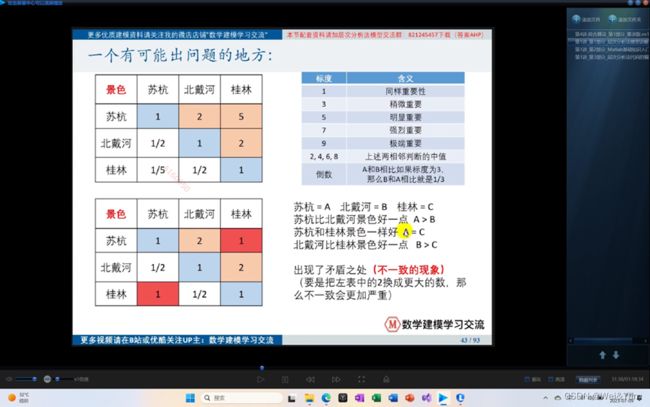
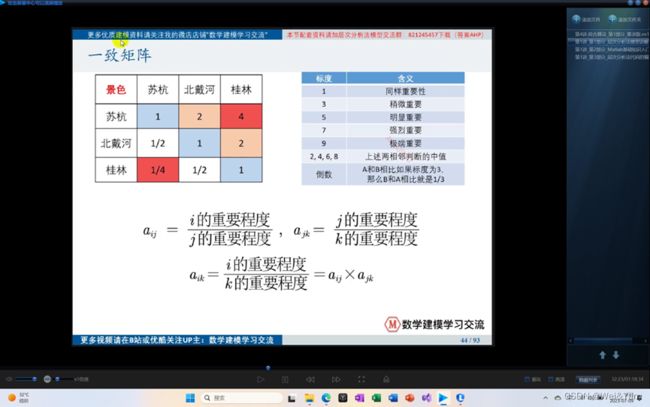
一致矩阵：
特点：各行/各列成倍数关系且一定是正互反矩阵
一致性矩阵的定义：
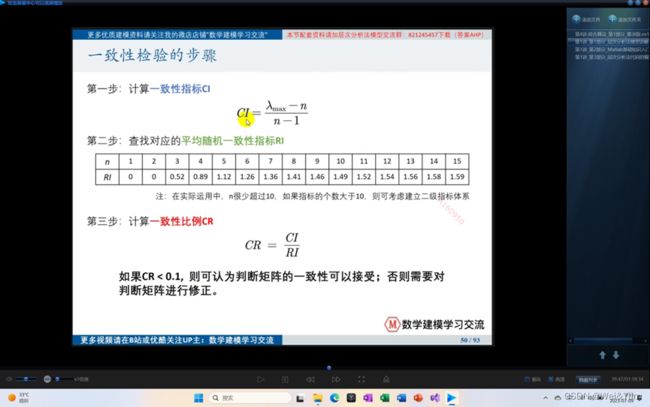
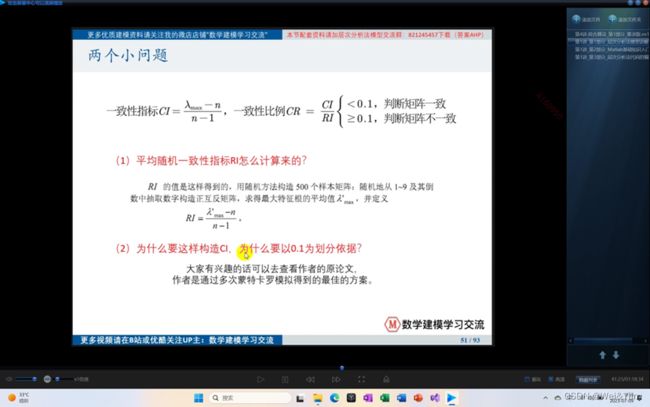
一致性矩阵的检验：
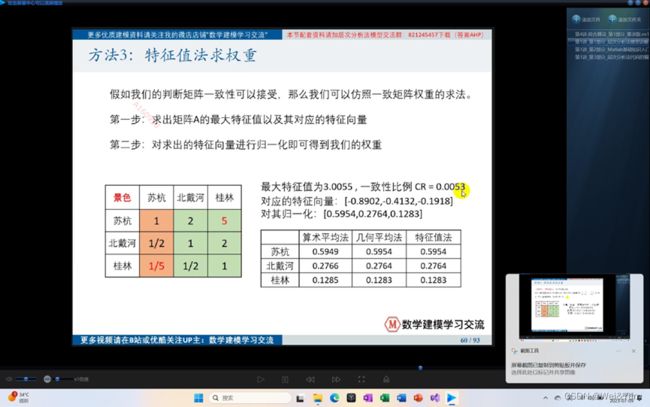
计算CI中λmax 是最大特征值（后面将特征值求权重时会解释），n是方形矩阵的行/列（因为为方形矩阵所以行=列）
RI是课中给出的
计算权重：
（由于计算权重方法的原理文字或口头叙述过于枯燥，晦涩，我们直接告诉方法，后面在代码实现的时候我们会详细讲解。）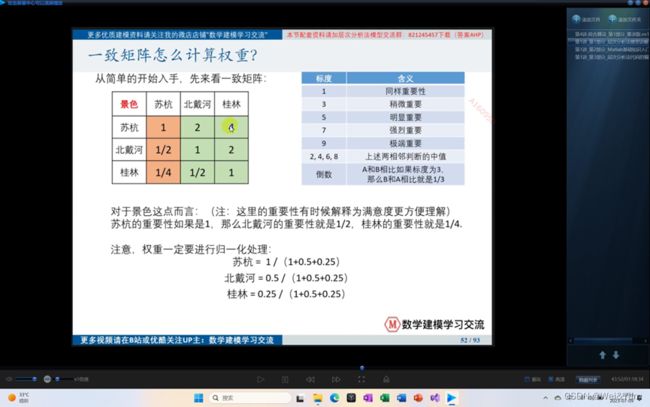
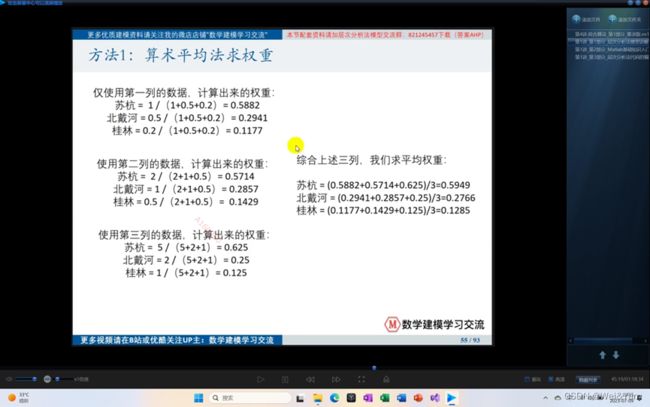
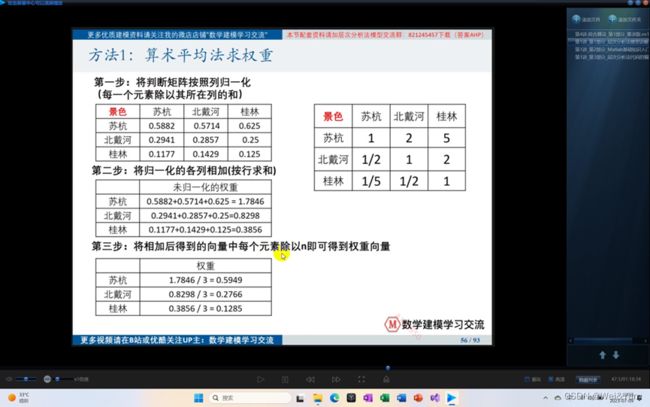
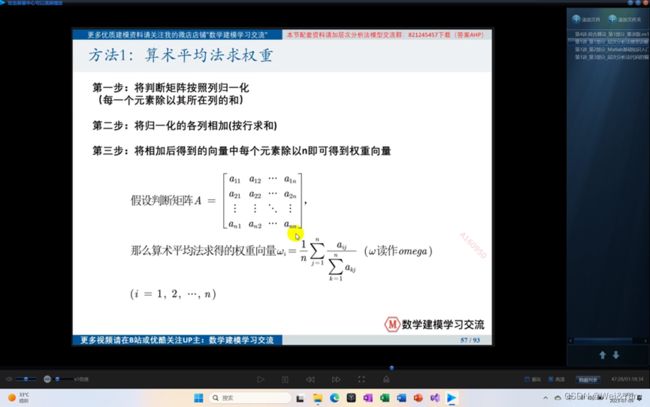
- 算数平均法求权重
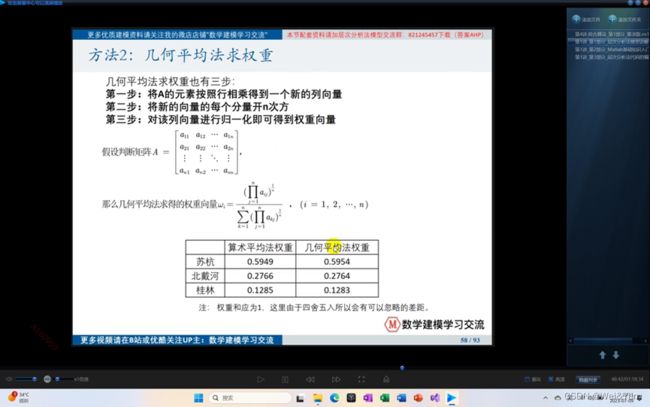
2.几何平均法求权重
3.特征值法求权重
- MATLAB基本语法函数以及层次分析法的实现
（博主是计算机专业所以很多语法函数会与c/cpp中的语法做比较方便计算机专业的理解）
- Matlab中的每个语句不需要必须加 ‘ ；’ ，若加上分号表示在执行中此语句执行但不显示出来，若不加分号则执行后语句结果会在命令行窗口（c中的控制台）显示
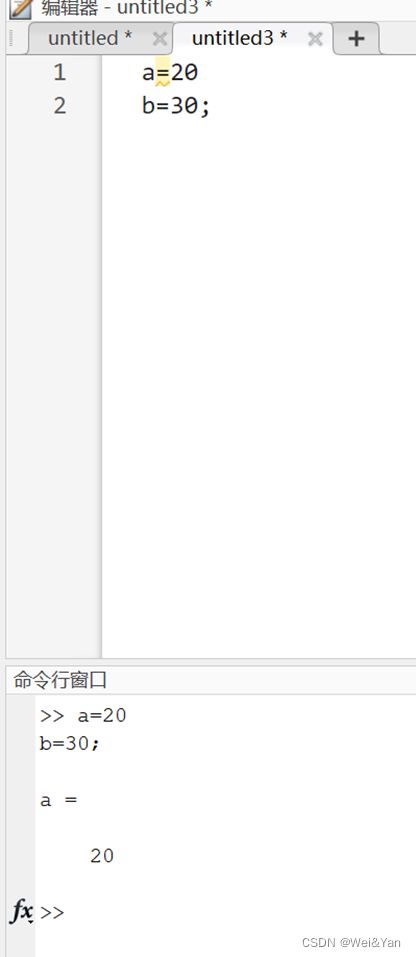
（两个语句都执行了却只显示了a=20）
2.注释：matlab中的注释符号是%（类似c中的//）
3.matlab中的命令行窗户（c中的控制台）和工作区（c中监视区的监视变量）每次执行后都会有保存，不会清空，所以使用clear（清楚工作区）clc（清除命令行窗口）
clear；clc 平时都会这样两个连用清楚所有：起到了初始化的作用，防止之前的结果对新的脚本产生干扰
4输入函数disp（）
（）中为要输出的内容，若为字符串需要用“”/’’引起来（类似c/cpp中的printf，cout）
注意：disp后面加不加；都会输出
5.向量（c中数组）一般赋值矩阵使用，为了方便理解我们成为矩阵。
矩阵中间列的符号是“ ,”（英文逗号）“ ”（空格）
间隔行的符号是“；”（分号）
Eg:
6.合1并字符串
a.strcat函数 strcat（‘str1’,’str2’）
b. [‘str1’,’str2’](看成一个数组)
7.num2str（）将数字转换成字符串（因为直接把数字当字符串输出会根据ASCII码转换成对应的字符如：97对应‘a’）
如果使用disp（）函数输出的时候在disp括号中直接把数字转换成字符串且与已有字符串相连接
8.输入函数 intput（）（类似与c中的scanf）
9.求和函数sum（），若括号中为矩阵，默认只输入矩阵是按列求和，最后得到一个一列n行的向量。Sum（A，1）后面加1是按列求和sum（A，2）后面加2是按行求和
10.提取矩阵中指定位置元素
a.取指定行和列A（行，列）
b.取某一行A（行，：）加冒号
c.取某一列A（：，列）
d取某写全部元素A（[2,5],:）取第二行和第五行
补充matlab中的等差数列 a1 : d : max(max是数列能取到的最大范围)
如果不加d则默认d为1。
e．取全部元素A（ ：）
11.size（）函数求矩阵的行和列
Size（A，1）返回行size（A，2）返回列
12.repmat（）函数复制矩阵函数
B=remat（A，2，1）将A矩阵赋值两行A，一列A成为一个新的矩阵B
13．矩阵之间的运算
* /是矩阵的* /。.* ./是矩阵中对应的每个元素相互*/。
14.开方 ^ a^n意味a的n次方（同样应用于矩阵，若相对矩阵中每个元素开方应用 .^）
15.eig(A)求矩阵的特征值和特征向量的函数
[V,D]=eig(A) V表示特征向量 D表示特征值（若只有一个接收则只返回特征值）
16.find（）函数 返回向量或矩阵中不为0的元素的下标
若后面加数字n则表示返回前n个不为0的元素。
若x为矩阵：
[r,c]=find(x)
r：位置不为0的元素的行坐标
c：位置不为0的元素的列坐标
17.矩阵中判断大小关系：
> < == ~=(对应c中的> ,< ,== ,!=)
返回一个logical数组（其中元素为1代表符合条件，为0不符合）
18.判断语句
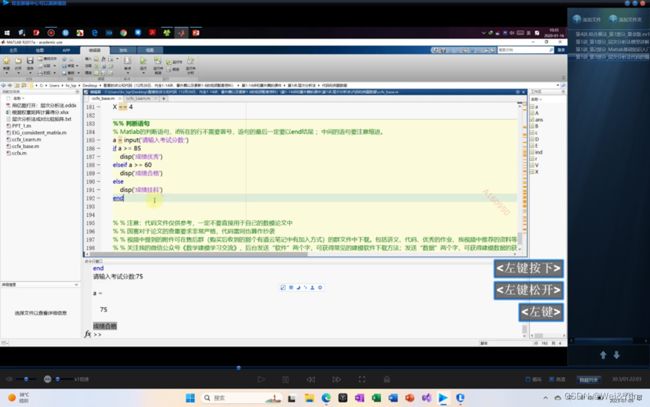
19.for循环(一定要以end结尾)
For i=1：10（等同于c中的for（int i=1;i<=10;i++））
~~
~~
End
20.相乘函数prod（）后面加1为按列相乘，加2为按行相乘
21.ones与zeros函数
层次分析法matlab代码的实现
算数平均法求权重
%填入方形矩阵
A=[1,1,4,1/3,3;
1,1,4,1/3,3;
1/4,1/4,1,1/3,1/2;
3,3,3,1,3;
1/3,1/3,2,1/3,1]
%求出矩阵每列的和
SUM_A=sum(A)
%求出矩阵的行数
n=size(A,1)
%将求出来的每列的和扩大n行倍，方便归一化（每个元素除以其所在列的和）
SUM_cA=repmat(SUM_A,n,1)
%第一步归一化处理
A_guiyi=A./SUM_cA
%第二部将归一化元素各列相加（按行求和得到一个列向量）
SUM_guiyiA=sum(A_guiyi,2)
LAST_A=SUM_guiyiA./n几何平均法求权重
%填入方形矩阵
A=[1,1,4,1/3,3;
1,1,4,1/3,3;
1/4,1/4,1,1/3,1/2;
3,3,3,1,3;
1/3,1/3,2,1/3,1]
%第一步将A元素各行相乘得到一个列向量
Prod_A=prod(A,2)
%第二部将新向量中每个元素开n次方（成1/n次方）
Prod_nA=Prod_A.^(1/n)
%将开n次方后的向量归一化处理得到权重(归一化就是将向量中的每个元素除向量和)
disp('几何平均法求权重结果：')
disp(Prod_nA/sum(Prod_nA))特征值法求权重
%填入方形矩阵
A=[1,1,4,1/3,3;
1,1,4,1/3,3;
1/4,1/4,1,1/3,1/2;
3,3,3,1,3;
1/3,1/3,2,1/3,1]
%第一步求出A的最大特征值，以及其对应的特征向量(V向量，Val值)
[V,val]=eig(A)
%求最大特征值
MAX_val=max(max(val))%第一个max求每列的最大特征值第二个求真个矩阵最大特征值
%求最大特征值对应的特征向量
% 1.找到最大特征值的位置，并保存它的位置
[r,c]=find(val==MAX_val,1)
%2.（***）求出列所在那一行的向量就是最大特征值向量
V(:,c)
%第二步对求出的特征向量进行归一化处理（让最大特征向量的每个元素除其和）得到我们的权重
disp('特征值法求权重的结果为')
disp(V(:,c)./sum(V(:,c)))博主主要跟着清风数学建模的课程学习，其中里面的一些图片都来源于上课视频的截图。