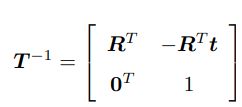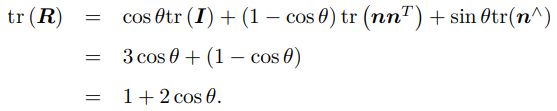【SLAM14讲】04 三维空间刚体运动
一、坐标系之间的欧式变换
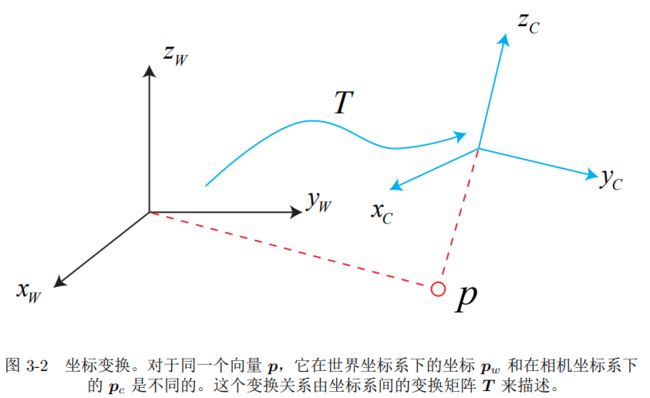
xW , yW , zW定义的世界坐标系,xC , yC , zC 定义的相机坐标系。
相机视野中某个向量 p,它的坐标为pc,而从世界坐标系下看,它的坐标 pw。
二、相机运动
相机运动是一个刚体运动,它保证了同一个向量在各个坐标系下的长度和夹角都不会发生变化,这种变换称为欧氏变换。这样一个欧氏变换由一个旋转R和一个平移t两部分组成。
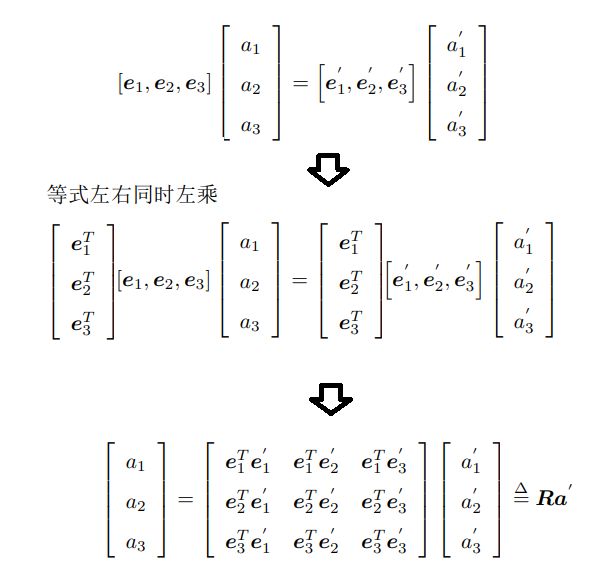
这里考虑旋转。我们设某个单位正交基 (e1, e2, e3) 经过一次旋转,变成了 (e ′ 1 , e ′ 2 , e ′ 3 )。它在两个坐标系下的坐标为 [a1, a2, a3] T 和 [a ′ 1 , a ′ 2 , a ′ 3 ] T。 根据坐标的定义,有:
- 矩阵R称为旋转矩阵,由两组基之间的内积组成,刻画了旋转前后同一个向量的坐标变换关系,是一个行列式为 1 的正交矩阵。
- 旋转矩阵的逆(即转置)描述了一个相反的旋转
- 旋转矩阵的集合定义如下
SO(n) 是特殊正交群
这里的变换关系不是一个线性关系。假设我们进行了两次变换:R1, t1 和 R2, t2:
这样的形式在变换多次之后会过于复杂,于是重写:
- 把一个三维向量的末尾添加 1,变成了四维向量,称为齐次坐标。
对于这个四维向量,我们可以把旋转和平移写在一个矩阵里面,使得整个关系变成了线性关系。该式中,矩阵 T 称为变换矩阵(Transform Matrix)。用 a˜ 表示a的齐次坐标。
- 在齐次坐标中,某个点 x 的每个分量同乘一个非零常数 k 后,仍然表示的是同一个点。
因此,一个点的具体坐标值不是唯一的。如 [1, 1, 1, 1]T 和 [2, 2, 2, 2]T 是同一个点。但当最后 一项不为零时,我们总可以把所有坐标除以最后一项,强制最后一项为 1,从而得到一个 点唯一的坐标表示。
忽略掉最后一项,这个点的坐标和欧氏空间就是一样的。
经重写后:
变换矩阵 T,它具有比较特别的结构:左上角为旋转矩阵,右侧为平移向量,左 下角为 0 向量,右下角为 1。这种矩阵又称为特殊欧氏群。
解该矩阵的逆表示一个反向的变换:
三、旋转向量
任意旋转都可以用一个旋转轴和一个旋转角来刻画。于是,我们可以使用一个向量,其方向与旋转轴一致,而长度等于旋转角。这种向量,称为旋转向量(或轴角)。旋转轴为 n,角度为 θ 的旋转,它对应的旋转向量为 θn。
旋转向量 --> 旋转矩阵的过程
由罗德里格斯公式(Rodrigues’s Formula ):
旋转矩阵 --> 旋转向量的过程
转角:
由于旋转轴上的向量在旋转后不发生改变,转轴 n:
转轴 n 是矩阵 R 特征值 1 对应的特征向量。
四、欧拉角
旋转矩阵、旋转向量,虽然它们能描述旋转,但对我们人类是非常不直观的。欧拉角则提供了一种非常直观的方式来描述旋转——它使用了三个分离的转角,把一个旋转分解成三次绕不同轴的旋转。比如说,当我先绕 X 轴旋转, 再绕 Y 轴,最后绕 Z 轴,就得到了一个 XYZ 轴的旋转。
欧拉角的一个重大缺点是会碰到著名的万向锁问题(Gimbal Lock):在俯仰角为 ±90◦ 时,第一次旋转与第三次旋转将使用同一个轴,使得系统丢失了一个自由度(由三次旋转变成了两次旋转)。
五、四元数
复数集 C 表示复平面上的向量,而复数的乘法则能表示复平面上的旋转:例如,乘上复数 i 相当于逆时针把一个复向量旋转 90 度:
(a + bi)i = -b + ai 旋转90°
(a + bi)i*i 旋转180°
(a + bi)(
) 旋转45°
在表达三维空间旋转时,也有一种类似于复数的代数:四元数(Quaternion)。四元数是Hamilton 找到的一种扩展的复数. 它既是紧凑的,也没有奇异性。如果说缺点的话,四元数不够直观,其运算稍为复杂一些。
5.1 四元数
一个四元数 q 拥有一个实部和三个虚部:
其中 i, j, k 为四元数的三个虚部。这三个虚部满足关系式:
用一个标量和一个向量来表达四元数:
s 称为四元数的实部,而 v 称为它的虚部。如果一个四元数虚部为 0,称之为实四元数。反之,若它的实部为 0,称之为虚四元数。
六、对比
1、旋转矩阵
- 自身带有约束:它必须是个正交矩阵,且行列式为 1。
- SO(3) 的旋转矩阵有九个量,但一次旋转只有三个自由度。因此这种表达方式是冗 余的。
2、变换矩阵
- 自身带有约束:它必须是个正交矩阵,且行列式为 1。
- SE(3) 的旋转矩阵有16个量,但一次旋转只有三个自由度。因此这种表达方式是冗 余的。
3、欧拉角和旋转向量是紧凑的,但具有奇异性。
4、四元数(Quaternion)它既是紧凑的,也没有奇异性。如果说缺点的话,四元数不够直观,其运算稍为复杂一些。