矩阵svd分解和矩阵的伪逆
真该好好学习一下Latex数学公式的语法和规则了，否则，连写个博客都没法写，这叫什么事！
https://blog.csdn.net/ViatorSun/article/details/82826664
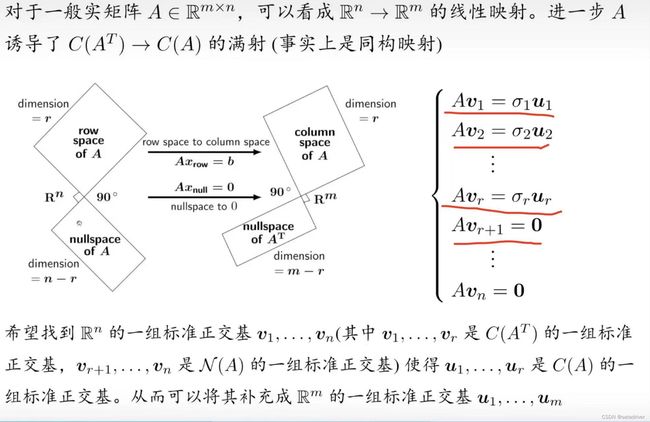
直接上数学博士写的ppt图（肯定比我在这里胡说八道强的多），知识放在这里，经得起推敲，自己慢慢琢磨去吧。
注意，第一张图中划线的部分是重点。得出该结论的前提是：A = U SIGMA (V^t)，因此 AV = U SIGMA，因为V 可以分解为多个向量，故A Vi = sigma U。
下面这种方式也可以，只不过是对上面的对称矩阵交换了一下顺序而已：
伪逆的定义：
