国赛培训——评价模型——层次分析法

例题

问题：填好志愿后，小明同学想出去旅游。在查阅了网上的攻略后，他初步选择了苏杭、北戴河和桂林三地之一作为目标景点。
请你确定评价指标、形成评价体系来为小明同学选择最佳的方案.
分析：本题为评价类问题，且决策层(指标)的数据未知，可以使用层次分析法建模。
（1）评价目标是什么：选择最合适的目标景点
（2）有哪几种可选方案：苏杭、北戴河和桂林
（3）评价的指标是什么：
通过在知网、万方数据库等平台查询，筛选得出如下五个的影响因素：景色、花费、居住条件、饮食、交通。
（4）建立层次结构模型
将决策问题分解为三个层次，最上层为目标层M，即选择最佳的目标景点。最下层为方案层，即可选方案。中间层为准则层，包括景色、花费、居住条件、饮食、交通五个决策指标。

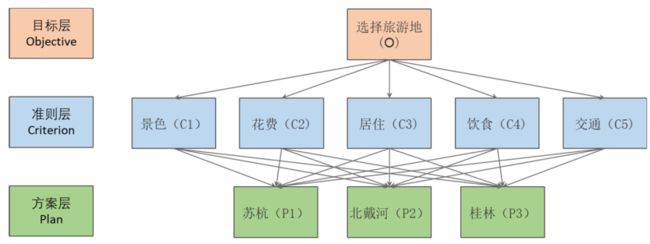
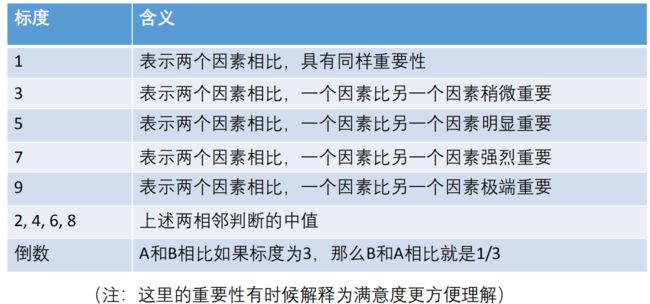
（5）设置权重
重要程度表用于指标间的两两比较：

层次分析法将有如下三类权重表格：
①打分表格（指标+目标）

②指标间判断矩阵（指标间的重要程度对比）

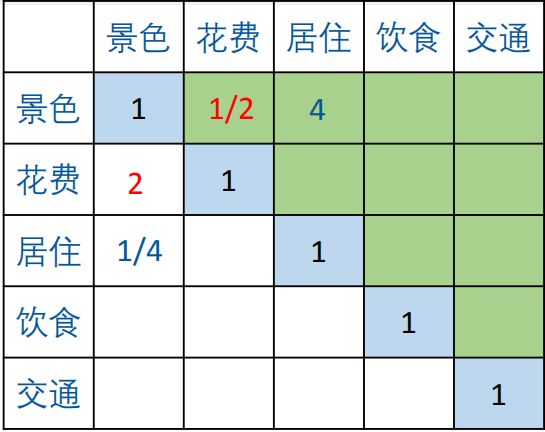
其中a_{ij}代表相对于指标j，i的重要程度。该矩阵是正互反矩阵。
③某一指标下的判断矩阵

其中b_{ij}代表方案i相对于方案j的满意程度。矩阵B是正互反矩阵。

第一步：填写指标间、与方案间判断矩阵


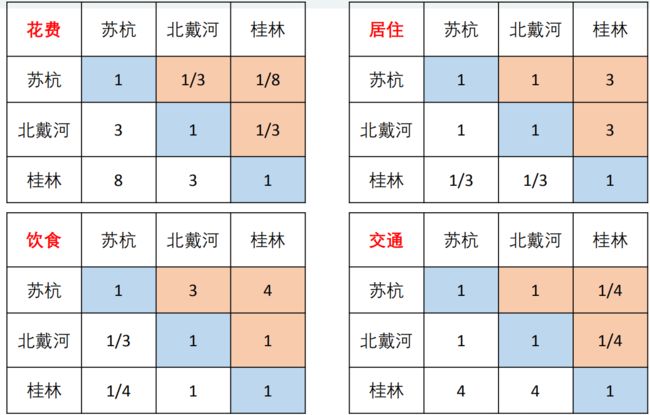
但是在景色下的案例权重矩阵中，出现了矛盾现象：景色方面苏杭>北戴河，北戴河>桂林，但是苏杭=桂林。与设置矛盾，此时应该考虑矩阵的一致性问题。

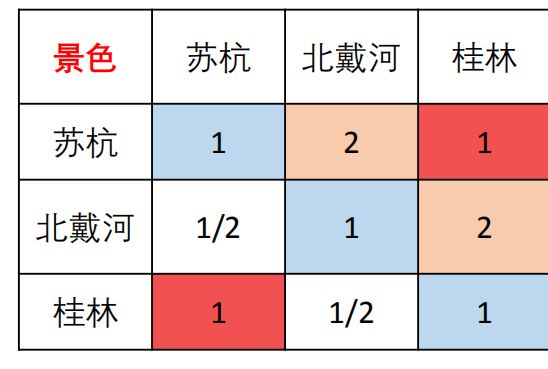
第二步：一致性检验
引理：n阶正互反矩阵A为一致性矩阵时当且仅当特征值λ=n。否则一定满足λ>n

①计算一致性指标CI

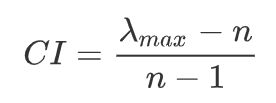
②查找对应的平均随机一致性指标RI

③计算一致性比例CR

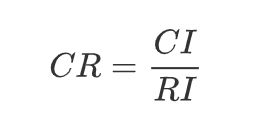
当CR < 0.1时，可以认为矩阵的一致性可以接受；否则需要对判断矩阵进行修正。（修正方法可以根据一致矩阵的行列间数据成比例进行修改）
max()和max(max())的区别
对于矩阵max()返回包含最大值的行，而max(max())返回矩阵中的最大值

%{
max_eig:最大特征值
D：由全部特征值构成的对角阵
%}
disp('请输入判断矩阵A')
A=input('A=');
[n n] = size(A);
[V D] = eig(A);
max_eig = max(max(D));
CI = (max_eig - n)/(n-1);  %第一步：CI
RI = [0 0.0001 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59]; %第二步：RI
CR = CI/CR(n);  %第三步：CR
disp('一致性指标CI=');disp(CI);
disp('一致性比例CR=');disp(CR);
if CR<0.10
    disp('因为CR<0.10，所以该判断矩阵A的一致性可以接受!');
else
    disp('注意：CR >= 0.10，因此该判断矩阵A需要进行修改!');
end

通过一致性检验与修正，将景色内方案间权值修改为：

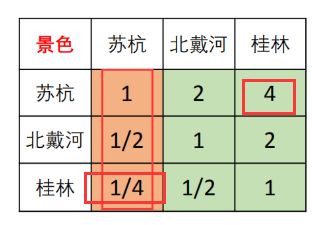
（6）计算权值
引理：A为n阶方阵，且r(A)=1,则A有一个特征值为tr(A)，其余特征值均为0.因此一致矩阵的各行成比例且不是零矩阵，所以一致矩阵的秩一定为1.

6.1 一致矩阵计算权值
根据引理可知，一致矩阵的特征值为n，对应的特征向量刚好是一致矩阵的第一列。

6.2 非一致性矩阵计算权值
方法一：算数平均法
①将判断矩阵按列归一化
②将归一化的各列相加并除以n得到权重向量

%{
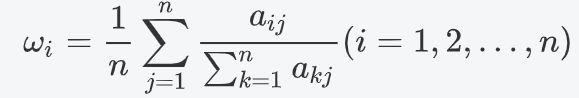
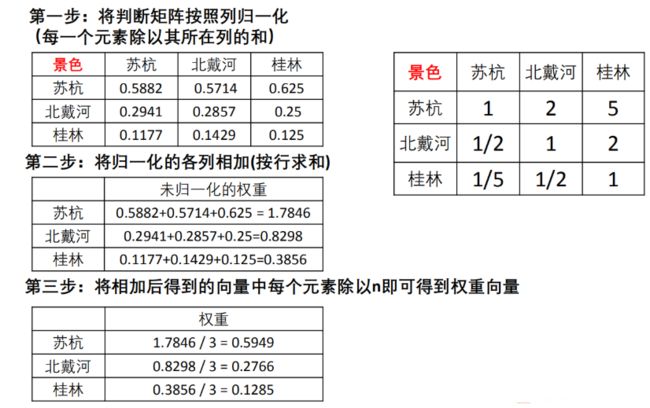
disp('请输入判断矩阵A')
A=input('A=');
[n,n] = size(A);
%}
sum_A = sum(A); %得到1*n的向量,对应每一列的和
SUM_A = repmat(sum_A,n,1);
w = A ./ SUM_A;   % ./

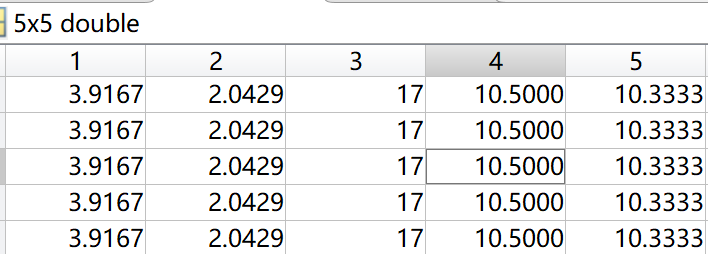
其中一个具体的SUM_A实例如下：

方法二：几何平均法
①将矩阵按行相乘得到新的列向量
②新的列向量每个分量开n次方
③对列向量进行归一化

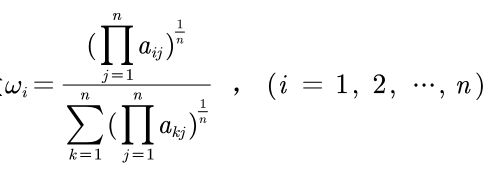
prod(A,dim)用法
dim=1时，按列乘积并返回1n的行向量
dim=2时，按行乘积并返回n1的列向量

%{
disp('请输入判断矩阵A')
A=input('A=');
[n,n] = size(A);
%}
product_A = prod(A,2);
PRODUCT_A = product_A .^ (1/n);
disp('几何平均法求权重的结果为：');
disp(Prduct_n_A ./ sum(Prduct_n_A))

方法三：特征值法求权重
①求出矩阵的最大特征值以及对应的特征向量
②对特征向量进行归一化得到权重


find(A,x)返回满足条件A中前x个的位置

[V D] = eig(A);
max_eig = max(max(D));
[r c] = find(D==max_eig , 1);
disp('特征值法求权重的结果为：');
disp( V(:,c) ./ sum(V(:,c)) )

其中特征向量V如图所示：某一列代表某一个特征值对应的特征向量

一般同时使用三种方法计算权值

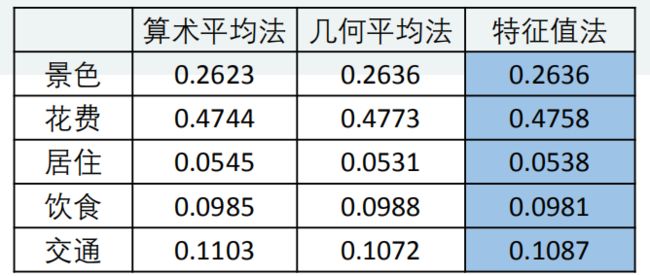
为了保证结果的稳健性，本文采用了三种方法分别求出了权重后计算平均值，再根据得到的权重矩阵计算各方案的得分，并进行排序和综合分析，这样避免了采用单一方法所产生的偏差，得出的结论将更全面、更有效。

（7）计算得分并进行排序
将上述六个判断矩阵（指标间权重矩阵1+指标内案例权重矩阵5）得到的权重填入表格，并通过在EXCEL中计算权值得分。

	指标权重	苏杭	北戴河	桂林
景色	0.2636	0.5954	0.2764	0.1283
花费	0.4758	0.0819	0.2363	0.6817
居住	0.0538	0.4286	0.4286	0.1429
饮食	0.0981	0.6337	0.1919	0.1744
交通	0.1087	0.1667	0.1667	0.6667
得分		0.2811	0.2271	0.3829

Excel计算公式：=C2*$B$2+C3\ast$B$3+C4\ast$B$4+C5\ast$B$5+C6*H5。 通过F4锁定权值项拖拉得解。

由此可知桂林>苏杭>北戴河，因此选择桂林作为目标地点。

一些局限性

（1）评价的决策层不能太多，太多的话n会很大，判断矩阵和一致矩阵差异会很大。
（2）如果决策层中指标的数据已知，此时层次分析法并不是一个能精确评价的好方法。

代码

clc,clear;
%1.输入判断矩阵
disp('请输入判断矩阵A')
A = input('A=');
[n n] = size(A);

%2.三种方法计算权重
%方法一：算数平均法计算权值
sum_A = sum(A);  %n*1
SUM_A = repmat(sum_A,n,1);  %n*n
w = A ./SUM_A;
disp('算术平均法求权重的结果为：');
disp(sum(w,2) ./n)
%按行相加并除以n得到权重向量n*1
%方法二：几何平均法计算权值
prod_A = prod(A,2);  %按列相乘
PROD_A = prod_A .^ (1/n);
disp('几何平均法求权重的结果为：');
disp(Prduct_n_A ./ sum(Prduct_n_A))
%方法三：特征值计算权重
[V D] = eig(A); %V特征向量 D特征值
max_eig = max(max(D));  %最大特征值
[r c] = find(D==max_eig,1);
disp('特征值法求权重的结果为：');
disp(V(:,c) ./ sum(V(:,c)))  %对应特征向量计算

%3. 一致性检验
CI = (max_eig - n) / (n-1);
RI=[0 0.0001 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];  
CR=CI/RI(n);
disp('一致性指标CI=');disp(CI);
disp('一致性比例CR=');disp(CR);
if CR<0.10
    disp('因为CR<0.10，所以该判断矩阵A的一致性可以接受!');
else
    disp('注意：CR >= 0.10，因此该判断矩阵A需要进行修改!');
end

Reference

清风数学建模：
https://www.bilibili.com/video/BV1DW411s7wi