论文笔记-粗读-8.22~8.29
01-Learning Structured Sparsity in Deep Neural Networks
原文:https://arxiv.org/pdf/1608.03665.pdf
代码:https://github.com/wenwei202/caffe/tree/scnn

文章采用结构化稀疏的方法对不同的结构进行修剪。最终将20层的ResNet修剪至18层,同时精度由92.25%提升至92.60%。
- filters和channels之间存在冗余[11];
- filters为什么一定是正方形呢?
- 深度网络有时因为梯度爆炸和梯度消失的问题而不能够reach the expected accuracy[5];
受以上事实的启发,文章提出了SSL来直接习得压缩的网络结构。SSL采用训练时的group lasso,并且是一个通用的正则方法,能够针对filters, channels, 每层的fiter shapes, layer depth等多种结构层次进行调节。
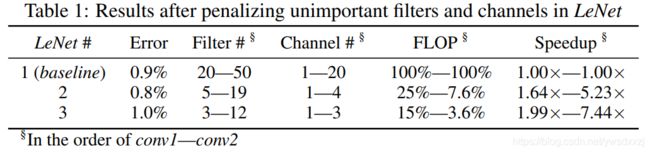
(这个通用性值得肯定,然而本文实现的剪枝率和非结构化剪枝相比并不算优秀,如下:
02-Manifold Regularized Dynamic Network Pruning
原文:https://export.arxiv.org/pdf/2103.05861
代码:https://github.com/yehuitang/Pruning/tree/master/ManiDP
精读笔记:https://blog.csdn.net/ywsdxxzj/article/details/119847687
本文从复杂性和相似性发掘了样本空间的流型信息,并使用了一个自适应的惩罚来使得的样本复杂度和网络复杂度相匹配。
本文首先引入了一种判断输入图像复杂度并且适宜地调整filters稀疏的惩罚程度的机制,其次,在剪枝结果中保存了样本间的相似性。
本文实现的结果是:ResNet-34在ImageNet上实现了55.3%的FLOPs减少,代价是0.57%的top-1 accu损失。
03-Dynamic Channel Pruning: Feature Boosting and Suppression
原文:
代码:
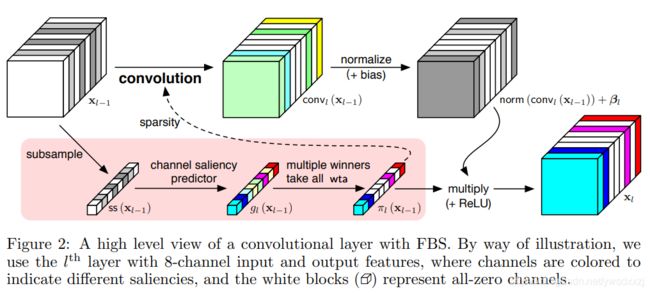
本文是run-time pruning的典型(亦称dynamic pruning)。采用一个单层的小网络,将每个channels的信息(采用L1范数,L2范数或者方差简化为标量,即 R C ∗ H ∗ W → R C R^{C*H*W} \xrightarrow{} R^{C} RC∗H∗WRC)作为输入,以产生输出作为评判不同filters重要程度的依据。
讲道理,没太明白这个辅助网络↓要怎么调参。
g l ( x l − 1 ) = ( s s ( x l − 1 ) + ρ l ) + g_{l}(\bold{x}_{l-1})=(ss(\bold{x}_{l-1})+\bold{\rho}_{l})_{+} gl(xl−1)=(ss(xl−1)+ρl)+
04-Efficient Online and Batch Learning Using Forward Backward Splitting
采用次梯度方法,对损失函数于与可微(?)惩罚分两步求解。
05-Directional Pruning of Deep Neural Networks
原文:https://arxiv.org/pdf/2006.09358v2.pdf
代码:https://github.com/donlan2710/gRDA-Optimizer/tree/master/directional_pruning
本文采用的是非结构化的稀疏正则化方法。
作者注意到梯度下降SGD收敛到某点 w S G D w^{SGD} wSGD时,其海森矩阵经常会有许多近零的特征值,那么沿着这些特征值对应的特征向量的方向修建时,就不会造成太大的精度损失。本文将这种剪枝方法命名为directional pruning。
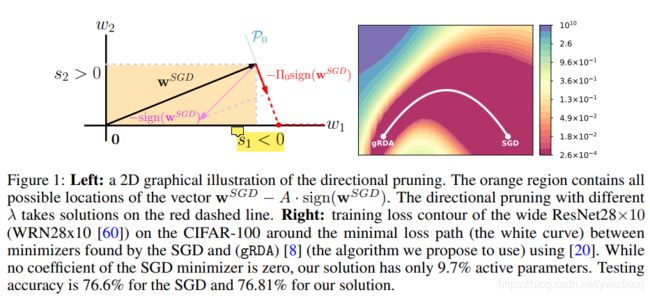
麻烦的是随着权重维度的增长,海森矩阵的计算难度将爆炸式上升。因此本文研究了一种简单的算法——gRDA,无需计算二阶导数,只需增加一个时变的惩系数即可达到目的:
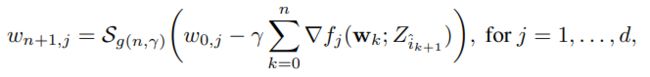
其中, g ( n , γ ) = c γ 1 2 ( n γ ) μ g(n, \gamma)=c\gamma^\frac{1}{2}(n\gamma)^{\mu} g(n,γ)=cγ21(nγ)μ, c , μ > 0 c, \mu>0 c,μ>0。
文章随后证明了渐进意义下gRDA在时间 t → ∞ t \to \infty t→∞时,gRDA的解 w g R D A ( t ) w_{gRDA}(t) wgRDA(t)是directional pruning的解 w ∗ w^{*} w∗的无偏估计。并通过实验验证了算法收敛时 ∣ ∣ w g R D A ( t ) − w ∗ ∣ ∣ ||w_{gRDA}(t)-w^{*}|| ∣∣wgRDA(t)−w∗∣∣的值非常小,这说明此算法确实达到了directional pruning的效果。
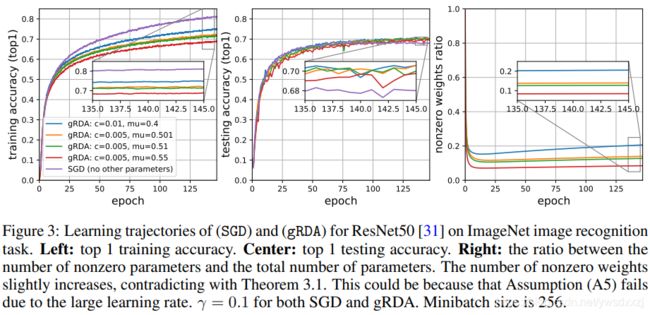
文章实现了比较高的剪枝率,尤其是对ImageNet上的ResNet-50剪枝时,几乎所有 c , μ c, \mu c,μ的取值组合都表现出了比SGD更好的泛化能力,这值得注意:
06-An Entropy-based Pruning Method for CNN Compression
原文:http://export.arxiv.org/pdf/1706.05791
代码:略
一篇filters粒度的静态剪枝方法,采用输出特征图L1范数的信息熵来度量不同filters的重要性程度。
07-Pruning neural networks without any data by iteratively conserving synaptic flow
原文:https://arxiv.org/pdf/2006.05467.pdf
代码:https://github.com/ganguli-lab/Synaptic-Flow
解决的问题
- 现有的gradient-based的剪枝方法在初始化时会遭遇layer-collapse的问题——即导致过早的剪去一整个layer使得网络模型无法训练的现象;
- 彩票假设提出后,对模型到底是否需要pre-trained提出了质疑,很自然有这样一个问题:能不能不训练,甚至不借助于任何数据输入,而直接地detect the wining lottery ticket? 对此目前没有有效的算法;
方法的新颖之处
- 不依赖于训练数据就能够识别wining ticket;
研究范围
在VGG, ResNet等模型,对于CIFAR-10/100和Tiny ImageNet等数据集。
效果
99.9%的最大稀疏率 (which means the accuracy drops exactly to zero).
贡献
- Maximal Critical Compression
- synaptic saliency
有意思的引文
本篇的related works部分比较全面,概括得很有条理,建议研究一下。
引文15, 16, 17-新颖的微架构设计
引文25-https://arxiv.org/pdf/2002.04809v1.pdf
引文29, 30, 31-基于更多复杂变量