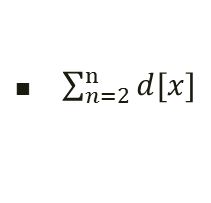并查集&最小生成树学习笔记

并查集：

并查集是一种可以动态维护若干个不重叠的集合，并支持合并与查询的数据结构。

Find(x)：查询元素x所在集合
Merge(x, y):将x所在集合与y所在集合合并

集合的表示方法：为每个集合选择一个固定的元素，作为这个集合的代表元。

实现：

用一棵树形结构存储每个集合，树上每个节点都是一个元素，树根是集合的代表元素。用fa[x]保存x的父亲节点，根的fa值为它本身。

合并两个集合时，只需要连接两个树根（即令一个树根为另一个树根的子节点，fa[x]=y）

路径压缩：

可以发现，我们只关心每个集合的代表元（即每棵树的根节点），而不关心这棵树的具体形态——这意味着下图两棵树是等价的。

因此我们可以在每次执行Find操作的同时，把访问过的每个节点都直接指向树根。
采用路径压缩优化的并查集，每次Find操作的均摊复杂度为O(logN)

代码：

初始化
for (int i=1; i<=n; i++) fa[i]=i;
Find
    int Find(int x) 	
    {
		if (x==fa[x]) return x;
		return fa[x]=Find(fa[x]);
    }
Merge
    	void Merge(int x ,int y)
    	  {
    		fa[Find(x)]=Find(y);
	      }

例题

HDU1232
某省调查城镇交通状况，得到现有城镇道路统计表，表中列出了每条道路直接连通的城镇。省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通（但不一定有直接的道路相连，只要互相间接通过道路可达即可）。问最少还需要建设多少条道路？
N<=1000;

题解：
每个城市是一个点，每修一条路就是将两个集合合并。
答案是即最后集合个数-1.

带权并查集：

并查集实际上是由若干棵树构成的森林，我们可以在树中的每条边上记录一个权值，即维护一个数组d，用d[x]保存节点x到父节点fa[x]之间的边权。

在每次路径压缩后，每个访问过的点都会直接指向树根，如果我们同时更新这些节点的d值，就可以利用路径压缩的过程来统计每个节点到树根之间的路径上的一些信息。

例题

NOI2002 银河英雄传说
有一个划分为N列的星际战场，各列以此编号为1,2,…,N。有N艘战舰，也依次编号为1,2,…,N，其中第i号战舰位于第i列。有M条指令，每条指令格式为以下两种之一：
M i j，表示让第i号战舰所在列的全部战舰保持原有顺序，接在第j号战舰所在列的尾部
C i j，表示询问第i号战舰与第j号战舰当前是否处于同一列中，如果在同一列中，他们之间隔了多少艘战舰。
N<=3e4,M<=5e5

题解：

M操作可以看做两个集合的合并
C操作中询问是否在同一列中即查询两个元素是否在同一个集合
中间隔了多少个战舰？
d[x]：x与fa[x]之间有多少个元素
如果x和y在一个集合中，abs(d[y]-d[x])-1即为答案。

代码：

Int Find(int x)
{
    if (x==fa[x]) return x;
    int root=Find(fa[x]);
    d[x]+=d[fa[x]];//权值相加
    return fa[x]=root;
}

void Merge(int x,int y)
{
    x=Find(x);
    y=Find(y);
    fa[x]=y;
    d[x]=size[y];		//size[y]=y集合内的元素
    size[y]+=size[x];		
}

扩展域并查集：

有些情况下，元素不只含有一个属性，传递的关系也不只一种。因此我们可以将每个元素拆成多个元素，在合并的时候维护关系的传递性，通过扩展出来的属性来维护传递性。

例题

POJ1182 食物链
有三种动物，A吃B，B吃C，C吃A。
现有N个动物，K句描述：
1 x y：x和y是同类
2 x y：x吃y
符合下列三个条件之一的即为错误语句，输出错误语句个数。
1.自己吃自己
2.x > n || y > n
3.当前语句和之前的正确语句发生了冲突

题解：

错误1和2可以显然的判定
将每个动物x拆成3个节点：
x_self：x的同类; x_eat：x可以捕食的；x_enemy：x的天敌

对于描述1 ：x和y是同类，则x和y的三种属性都是相同的
如果x_eat与y_self在一个集合(x吃y)或者x_self和y_eat在一个集合(y吃x)，则这句话是错误的。
合并x_self和y_self，x_eat和y_eat，x_enemy和y_enemy

对于描述2：x吃y，x是y的天敌
如果x_self和y_self在一个集合(x和y是同类)或者x_self和y_eat在同一集合(y吃x)，则这句话是错误的。
合并x_eat和y_sele，x_self和y_enemy，x_enemy和y_eat

代码：

#include 
#include 
#include 
#include 
using namespace std;
const int N=150005;
int fa[N];
int Find(int n)
{
    if(n==fa[n]) return n;
    return fa[n]=Find(fa[n]);
}
void change(int a,int b)
{
    fa[Find(a)]=Find(b);
}
int main()
{
    //freopen("a.txt","r",stdin);
    int n,m;
    scanf("%d %d",&n,&m);
    for(int i=1; i<=3*n; i++) fa[i]=i;
    int ans=0;
    for(int i=0; in || c>n || (a==2 && b==c))
        {
            ans++;
            continue;
        }
        int bet=b+n,ben=b+2*n,cet=c+n,cen=c+2*n;
        if(a==1)
        {
            if(Find(bet)==Find(c) ||Find(cet)==Find(b) ) ans++;
            else
            {
                fa[Find(b)]=Find(c);
                fa[Find(bet)]=Find(cet);
                fa[Find(ben)]=Find(cen);
            }
        }
        else if(a==2)
        {
            if(Find(b)==Find(c) ||Find(ben)==Find(c) ) ans++;
            else
            {
                fa[Find(bet)]=Find(c);
                fa[Find(cen)]=Find(b);
                fa[Find(ben)]=Find(cet);
            }
        }
    }
    printf("%d\n",ans);
    return 0;
}

最小生成树：

概念：

加权无向图是一种在无向图的基础上,为每条边关联一个权值或是成本的图模型.应用可以有很多:例如在一幅航空图中,边表示导线,权值则表示导线的长度或是成本等.
图的生成树是它的一颗含有其所有顶点的无环连通子图,一幅加权图的最小生成树(MST)是它的一颗权值(树中的所有边的权值之和)最小的生成树.下图为一幅加权无向图和它的最小生成树.(箭头不指示方向,标红的为最小生成树).

定理：
任意一棵最小生成树一定包含无向图中权值最小的边。

推论：
如果某个连通图属于最小生成树，那么所有从外部连接到该连通图的边中的一条最短的边必然属于最小生成树。

Kruskal：

维护无向图的最小生成森林，最初可认为生成森林由零条边组成。
在任意时刻，从剩余的边中选出一条权值最小的，并且这条边的两个端点不连通，把该边加入森林。

具体流程

建立并查集，每个点是一个集合
把所有边按照权值从小到大排序，依次扫描每条边(x,y,z)
若x,y属于同一集合，则忽略这条边，继续扫描下一条
否则，合并x和y所在的集合，并把z累加到答案中
添加了n-1条边后结束
复杂度O(mlogm)

代码：

int Kruskal()
 {
	for (int i=1;i<=n;i++) fa[i]=i;
	sort(edge+1,edge+1+m);
	for (int i=1;i<=m;i++)  {
		int x=Find(edge[i].x),y=Find(edge[i].y);
		if (x==y) continue;
		fa[x]=y;
		ans+=edge[i].z; // x y 为一条边的两个点，z为权值
	}
	return ans;
}

Prim：

维护最小生成树的一部分，最初仅确定1号点属于最小生成树。

在任意时刻，设已经确定属于最小生成树的节点集合为T，剩余节点集合为S，找到两个端点分别属于集合S，T的权值最小的边(x,y,z)，然后把点x从集合S中删除，加入到集合T，并把z累加到答案中。

复杂度O(n^2) 可用堆优化到O(mlogn)

主要用于稠密图尤其是完全图

具体流程：

d[x]：若x∈S，表示x与T集合中节点权值最小的边的权值，否则，表示x被加入T集合时选中的边的权值

用一个数组标记节点是否属于T，开始只有节点1属于T
每次从未被标记的节点中选出d值最小的，把它标记；同时扫描它的所有出边，更新到另一个端点的d值

答案为

代码：

void Prim()
{
    d[1]=0;
    for (int i=1; i<=n; i++)
    {
        int x=0;
        for (int j=1; j<=n; j++)
            if (!v[j] && (x==0||d[j]

例题

Bzoj1601 灌水

Farmer John已经决定把水灌到他的n块农田，农田被数字1到n标记。把一块土地进行灌水有两种方法，从其他农田饮水，或者这块土地建造水库。建造一个水库需要花费wi，连接两块土地需要花费Pij。计算Farmer John所需的最少代价。
N<=300, 1<=wi<=100000, (1<=pij<=100000,pij=pji,pii=0).

分析：

建立一个超级源点，每个点向源连权值为wi的边，其他任意两点之间连权值为pij的边，最小生成树即为答案。