新学虚树,写篇文章仔细地回顾一下吧。。。这玩意花了挺长时间的。
什么是虚树
虚树常常被使用在树形 dpdpdp 中,就比如这题。当一次询问仅仅涉及到整颗树中少量结点时,为每次询问都对整棵树进行 dpdpdp 在时间上是不可接受的。此时,我们建立一颗仅仅包含部分关键结点的虚树,将非关键点构成的链简化成边或是剪去,在虚树上进行 dpdpdp 。
虚树包含所有的询问点及它们之间的 lcalcalca 。显然虚树的叶子节点必然是询问点,因此对于某次含有 kkk 个点的询问,虚树最多有 kkk 个叶子结点,从而整颗虚树最多只有 2k−12k-12k−1 个结点(这会在虚树变成二叉树形态时达到)。
建立虚树之前
我们需要:
预处理出原树的 dfsdfsdfs 序以及 dpdpdp 可能用到的一些其他东西。
高效的在线 LCALCALCA 算法,单次询问 O(logn)O(logn)O(logn) 的倍增和树剖, O(1)O(1)O(1) 的 RMQ−STRMQ-STRMQ−ST 皆可。
将询问点按 dfsdfsdfs 序排序。
如何建立虚树
最右链是虚树构建的一条分界线,表明其左侧部分的虚树已经完成构建。我们使用栈 stakstakstak 来维护所谓的最右链, toptoptop 为栈顶位置。值得注意的是,最右链上的边并没有被加入虚树,这是因为在接下来的过程中随时会有某个 lcalcalca 插到最右链中。
初始无条件将第一个询问点加入栈 stakstakstak 中。
将接下来的所有询问点顺次加入,假设该询问点为 nownownow , lclclc 为该点和栈顶点的最近公共祖先即 lc=lca(stak[top],now)lc=lca(stak[top],now)lc=lca(stak[top],now) 。
由于 lclclc 是 stak[top]stak[top]stak[top] 的祖先, lclclc 必然在我们维护的最右链上。
考虑 lclclc 和 stak[top]stak[top]stak[top] 及栈中第二个元素 stak[top−1]stak[top-1]stak[top−1] 的关系。
情况一
lc=stak[top]lc=stak[top]lc=stak[top] ,也就是说, nownownow 在 stak[top]stak[top]stak[top] 的子树中
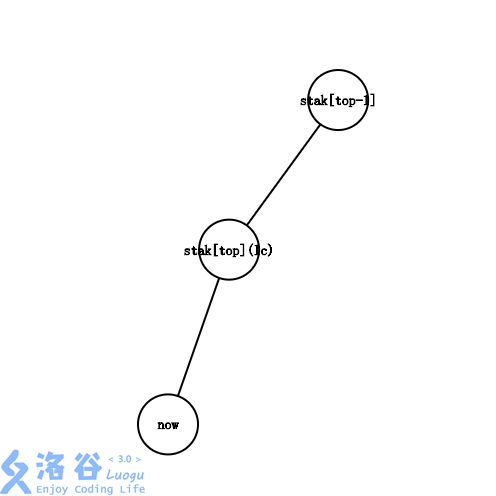
这时候,我们只需把 nownownow 入栈,即把它加到最右链的末端即可。
情况二
lclclc 在 stak[top]stak[top]stak[top] 和 stak[top−1]stak[top-1]stak[top−1] 之间。
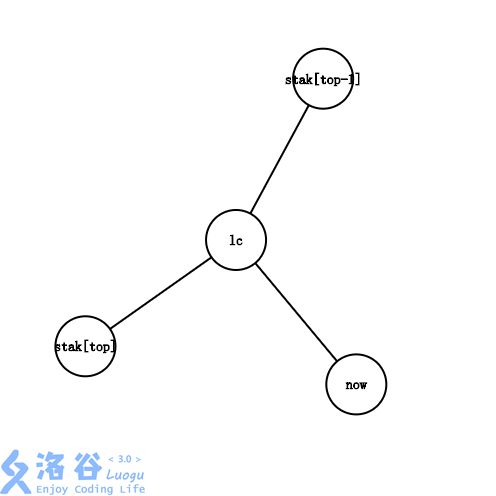
显然,此时最右链的末端从 stak[top−1]−>stak[top]stak[top-1]->stak[top]stak[top−1]−>stak[top] 变成了 stak[top−1]−>lc−>stak[top]stak[top-1]->lc->stak[top]stak[top−1]−>lc−>stak[top] ,我们需要做的,首先是把边 lc−stak[top]lc-stak[top]lc−stak[top] 加入虚树,然后,把 stak[top]stak[top]stak[top] 出栈,把 lclclc 和 nownownow 入栈。
情况三
lc=stak[top−1]lc=stak[top-1]lc=stak[top−1] 。
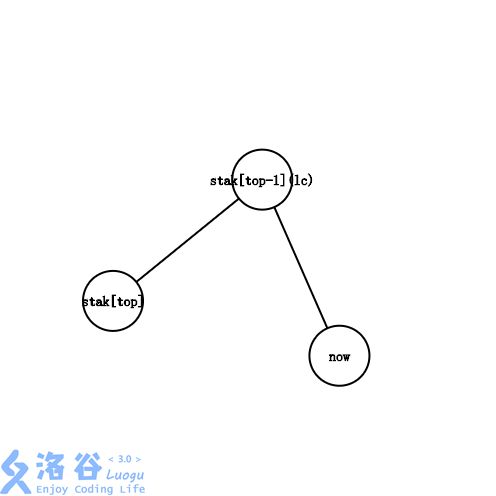
这种情况和第二种情况大同小异,唯一的区别就是 lclclc 不用入栈了。
情况四
此时有 dep[lc]dep[lc]<dep[stak[top−1]] 。 lclclc 已经不在 stak[top−1]stak[top-1]stak[top−1] 的子树中了,甚至也未必在 stak[top−2],stak[top−3]......stak[top-2],stak[top-3]......stak[top−2],stak[top−3]...... 的子树中。
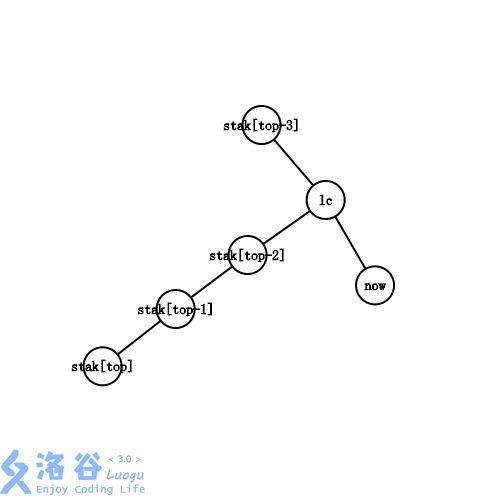
以图中为例,最右链从 stak[top−3]−>stak[top−2]−>stak[top−1]−>stak[top]stak[top-3]->stak[top-2]->stak[top-1]->stak[top]stak[top−3]−>stak[top−2]−>stak[top−1]−>stak[top] 变成了 stak[top−3]−>lc−>nowstak[top-3]->lc->nowstak[top−3]−>lc−>now 。我们需要循环依次将最右链的末端剪下,将被剪下的边加入虚树,直到不再是情况四。
就上图而言,循环会持续两轮,将 stak[top],stak[top−1]stak[top],stak[top-1]stak[top],stak[top−1] 依次出栈,并且把边 stak[top−1]−stak[top],stak[top−2]−stak[top−1]stak[top-1]-stak[top],stak[top-2]-stak[top-1]stak[top−1]−stak[top],stak[top−2]−stak[top−1] 加入虚树中。随后通过情况二完成构建。
#
当最后一个询问点加入之后,再将最右链加入虚树,即可完成构建。
一些问题
- 如果栈 stakstakstak 中仅仅有一个元素,此时 stak[top−1]stak[top-1]stak[top−1] 是否会出问题?
对于栈 stakstakstak ,我们从 111 开始储存。那么在这种情况下, stak[top−1]=0stak[top-1]=0stak[top−1]=0 ,并且 dep[0]=0dep[0]=0dep[0]=0 。此时 dep[lc]dep[lc]<dep[stak[top−1]] 恒成立。也就是说, stak[0]stak[0]stak[0] 扮演了深度最小的哨兵,确保了程序只会进入情况一和二。
- 如何在一次询问结束后清空虚树?
不能直接对图进行清空,否则复杂度会退化到 O(n)O(n)O(n) 的复杂度,这是我们无法承受的。在 dfsdfsdfs 的过程中每当访问完一个结点就进行清空即可。
回到本题
以样例的询问二为例(如下图)
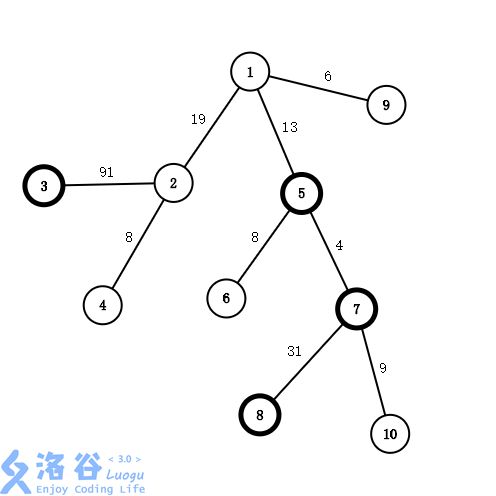
建立虚树是长这个样子的 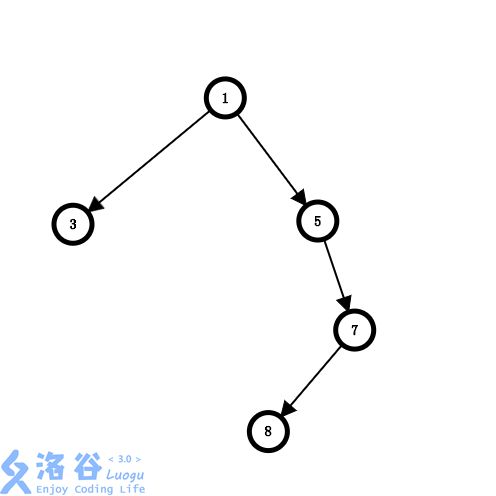
在本题中,建立有向树即可。我们预处理出 minv[pos]minv[pos]minv[pos] 代表从 111 到 pospospos 路径上最小的边权。如果 pospospos 是询问点,那么切断 pospospos 及其子树上询问点的最小代价 dp(pos)=minv[pos]dp(pos)=minv[pos]dp(pos)=minv[pos] ,否则,最小代价 dp(pos)=min(minv[pos],∑dp(to))dp(pos)=min(minv[pos],\sum dp(to))dp(pos)=min(minv[pos],∑dp(to)) (其中 tototo 是 pospospos 的儿子)。值得注意的是,即使 pospospos 是询问点,按道理用不到 dp(to)dp(to)dp(to) 的值,但仍旧需要对其儿子进行 dfsdfsdfs ,因为清空虚树需要对整个虚树进行遍历。
还有答案会爆 intintint ,所以不仅数组要开 LLLLLL ,初始化的 INFINFINF 也有必要开得足够大。我一开始直接拿 0x3f3f3f3f0x3f3f3f3f0x3f3f3f3f 结果 WAWAWA 了最后一个点。。。。
最后就是蒟蒻码风清奇常数巨大命名混乱的代码了
第一次写那么长的题解,以上内容均为口胡。由于自己实在是太蒟蒻了,错误缺漏之处在所难免,如有发现烦请各位大佬们指正。
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define mid ((l + r) >> 1)
#define Lson rt << 1, l , mid
#define Rson rt << 1|1, mid + 1, r
#define ms(a,al) memset(a,al,sizeof(a))
#define log2(a) log(a)/log(2)
#define _for(i,a,b) for( int i = (a); i < (b); ++i)
#define _rep(i,a,b) for( int i = (a); i <= (b); ++i)
#define for_(i,a,b) for( int i = (a); i >= (b); -- i)
#define rep_(i,a,b) for( int i = (a); i > (b); -- i)
#define lowbit(x) ((-x) & x)
#define IOS std::ios::sync_with_stdio(0); cin.tie(0); cout.tie(0)
#define INF 0x3f3f3f3f
#define LLF 0x3f3f3f3f3f3f3f3f
#define hash Hash
#define next Next
#define count Count
#define pb push_back
#define f first
#define s second
using namespace std;
const int N = 1e6+10, mod = 1e9 + 9;
const long double eps = 1e-5;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> PII;
typedef pair<ll,ll> PLL;
typedef pair<double,double> PDD;
template<typename T> void read(T &x)
{
x = 0;char ch = getchar();ll f = 1;
while(!isdigit(ch)){if(ch == '-')f*=-1;ch=getchar();}
while(isdigit(ch)){x = x*10+ch-48;ch=getchar();}x*=f;
}
template<typename T, typename... Args> void read(T &first, Args& ... args)
{
read(first);
read(args...);
}
int n, p;
int str[N], top;
int f[N][30];
int head[N], cnt;
ll mi[N];
int dep[N], dfn[N], idx;
int q[N];
vector<int> v[250010];
struct node {
int to, next, w;
} e[N];
inline void dfs(int u, int fa)
{
dep[u] = dep[fa] + 1;
f[u][0] = fa;
dfn[u] = ++ idx;
for(int i = head[u]; ~i; i = e[i].next)
{
int v = e[i].to;
if(v == fa) continue;
mi[v] = min((ll)e[i].w,mi[u]);
dfs(v,u);
}
}
inline void LCAinit()
{
dfs(1,0);
for(int j = 0; 1 << (j + 1) < n; ++ j)
for(int i = 1; i <= n; ++ i)
if(!f[i][j]) f[i][j + 1] = 0;
else f[i][j + 1] = f[f[i][j]][j];
}
inline int LCA(int u, int v)
{
if(dep[u] < dep[v]) swap(u,v);
int delta = dep[u] - dep[v];
for(int i = 0; (delta >> i) > 0; ++ i)
if(delta >> i & 1) u = f[u][i];
if(u == v) return u;
for(int i = log2(n); i >= 0; -- i)
if(f[u][i] != f[v][i])
u = f[u][i], v = f[v][i];
return f[u][0];
}
inline void add(int from, int to, int w)
{
e[cnt] = {to,head[from],w};
head[from] = cnt ++;
}
inline void add(int x,int y)
{
v[x].push_back(y);
}
inline bool cmp(int a, int b)
{
return dfn[a] < dfn[b];
}
inline void insert(int u)
{
if(top == 1) {str[++ top] = u; return;}
int lca = LCA(u,str[top]);
if(lca == str[top]) return;
while(top > 1 && dfn[lca] <= dfn[str[top - 1]])
{
add(str[top - 1], str[top]);
top --;
}
if(str[top] != lca) add(lca,str[top]), str[top] = lca;
str[++ top] = u;
}
inline ll dp(int x)
{
if(v[x].size()==0) return mi[x];
ll ans=0;
for(register int i=0;i<v[x].size();i++){
ans+=dp(v[x][i]);
}
v[x].clear();
return min(ans,mi[x]);
}
int main()
{
ms(head,-1);
ms(mi,LLF);
read(n);
for(int i = 0; i < n - 1; ++ i)
{
int l , r , w;
read(l,r,w);
add(l,r,w);
add(r,l,w);
}
LCAinit();
int m;
read(m);
while(m --)
{
int num;
read(num);
for(int i = 0; i < num; ++ i)
read(q[i]);
sort(q,q+num,cmp);
str[++ top] = 1;
for(int i = 0; i < num; ++ i) insert(q[i]);
while(--top) add(str[top],str[top + 1]);
cout << dp(1) << endl;
}
return 0;
}





