Codeforces Round #757 (Div. 2)——codeforces补题计划——2022.1.12&13

题目链接

A. Divan and a Store

题目大意：给出n个巧克力的单价分别是多少，给出买巧克力的最低价l, 最高价r, 以及总钱数，求最多能买多少。
贪心
排序，从符合范围的最低价开始买即可

#include 
using namespace std;
typedef long long LL;

int main(void)
{
    int  T;
    scanf("%d", &T);
    while(T --)
    {
       int n;
       scanf("%d", &n);
       vector<int> vec(n);
       int l, r, k;
       scanf("%d%d%d", &l, &r, &k);
       for(int i = 0; i < n; i ++)
       {
           scanf("%d", &vec[i]);
       }
       sort(vec.begin(), vec.end());
       int sum = 0;
       int ans = 0;
       for(int i = 0; i < n; i ++)
       {
           if(vec[i] >= l && vec[i] <= r && sum + vec[i] <= k)
           {
               sum += vec[i];
               ans ++;
           }
       }
       printf("%d\n", ans);
    }
    return 0;
}

B. Divan and a New Project

题目大意：给出n个点，给出去每个点的次数，现在要求重新排坐标，使得去各点距离 * 次数的和最小

思维、贪心
假设原点就是起点，按照次数排序，在原点两端分配，次数最高的排在距离原点最近即可。

#include 
#define x first
#define y second
using namespace std;
typedef long long LL;
typedef pair<LL, int> PII;
int main(void)
{
    int  T;
    scanf("%d", &T);
    while(T --)
    {
        int n;
        scanf("%d", &n);
        vector<PII> vec(n);
        for(int i = 0; i < n; i ++)
        {
            scanf("%lld", &vec[i].x);
            vec[i].y = i;
        }
        sort(vec.begin(), vec.end());
        int left = 1, right = 1;
        LL ans = 0;
        vector<int> res(n);
        for(int i = n - 1; i >= 0; i --)
        {
            if(i % 2)
            {
                ans += 2 * left * vec[i].x;
                res[vec[i].y] = -left;
                left ++;
            }
            else
            {
                ans += 2 * right * vec[i].x;
                res[vec[i].y] = right ++;
            }
        }

        printf("%lld\n", ans);
        printf("%d", 0);
        for(int i = 0; i < n; i ++)
        {
            printf(" %d", res[i]);
        }
        puts("");
    }
    return 0;
}

C. Divan and bitwise operations

题目大意：对于一个序列a， 给出m段下标从l 到r的异或值。求出整个a序列的异或值
位运算、组合数学

感悟

1. 我看到该题没有啥想法，看完题解也只能说是个人的感悟了。
2. 我们没有必要构造出来a序列，可以大胆的猜是不是不用构造。最大的阻碍：不知道第i位有几个1.假设有k个1：对答案的贡献：
   
   
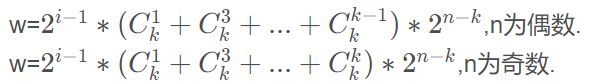
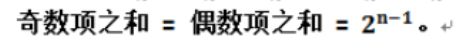
   因此第i位对答案的贡献：
   w = 2^(i - 1) * 2 (n - 1)
   所以：只要有大于等于1个数第i位为1， 对答案的贡献是相同的

#include 
#define x first
#define y second
using namespace std;
typedef long long LL;
typedef pair<LL, int> PII;
const int N = 2e5 + 10, mod = 1e9+7;
int main(void)
{
    int  T;
    scanf("%d", &T);
    vector<LL> vec(N);
    vec[0] = 1;
    for(int i = 1; i < N;i ++)
    {
        vec[i] = (vec[i - 1] * 2ll) % mod;
    }
    while(T --)
    {
        int n, m;
        scanf("%d%d", &n, &m);
        LL ans = 0;
        while(m --)
        {
            int l, r;
            LL x;
            scanf("%d%d%lld", &l, &r, &x);
            ans |= x;
        }
        cout << (ans * vec[n - 1]) % mod << endl;
    }
    return 0;
}

D1. Divan and Kostomuksha (easy version)

题目描述：给出一个数组，可以重新排列数组中的数，使得gcd(a[1], a[2]) + gcd(a[1], a[2], a[3]) + gcd(a[1], a[2], a[3]…a[n]) 最大，求次最大值
贪心、dp、gcd的性质
分析：

1. 这题是 dp, (我也没想到。。。)
   试想a数组若是：2 2 3 6， 我们该怎么排使得答案最优？
   容易想到：6 2 2 3
   即若gcd = x， x的倍数应该排在x的前边。
   若y与x互质，若y放到x序列后边，那么y以及y的倍数对答案的贡献只是1
2. 代码实现：cnt[x]表示x以及x的倍数有多少个。根据dp[x]， 更新x的倍数即dp[tx],
   dp[tx] = max(dp[tx], cnt[tx] * (tx - x) + dp[x]);
   如上述的6 2 2 3，
   dp[1] = cnt[1] = 4, dp[2] = 2 * 3 + 1 = 7, dp[6] = dp[2] + (6 - 2) * 1 = 11
   时间复杂度：n logn。

处理完后，我们求一遍dp[i]的最大值即可。

#include 
#define x first
#define y second
using namespace std;
typedef long long LL;
const int N = 1e5 + 10, M = 5e6 + 10;
int a[N];
LL cnt[M], dp[M];
int main(void)
{
    int n;
    scanf("%d", &n);
    for(int i = 1; i <= n; i ++) scanf("%d", &a[i]), cnt[a[i]] ++;
    for(int i = 1; i < M; i ++)
    {
        for(int j = i + i; j < M; j += i)
        {
            cnt[i] += cnt[j];
        }
    }
    LL ans = 0;
    dp[1] = cnt[1];
    for(int i = 1; i < M; i ++)
    {
        for(int j = i + i; j < M; j += i)
        {
            dp[j] = max(dp[j], dp[i] + cnt[j] * (j - i));
        }
    }
   // cout << dp[1] <<" " <
    for(int i = 1; i < M; i ++)
    {
        ans = max(ans, dp[i]);
    }
    cout << ans <<endl;
    return 0;
}

D2. Divan and Kostomuksha (hard version)

题目大意与D1相同，但数据范围扩大到1e7。
一个优化：我们不全部枚举x的整数倍，而是x的素数倍数。因为若tx不是x的素数倍数，即t不是素数，tx和x之间还可以加别的数。

代码优化

1. cnt数组的处理：输入时对每个数计数。
   cnt数组整体与上题意义一样，但不同点：此题tx为素数倍数，因此枚举素数t， 更新cnt数组。

2. dp数组的含义与上题相同，但因为枚举的素数倍数tx，因此x前必须确定紧跟着哪个素数倍数最优，这便是第二重循环的含义。
   i从大到小枚举，这样最后确定的dp[1],确定了1前跟的最优数， dp[1]就是答案。
   解释temp:算出加入这个素数倍数在x前面，会贡献多少

#include 
#define x first
#define y second
using namespace std;
const int N = 2e7 + 10;
long long cnt[N], dp[N];
long long primes[N];
bool book[N];
int t, n;
int main()
{
    //预处理质数数组
    for(int i = 2; i <= N - 1;i ++)
    {
        if(!book[i])
        {
            primes[t ++] = i;
            for(int j = i * 2; j < N; j += i)
            {
                book[j] = 1;
            }
        }
    }
    scanf("%d", &n);
    int num;
    for(int i = 1; i <= n; i ++) scanf("%d", &num), cnt[num] ++;

    for(int i = 0; i < t; i ++)
    {
        int p = primes[i]; //当前素数，
        for(int j = N / p; j; j --) //枚举每一个数，最大是 N / p
        {
            cnt[j] += cnt[j * p];
        }
    }

    for(int i = N - 1; i; i --){
        long long temp = 0;
        for(int j = 0; j < t && i * primes[j] < N; j ++)
        {
            temp = max(temp, dp[i * primes[j]] - cnt[primes[j] * i] * i);
        }
        dp[i] = temp + cnt[i] * i;
    }
    cout << dp[1] <<endl;
    return 0;
}

昨天是1.12日，晚上累了没写完这篇博客，今天早上重新思考的D2，发现思路仿佛比昨天清晰了。。。坚持下去，cf想上大大大大分，，嘤嘤嘤

这绿油油的一片，给人一种好心情。冲！！！