论文阅读: BI-GCN
paper name:BI-GCN: Boundary-Aware Input-Dependent Graph Convolution Network for Biomedical Image Segmentatation
论文名称:边界感知输入独立的图卷积网络
论文地址: arxiv:2110.14775
代码:未公布
摘要:
分割是图像处理中的重要步骤,而卷积操作是受限于局部感受野的,所以全局信息的提取模型对于分割任务而言意义重大。所以本文就应用图卷积来解决这一问题,并且提出了一个Laplacian方法的改良版。不同于现有的方法,本文提出的Laplace操作是与数据独立的,并且本文引入了两个注意力对角矩阵学习节点之间的关系。具体来说,我们通过学习图表示来对不同类的边界感知区域相关性进行建模和推理,该图表示能够通过沿对象边界的空间增强来操作不同区域的远程语义推理。模型既适合于获取全局语义区域信息,同时也能同时适应局部空间边界特征。
实验证明,模型很有效!
数据集: 视盘视杯分割,息肉数据集。
引言:
在生物医学图像中具有挑战的两个方面:
视盘视杯分割,用于查出青光眼。
结直肠息肉分割,用于查出结肠癌。
二者都是很重要的医学影像分析的对象。并且精确的影像分割处理是非常有意义的。
每年在顶会和顶刊中都有相关方面的工作,比如Pranet[2020] 和 [2019]selective feature aggregation network 使用前景查出机制研究背景和对象之间的相关性,在息肉分割任务中取得了好的结果。对于CNN的局部感受野的限制性,16年提出了密集的膨胀卷积块作为环节问题的方式,18年提出了一个多尺度输入和侧输出机制。这里点出来了卷积神经网络的缺陷,堆叠的局部感受机制并不能处理长期的上下文关系,long range context relationship。这也是一个老生常谈的词语了,其实还是卷积核本身的问题,局部感受。 而在细粒度的语义分割任务中,全局信息的学习仅仅依靠卷积是不够的,并且深度卷积会丢失浅层的信息。并且是无差别的丢失。
问题:用语言来形容就是:一种倾向:局部区域众多的相似像素分为一类,而距离会对哪怕是同一对象的像素之间的关系造成干扰。
而基于图卷积类Laplace平滑的这种信息聚合模式在全局信息推理的应用上提供了思路。
从与数据成独立性的laplace矩阵中初始化图结构。而这种图模型后面也有可以训练的。与先前的处理过程不同的是,本文使用初始化邻接矩阵的方式实现了与输入数据无关的这样一种相似度矩阵。用于评估节点之间的关系。
与图像的模式不同,基于多边形的方式是用来探索对象边界的空间特征,这些方法沿着边界回归了预定义的节点位置,然后将预测的顶点相连从而形成整个对象的边界。 即,使用顶点来包围图像区域。
这里引用的文章有:2020年 ECCV,
Regression of instance boundary by aggregated CNN and GCN。
聚合CNN和GNN,直接回归视盘视杯边界的坐标。(上面有图节点。) 边界在分割任务中的能力是不言而喻的。
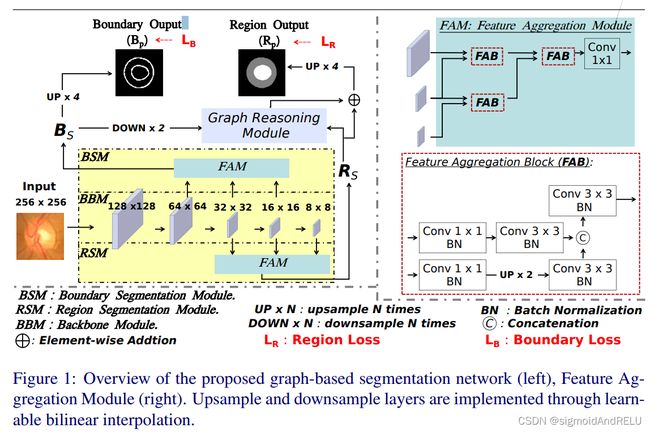
而在医学图像分割,相比较区域像素覆盖,边界精度更能显示出病灶区域的中心和范围。而本文的贡献在此:提出了一种具有边界感知的能力的卷积,明确利用边界信息将边界特征融合到所提出的图卷积中。 在作者2021的TMI中用到的是GCN的思想去处理医学图像的边界信息问题,并且同当前众多文献定义的多任务学习问题。通过骨干学习模型来对输入图像的多层次特征用图节点方式解释不同类的边界感知区域。 在模型中,前层和深层的backbone上分别加上了一个特征聚合模块,来学习便捷和区域特征。这两个模型的名字为BSM, RSM。他们的输出都将成为GRM的输入,这个GRM就是我们看过的图推理模块。这个东东可以用来处理长程关联问题。
详细地说,RSM的区域输出(RS)和BSM的边界输出(BS)被嵌入到图表示中。在GRM中,我们提出了一种新的与边界感知的输入相关的图卷积(BI-GConv)。具体来说,输入相关的邻接矩阵是根据顶点嵌入的输入特征进行细化的估计结果。
Classic Graph Convolution
回顾一下经典的图卷积,给定一张图: G = ( V , E ) G=(V, E) G=(V,E),正则化的:Laplacian 矩阵是 L = I − D − 1 2 A D − 1 2 L = I - D^{\frac{-1}{2}}AD^{\frac{-1}{2}} L=I−D2−1AD2−1, I是单位矩阵。A是邻接矩阵,D为度数矩阵,例如 D i i = ∑ j A i , j D_{ii}=\sum_jA_{i,j} Dii=∑jAi,j. 图的laplacian 是一个半正定对称矩阵,所以根据线性代数的知识,它可以被分解为傅里叶变化的基, L = U Λ U T L = UΛU^T L=UΛUT。所以普方法中,i和j定义为 傅里叶空间 i ∗ j = U ( ( U T i ) . ( U T j ) ) i * j = U((U^Ti).(U^Tj)) i∗j=U((UTi).(UTj))。 U的列是正交特征向量, U = [ u 1 , … … , U n ] U=[u_1, ……,U_n] U=[u1,……,Un], Λ = d i a g ( [ λ 1 , … … , λ n ] ) Λ=diag([λ_1,……,λ_n]) Λ=diag([λ1,……,λn]), 是非负特征值。因为U不稀疏,计算量大,所以在2017年,defferrard 等人,提出了一个在图上的卷积策略,通过使用普方法的滤波器来实现,而这个卷积核使用的是傅里叶空间中的递归切比雪夫多项式。滤波器gθ 是切比雪夫多项式k阶展开式的参数,如 g θ = ∑ k θ k T k ( L ^ ) gθ = \sum_kθ_kT_k(\hat{L}) gθ=∑kθkTk(L^),其中θ是切比雪夫系数的向量。 L ^ = 2 L λ m a x − I N \hat{L} = \frac{2L}{λ_{max} }- I_N L^=λmax2L−IN是重构的Laplacian矩阵, T k T_k Tk是切比雪夫k阶多项式。
对应的laplace矩阵是手动设置的。所以经典的图卷积是独立于输出的图卷积。
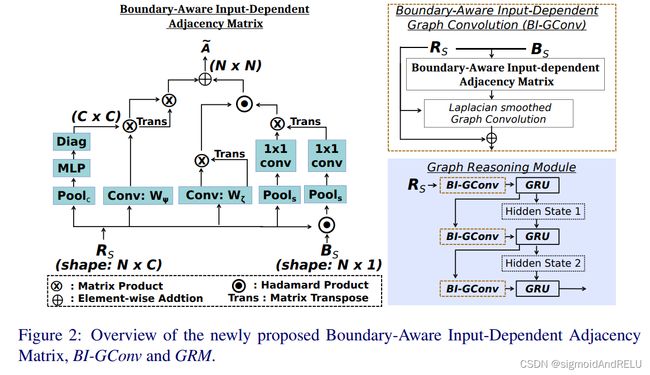
Boundary-Aware Input-dependent Graph Convlution BI-GConv
到这里,是本文的中心思想部分:
考虑到输入特征 R s ∈ R N × C R_s ∈ R^{N×C} Rs∈RN×C,N是输入特征的空间点的数量,C是通道大小。首先,我们创建了独立于输入的邻接矩阵,这一步可以分解为下列步骤:
将两个对角矩阵作为执行通道注意力的工具,而这个通道注意力是针对输入节点的点积距离产生的,同时测量空间注意力权重,衡量不同节点之间的关系。
例如:
Λ ^ C ( R s ) ∈ R C × C \hat{Λ}^C(R_s) ∈R^{C×C} Λ^C(Rs)∈RC×C是一个对角矩阵,就是通道注意力的点积距离。
Λ ^ s ( R s ) ∈ R N × N \hat{Λ}^s(R_s) ∈R^{N×N} Λ^s(Rs)∈RN×N是一个对角矩阵,就是衡量不同节点之间的空间权重关系。
其中: Λ ^ C ( R s ) = d i a g ( M L P ( P o o l c ( R s ) ) ) \hat{Λ}^C(R_s) = diag(MLP(Pool_c(R_s))) Λ^C(Rs)=diag(MLP(Poolc(Rs)))
这个比较好理解,毕竟老通道注意力了。Pool指的是每一个节点嵌入作最大池化。
Λ ^ S ( R s ) = d i a g ( C o n v ( P o o l c ( R s ) ) ) \hat{Λ}^S(R_s) = diag(Conv(Pool_c(R_s))) Λ^S(Rs)=diag(Conv(Poolc(Rs)))
这个就得看看,pool还是最大池化,但是它是对一个通道维度上的节点的每个位置作操作,其实跟普通的空间注意力差不多。
Conv指的是1*1的卷积。
所以通过公式我们就可以得到一个数据相关的邻接矩阵。 A ‾ = ψ ( R s , W ψ ) . Λ ^ c ( R s ) ⋅ ψ ( R s , W ψ ) T + φ ( R s , W φ ) ⋅ φ ( R s , W φ ) T h ( ⋅ ) Λ ^ s ( R s ) \overline{A} = ψ(R_s, W_ψ) . \hat{Λ}^c(R_s)·{ψ(R_s, W_ψ)}^T +φ(R_s,W_φ)·{φ(R_s, W_φ )}^T h(·)\hat{Λ}^s(R_s) A=ψ(Rs,Wψ).Λ^c(Rs)⋅ψ(Rs,Wψ)T+φ(Rs,Wφ)⋅φ(Rs,Wφ)Th(⋅)Λ^s(Rs)
定睛一看, ψ ψ ψ和 φ φ φ都是1*1的卷积,而前者作的是正常矩阵乘法,后者却涉及到hadamard 乘法,即点乘,要是用torch.einsum()公式如下所示:
import torch
a=torch.arange(24).view(2, 3, 4)
b=torch.ones_like(a) * 2
bmul = torch.einsum('ijk,ijk->ijk',[a,b])
print(bmul)
附上原文
文中多次用到embedding这个词,这里有一个相关博客,看哭了。
后来想想,就是一个数据的转换问题,前有图结构映射到隐藏空间,然后再映射回来,中间的隐藏空间中有卷积的操作,而这也是一个空间的节点嵌入问题,异曲同工。当然,本文用的是1*1的卷积来完成此操作。而W是可训练权重。
第二步:如何将输入信息同这两个操作结合呢?
下式:
Λ ^ b s ( R s , B s ) = C o n v ( P o o l s ( R s ) ) ∗ C o n v ( P o o l s ( h p ( R s , B s ) ) T \hat{Λ}^s_b(R_s, B_s) = Conv(Pool_s(R_s)) * {Conv(Pool_s(hp(R_s , B_s))}^T Λ^bs(Rs,Bs)=Conv(Pools(Rs))∗Conv(Pools(hp(Rs,Bs))T
B_s 是N1维的输入,进入Laplace矩阵中,这样能够让我们平滑对象边界的隐藏空间,即,将它同空间权重矩阵相乘,然后得到为我们的边界感知空间权重矩阵。hadamard product 在通道方向上广播。这样,边界上的像素就被赋予了更大的权重。由此,结合了边界感知的图卷积能够在推理不同区域的相关性时考虑边界的空间特征,就是给图的区域相关性提供参考。而这样的假设能够求得输入的邻接矩阵:
A ~ = ψ ( R s , W ψ ) . Λ ~ c ( R s ) ⋅ ψ ( R s , W ψ ) T + ζ ( R s , W ζ ) ⋅ ζ ( R s , W ζ ) T h ( ⋅ ) Λ ~ b s ( R s , B s ) \widetilde{A} = ψ(R_s, W_ψ) . \widetilde{Λ}^c(R_s)·{ψ(R_s, W_ψ)}^T +ζ(R_s,W_ζ)·{ζ(R_s, W_ζ)}^T h(·)\widetilde{Λ}_b^s(R_s, B_s) A =ψ(Rs,Wψ).Λ c(Rs)⋅ψ(Rs,Wψ)T+ζ(Rs,Wζ)⋅ζ(Rs,Wζ)Th(⋅)Λ bs(Rs,Bs)
W可训练, ζ ∈ N × C ζ∈N×C ζ∈N×C, 由11的卷积实现。在得到A的前提下,正则化的laplace矩阵就给出来了, L ~ = I − D ~ − 1 2 A ~ D ~ − 1 2 \widetilde{L} = I - \widetilde{D}^{-\frac{1}{2}}\widetilde{A}\widetilde{D}^{-\frac{1}{2}} L =I−D −21A D −21, I I I是单位矩阵,D是显示每个节点度数的对角矩阵。 D ~ i i = ∑ j A ~ i , j \widetilde{D}_{ii} = \sum_j \widetilde{A}_{i, j} D ii=∑jA i,j, 为了降低匀速拿的复杂度,令:
D ~ = d i a g ( ψ ( Λ ~ C ( ψ T ⋅ 1 → ) ) + d i a g ( ζ ( ζ T ⋅ 1 → ) ) h ( ⋅ ) Λ ~ b s \widetilde{D} = diag(ψ(\widetildeΛ^C(ψ^T · \overrightarrow 1)) + diag(ζ(ζ^T·\overrightarrow1)) h(·) \widetilde{Λ}_b^s D =diag(ψ(Λ C(ψT⋅1))+diag(ζ(ζT⋅1))h(⋅)Λ bs
其中 1 → \overrightarrow 1 1是全一向量,括号内的式子优先运算,这样改变了计算的次序,整合一下,单一的
BI-Gconv : Y = σ ( L ~ ⋅ R s ⋅ W G ) + R s Y=σ(\widetilde{L}·R_s·W_G)+R_s Y=σ(L ⋅Rs⋅WG)+Rs
这里还是用了残差的思想。σ是ReLu激活函数。
将BI-GConv层嵌入Graph Reasoning Module,由三个BI-GConv变的(Gated Recurrent Unit) GRU相连接,这个图推理模型取得了最好的效果。
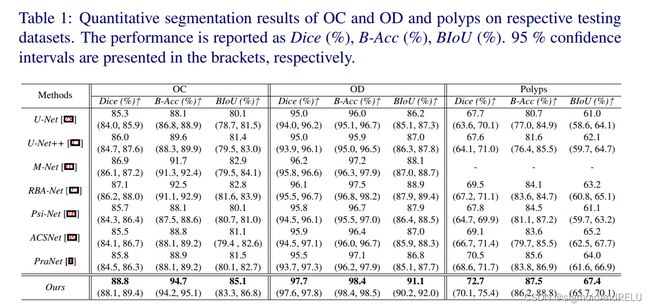
实验就略了,哎,强啊。
要是觉得有帮助,一键三连支持我!!