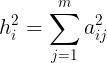因子分析 factor analysis (二 ) ： 因子分析模型

因子分析系列博文: 

因子分析 factor analysis (一 )：模型的理论推导

因子分析 factor analysis (二 ) ： 因子分析模型

因子分析 factor analysis (三) ： 因子载荷矩阵的估计方法

因子分析 factor analysis (四) ： 因子旋转（正交变换）

因子分析 factor analysis (五) ： 因子得分 

因子分析 factor analysis (六) ：用因子分析法进行综合评价

因子分析 factor analysis (七) ：因子分析法与主成分分析的异同

---

目录

一  因子分析的原理           

二   因子分析模型               2.1  数学模型           2.2  因子分析模型的性质 

 2.3  因子载荷矩阵中的几个统计性质 

---

一  因子分析的原理          

因子分析(factor analysis)是一种数据简化的技术。它通过研究众多变量之间的内部依赖关系，探求观测数据中的基本结构，并用少数几个假想变量来表示其基本的数据结构。这几个假想变量能够反映原来众多变量的主要信息。原始的变量是可观测的显 在变量，而假想变量是不可观测的潜在变量，称为因子。

因子分析与回归分析不同，因子分析中的因子是一个比较抽象的概念，而回归因子有非常明确的实际意义。

主成分分析分析与因子分析也有不同，主成分分析仅仅是变量变换，而因子分析需要构造因子模型。

主成分分析:原始变量的线性组合表示新的综合变量，即主成分。

因子分析：潜在的假想变量和随机影响变量的线性组合表示原始变量。 

二   因子分析模型 

 2.1  数学模型    

 

2.2  因子分析模型的性质 

（1）原始变量 X 的协方差矩阵的分解 

 （2）载荷矩阵不是唯一的

 设 T 为一个  的正交矩阵，令   ,则模型可以表示为  

 

2.3  因子载荷矩阵中的几个统计性质 

2.3.1 因子载荷 的统计意义

因子载荷 是第   个变量与第 个公共因子的相关系数，反映了第i个变量与第 j
个公共因子的相关重要性。绝对值越大，相关的密切程度越高。

2.3.2  变量共同度的统计意义  

变量 的共同度是因子载荷矩阵的第i行的元素的平方和，记为      

对（49）式两边求方差，得

可以看出所有的公共因子和特殊因子对变量  的贡献为1。如果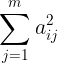 非常靠近1，非常小，则因子分析的效果好，从原变量空间到公共因子空间的转化效果好。

2.3.3 公共因子 方差贡献的统计意义

因子载荷矩阵中各列元素的平方和     称为    对所有的的方差贡献和，衡量的相对重要性。

---

因子分析系列博文: 

因子分析 factor analysis (一 )：模型的理论推导

因子分析 factor analysis (二 ) ： 因子分析模型

因子分析 factor analysis (三) ： 因子载荷矩阵的估计方法

因子分析 factor analysis (四) ： 因子旋转（正交变换）

因子分析 factor analysis (五) ： 因子得分

因子分析 factor analysis (六) ：用因子分析法进行综合评价

因子分析 factor analysis (七) ：因子分析法与主成分分析的异同