2021年辽宁省大学生数学建模
2021年辽宁省大学生数学建模
C题 碳中和问题
碳中和是指人为排放量(化石燃料利用和土地利用)被人为努力(木材蓄积量、土壤有机碳、工程封存等)和自然过程(海洋吸收、侵蚀-沉积过程的碳埋藏等)所吸收。简单来说,就是想办法把原本将会滞留在大气中的二氧化碳减弱或吸收。
请搜集相关数据与信息,完成以下问题:
一、量化分析能源结构与产业结构碳排放的驱动因素与能源消费碳排放的结果因素关系和演化规律,建立相应的数学模型。
二、针对问题一中难以度量的驱动因素和结果因素以及关系属性,对碳排放与吸收的变化规律进行分析。
三、根据上述分析结果,结合不同行业和区域特点,给出碳中和实现的阶段性和全局性建议。
模型的建立与求解:
将碳排放变动因素分解为经济效应、产业结构变动效应、能源利用效率因素和能源消费结构变动效应,建立基于经济效应、产业结构变动效应、能源利用效率因素和能源消费结构变动效应的指数分解模型:

其中,i表示产业类别,j表示能源消费种类;C表示碳排放总量,Cij表示i产业消耗j种能源的碳排放量;Q表示经济总量,Qi表示i产业增加值;E、Ei、Eij分别表示能源消耗总量、i产业的能源消费总量、i产业对j种能源的消费量;Si表示i产业增加值所占比重;Ii表示i产业能源消费强度;Mij表示j种能源在i产业中占比,Uij表示i产业中消费j种能源的碳排放因子系数。
在式(1)中,我们将碳排放量差异分解为:
![]()
上述分项中分别代表经济总量、产业结构、能源消耗强度、能源结构和碳排放系数的变动对总的排放水平的影响。由此,我们得到了影响碳排放量的关系函数。
为探究影响能源结构与产业结构碳排放的驱动因素与能源消费碳排放的结果因素关系和演化规律,除上述得出的影响能源结构与产业结构碳排放的驱动因素外,我们还需得出产业结构、能源结构的变动与能源消费碳排放之间的关系,最终由近几年的能源结构、产业结构变动的数据结合能源消费数据,建立关于能源消费碳排放的数学预测模型,得出演化规律。
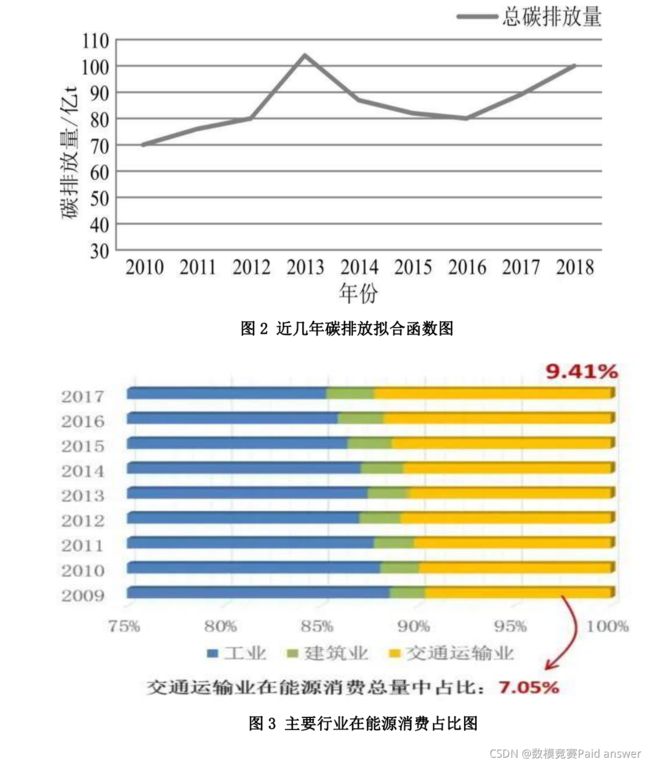
由采集到的数据及相关资料,我们使用拉格朗日插值拟合的方法对近几年的碳排放及产业结构、能源结构数据进行分析。
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
def GM11(x, n):
'''灰色预测
x:序列,numpy 对象
n:需要往后预测的个数
''' x1 = x.cumsum() # 一次累加
z1 = (x1[:len(x1) - 1] + x1[1:]) / 2.0 # 紧邻均值
z1 = z1.reshape((len(z1), 1))
B = np.append(-z1, np.ones_like(z1), axis=1)
Y = x[1:].reshape((len(x) - 1, 1))
# a 为发展系数 b 为灰色作用量
[[a], [b]] = np.dot(np.dot(np.linalg.inv(np.dot(B.T, B)), B.T), Y) # 计算参数
result = (x[0] - b / a) * np.exp(-a * (n - 1)) - (x[0] - b / a) *
np.exp(-a * (n - 2))
S1_2 = x.var() # 原序列方差
e = list() # 残差序列
for index in range(1, x.shape[0] + 1):
predict = (x[0] - b / a) * np.exp(-a * (index - 1)) - (x[0] - b / a) * np.exp(-a * (index - 2))
e.append(x[index - 1] - predict)
S2_2 = np.array(e).var() # 残差方差
C = S2_2 / S1_2 # 后验差比
if C <= 0.35:
assess = '后验差比<=0.35,模型精度等级为好' elif C <= 0.5:
assess = '后验差比<=0.5,模型精度等级为合格' elif C <= 0.65:
assess = '后验差比<=0.65,模型精度等级为勉强' else:
assess = '后验差比>0.65,模型精度等级为不合格' # 预测数据
predict = list()
for index in range(x.shape[0] + 1, x.shape[0] + n + 1):
predict.append((x[0] - b / a) * np.exp(-a * (index - 1)) - (x[0] - b / a) * np.exp(-a * (index - 2)))
predict = np.array(predict)
return {
'a': {'value': a, 'desc': '发展系数'},
'b': {'value': b, 'desc': '灰色作用量'},
'predict': {'value': result, 'desc': '第%d 个预测值' % n},
'C': {'value': C, 'desc': assess},
'predict': {'value': predict, 'desc': '往后预测%d 个的序列' %
(n)}, }
if __name__ == "__main__":
data = np.array([1.2, 2.2, 3.1, 4.5, 5.6, 6.7, 7.1, 8.2, 9.6, 10.6, 11, 12.4, 13.5, 14.7, 15.2])
x = data[0:10] # 输入数据
y = data[10:] # 需要预测的数据
result = GM11(x, len(y))
predict = result['predict']['value']
predict = np.round(predict, 1)
print('真实值:', y)
print('预测值:', predict)
print(result)