FHEW 和 TFHE 的统一框架:标准化 FHE
参考文献:
- [GHS12] Gentry C, Halevi S, Smart N P. Better bootstrapping in fully homomorphic encryption[C]//International Workshop on Public Key Cryptography. Berlin, Heidelberg: Springer Berlin Heidelberg, 2012: 1-16.
- [GHPS12] Gentry C, Halevi S, Peikert C, et al. Field switching in BGV-style homomorphic encryption[J]. Journal of Computer Security, 2013, 21(5): 663-684.
- [AP13] Alperin-Sheriff J, Peikert C. Practical bootstrap** in quasilinear time[C]//Annual Cryptology Conference. Berlin, Heidelberg: Springer Berlin Heidelberg, 2013: 1-20.
- [BV14] Brakerski Z, Vaikuntanathan V. Lattice-based FHE as secure as PKE[C]//Proceedings of the 5th conference on Innovations in theoretical computer science. 2014: 1-12.
- [AP14] J. Alperin-Sheriff and C. Peikert. Faster bootstrapping with polynomial error. In CRYPTO 2014, volume 8616 of Lecture Notes in Computer Science, pages 297–314, 2014.
- [DM15] L. Ducas and D. Micciancio. FHEW: bootstrapping homomorphic encryption in less than a second. In EUROCRYPT (1), volume 9056 of Lecture Notes in Computer Science, pages 617–640. Springer, 2015.
- [GINX16] N. Gama, M. Izabach`ene, P. Q. Nguyen, and X. Xie. Structural lattice reduction: Generalized worst-case to average-case reductions and homomorphic cryptosystems. In EUROCRYPT 2016, volume 9666 of Lecture Notes in Computer Science, pages 528–558, 2016.
- [CGGI16] I. Chillotti, N. Gama, M. Georgieva, and M. Izabach`ene. Faster fully homomorphic encryption: Bootstrapping in less than 0.1 seconds. In ASIACRYPT (1), volume 10031 of Lecture Notes in Computer Science, pages 3–33, 2016.
- [ACC+18] M. Albrecht, M. Chase, H. Chen, and et al. Homomorphic encryption security standard. Technical report, HomomorphicEncryption.org, Toronto, Canada, November 2018.
- [Mic18] D. Micciancio. On the hardness of learning with errors with binary secrets. Theory Comput., 14(1):1–17, 2018.
- [Mic19] D. Micciancio. Fully homomorphic encryption from the ground up. Invited Talk, Eurocrypt 2019, 2019.
- [EJK20] T. Espitau, A. Joux, and N. Kharchenko. On a hybrid approach to solve binary-lwe. Cryptology ePrint Archive, Report 2020/515, 2020.
- [MP21] Micciancio D, Polyakov Y. Bootstrapping in FHEW-like cryptosystems[C]//Proceedings of the 9th on Workshop on Encrypted Computing & Applied Homomorphic Cryptography. 2021: 17-28.
- 全同态加密:FHEW
- 全同态加密:TFHE
- 环面上 FHE 的快速自举:GSIS/SLWE
- TFHE 的全同态模结构(FHE Module Structure)
- Linear Decryption: Rate-1 FHE & TLP
- Branching Program(5-PBP)
文章目录
- Unified Framework
-
- Background
- RLWE Encryption
- Bootstrapping
-
- Rounding & Gates
- AP/TFHE
- GINX/TFHE
- Comparison
-
- Runtime
- Size of BK
- Recommendation
Unified Framework
Background
[MP21] 比较了 [MD15] 的原始 FHEW 和 [GCCI16] 的原始 TFHE 的异同,然后将它们实现在了一个统一的框架内。
第二代 FHE 方案(包括 BGV/BFV/CKKS)的自举速度很慢:因为 BGV-like 支持的同态运算是算术的,而自举中需要的模约减、园整都是布尔的。[GHS12] 提出使用特殊的底层模数 q = 2 l q=2^l q=2l,从而根据 ( 2 a + b ) 2 ( m o d 4 ) = b 2 = b (2a+b)^2 \pmod4=b^2=b (2a+b)2(mod4)=b2=b 可以的不断消除的低位比特,因此可以在完全的算术电路下执行自举算法。[GHS12] 还利用 “p-adic integers”(p进数)和 ““Hensel Lifting” 把 [SV11] 的 SIMD 扩展到了槽 Z 2 l \mathbb Z_{2^l} Z2l(而非 G F ( 2 l ) GF(2^l) GF(2l)),于是可以并行执行模约减和舍入任务,从而实现 BGV 的非布尔电路的自举。[AP13] 则使用素数 p p p 在 tower of cyclotomic rings 上的连续分解,以及 [GHPS12] 的 Field switching 技术,进一步改进了 BGV 的自举。但是,它们的扩展 SIMD 的代数结构特别复杂,实现困难(博主我甚至看不懂)。另外,BGV 和 BFV 的自举程序要求格上困难问题的近似因子是超多项式的(grow superpolynomially in the lattice dimension n),这个假设太强了。
第三代 FHE 方案(包括 GSW/FHEW/TFHE)的自举速度就比较快,并且自举的安全性假设也更弱:GSW 本身是由若干个独立的 LWE/BGV/GFV 密文拼接出来的,因此安全性基于 standard LWE 假设。[BV14] 展示了 GSW 的非对称噪声增长,利用连续的 Dimension-Modulus Reduction,给出了第一个 “量子归约到近似因子为 O ~ ( n 1.5 + ϵ ) \tilde O(n^{1.5+\epsilon}) O~(n1.5+ϵ) 的 GapSVP 问题” 以及 “经典归约到近似因子为 O ~ ( n 2 + ϵ ) \tilde O(n^{2+\epsilon}) O~(n2+ϵ) 的 GapSVP 问题” 的全同态加密方案(换句话说,自举程序并不会降低 FHE 的安全性,因此 FHE 和一般的 PKE 同样安全),其近似因子仅为多项式的。但它使用 GSW 执行 5-PBP 形式的布尔自举程序,速度依然较慢。[AP14] 和 [GINX16] 都利用了解密函数的特殊性:AP 把内积运算转化为 subset-sum,把解码运算转化为 equality test,使用对称群的算术电路实现自举;而 GINX 将解密函数表示为宽度有限的 OBDD 图,使用 MUX-based LUT 来实现自举。之后的 FHEW 提出采取同态累加器以及查表操作实现 AP 策略,速度大幅提高;而 TFHE 则利用这种累加器实现 GINX 策略,自举秘钥的规模大大减小。FHEW 和 TFHE 基于的困难假设也只需要多项式增长的近似因子,自举足够安全。
AP/FHEW 和 GINX/TFHE 的不同之处:
- 自举算法(这是最大的不同)
- FHEW 采取了 [AP14] 的自举策略:对密文做二进制分解,同态解密时利用各个比特挑选对应的自举秘钥,计算出累加值之后提取出自举结果
- TFHE 采取了 [GINX16] 的自举策略:限制私钥是二元分布,同态解密时利用各个比特执行同态的 MUX 门,计算出累加值之后提取出自举结果
- 秘密分布(依赖于自举算法)
- FHEW 的私钥分布不收限制,可以是:二元、三元、高斯、均匀
- TFHE 的私钥分布受限,必须是二元取值的
- 安全性假设(TFHE 的假设更强)
- FHEW 依赖于 standard LWE/RLWE 假设,以及 circular secure 假设
- TFHE 依赖于 LWE/RLWE over Torus with Binary secret distribution 假设,以及 circular secure 假设
- 优化技术(这是通用的)
- FHEW 使用 Add 实现 NAND 门(LWE 方案的乘法)
- TFHE 使用 FHE Module Structure 实现乘法门(ACC 方案的乘法)
不过 FHEW 和 TFHE 本质上仅仅是同态累加器的实现不同,因此 [MP21] 将两者统一,使得它们满足 [ACC+18] 的全同态加密标准化建议:密文框架采用 FHEW 的密文格式(LWE/RLWE/RGSW),自举框架采用 FHEW 的累加器抽象,优化技术采用 TFHE 的外积运算。[MP21] 采取了更多的优化技术,包括:对 FHEW 的时间/空间权衡(更大的进制分解)、对 TFHE 的私钥分布扩展(利用自举例程的线性)。
框架为:
- 消息 μ ∈ Z 4 \mu \in \mathbb Z_4 μ∈Z4 加密在 LWE 密文中,密文的代数结构是 Z q n + 1 \mathbb Z_q^{n+1} Zqn+1,它仅支持同态加法,可以容忍极高的噪声比率 q / 8 q/8 q/8
- 使用 RLWE 密文(自举秘钥是 RGSW 密文)实现同态累加器,代数结构是 Z Q [ x ] / ( x N + 1 ) \mathbb Z_Q[x]/(x^N+1) ZQ[x]/(xN+1),要求 q ∣ 2 N q|2N q∣2N 使得这个分圆环包含 q q q 阶循环子群 ⟨ x 2 N / q ⟩ \langle x^{2N/q}\rangle ⟨x2N/q⟩
- 基于 AP 或者 GINX 策略,实现 FHEW 和 TFHE 的两种累加器
- 自举程序的输入是 LWE 密文,使用累加器计算出内积,然后查表提取出解密结果(此时的密文代数结构 Z Q N + 1 \mathbb Z_Q^{N+1} ZQN+1),最后执行秘钥-维度-模数切换
RLWE Encryption
分园环 R = Z [ x ] / ( x N + 1 ) R=\mathbb Z[x]/(x^N+1) R=Z[x]/(xN+1),RLWE 密文模数 Q ∈ Z Q \in \mathbb Z Q∈Z,密文代数结构 R Q = R / Q R R_Q=R/QR RQ=R/QR
私钥 s ∈ R s \in R s∈R,明文 m ∈ R Q m \in R_Q m∈RQ,随机带 a ← R Q a \gets R_Q a←RQ,离散高斯噪声 e ← χ σ e \gets \chi_\sigma e←χσ(根据 [ACC+18] 的标准化建议,实用 σ ≈ 3.2 \sigma\approx 3.2 σ≈3.2,理论 σ = N \sigma=\sqrt N σ=N),那么对称加密:
R L W E s ( m ) = ( a , a s + e + m ) ∈ R Q 2 RLWE_s(m) = (a, as+e+m) \in R_Q^2 RLWEs(m)=(a,as+e+m)∈RQ2
解密运算
R L W E s − 1 ( a , b ) = b − a s = m + e ∈ R Q RLWE_s^{-1}(a,b) = b-as=m+e \in R_Q RLWEs−1(a,b)=b−as=m+e∈RQ
噪声项 E r r ( ( a , b ) ; m ) = b − a s − m = e ∈ R Q Err((a,b);m)=b-as-m=e \in R_Q Err((a,b);m)=b−as−m=e∈RQ
根据 [Mic19],弱线性同态的对称加密,可以扩展为线性同态的对称/公钥加密:对常数做 radix- B g B_g Bg 分解(共 d g = log B g Q d_g=\log_{Bg}Q dg=logBgQ 比特),对明文做 power of B g B_g Bg 预处理,
R L W E s ′ ( m ) = ( R L W E s ( m ) , R L W E s ( B g m ) , ⋯ , R L W E s ( B g d g − 1 m ) ) RLWE_s'(m) = (RLWE_s(m),RLWE_s(B_gm),\cdots,RLWE_s(B_g^{d_g-1}m)) RLWEs′(m)=(RLWEs(m),RLWEs(Bgm),⋯,RLWEs(Bgdg−1m))
这实际上就是 Gadget Matrix,它本身就有一定的纠错能力,因此不需要再用 scaling 纠错。给定常数 r ∈ R Q r \in R_Q r∈RQ,分解为 ∑ i r i B g i \sum_i r_i B_g^i ∑iriBgi,那么定义 ⊙ : R × R L W E ′ → R L W E \odot:R \times RLWE' \to RLWE ⊙:R×RLWE′→RLWE 运算,
r ⊙ R L W E s ′ ( m ) : = ∑ i r i ⋅ R L W E s ( B g i m ) = R L W E s ( ∑ i r i B g i ⋅ m ) r \odot RLWE_s'(m) := \sum_i r_i \cdot RLWE_s(B_g^im) = RLWE_s(\sum_i r_iB_g^i \cdot m) r⊙RLWEs′(m):=i∑ri⋅RLWEs(Bgim)=RLWEs(i∑riBgi⋅m)
最坏情况下,同态数乘导致的噪声增长是 d g ⋅ log B g Q d_g \cdot \log_{B_g} Q dg⋅logBgQ 因子。容易扩展到 ⊙ ′ : R × R L W E ′ → R L W E ′ \odot':R \times RLWE' \to RLWE' ⊙′:R×RLWE′→RLWE′ 运算,
r ⊙ ′ C : = ( r ⊙ C , B g r ⊙ C , ⋯ , B g d g − 1 r ⊙ C ) r \odot' C := (r \odot C,B_gr \odot C,\cdots,B_g^{d_g-1}r \odot C) r⊙′C:=(r⊙C,Bgr⊙C,⋯,Bgdg−1r⊙C)
于是 R L W E ′ RLWE' RLWE′ 就是运算 ⊙ ′ \odot' ⊙′ 下的线性同态的对称加密方案。[Mic19] 指出,线性解密函数可以在线性同态下执行:我们用 R L W E ′ RLWE' RLWE′ 加密 ( − s , 1 ) ⋅ m (-s,1)\cdot m (−s,1)⋅m 的两个分量,
R G S W s ( m ) : = ( R L W E s ′ ( − s ⋅ m ) , R L W E s ′ ( m ) ) RGSW_s(m) := (RLWE_s'(-s \cdot m), RLWE_s'(m)) RGSWs(m):=(RLWEs′(−s⋅m),RLWEs′(m))
这恰好等价于 RGSW 密文: ( − 1 , 0 ) (-1,0) (−1,0) 是 s s s 的无噪声密文, ( 0 , m ) (0,m) (0,m) 是 m m m 的无噪声密文,于是
R L W E s ′ ( − s ⋅ m ) = R L W E s ′ ( 0 ) + ( m , 0 ) d g R L W E s ′ ( m ) = R L W E s ′ ( 0 ) + ( 0 , m ) d g \begin{aligned} RLWE_s'(-s \cdot m) &= RLWE_s'(0) + (m,0)^{d_g}\\ RLWE_s'(m) &= RLWE_s'(0) + (0,m)^{d_g}\\ \end{aligned} RLWEs′(−s⋅m)RLWEs′(m)=RLWEs′(0)+(m,0)dg=RLWEs′(0)+(0,m)dg
对比 [AP14] 给出的 GSW 对称变体,采取 Gadget 矩阵 G = I ⊗ ( 1 , B g , ⋯ , B g d g − 1 ) G=I \otimes (1,B_g,\cdots,B_g^{d_g-1}) G=I⊗(1,Bg,⋯,Bgdg−1),容易发现它们是完全一样的密文。
给定 ( a , b ) = R L W E s ( m 0 ; e 0 ) (a,b) = RLWE_s(m_0;e_0) (a,b)=RLWEs(m0;e0) 和 ( c , c ′ ) = R G S W s ( m 1 ; ( e 1 , e 1 ′ ) ) (c,c')=RGSW_s(m_1;(e_1,e_1')) (c,c′)=RGSWs(m1;(e1,e1′)),我们定义外积 ∘ : R L W E × R G S W → R L W E \circ: RLWE \times RGSW \to RLWE ∘:RLWE×RGSW→RLWE,
( a , b ) ∘ ( c , c ′ ) : = a ⊙ c + b ⊙ c ′ = R L W E s ( ( m 0 + e 0 ) ⋅ m 1 ) (a,b) \circ (c,c') := a \odot c + b \odot c' = RLWE_s((m_0+e_0) \cdot m_1) (a,b)∘(c,c′):=a⊙c+b⊙c′=RLWEs((m0+e0)⋅m1)
这里的 m 1 e 0 m_1e_0 m1e0 是额外的噪声项(另外还有 ( e 1 + e 1 ′ ) ⋅ B g log B g Q (e_1+e_1') \cdot B_g\log_{B_g}Q (e1+e1′)⋅BglogBgQ 的隐藏噪声项)。一般我们选取 RGSW 明文是一个范数极小的环元素,通常是 m 1 = ± x v m_1=\pm x^v m1=±xv,导致产生的偏差 ∥ m 1 e 0 ∥ = ∥ e 0 ∥ \|m_1e_0\|=\|e_0\| ∥m1e0∥=∥e0∥ 很小。
容易把它扩展为 ∘ ′ : R L W E ′ × R G S W → R L W E ′ \circ': RLWE' \times RGSW \to RLWE' ∘′:RLWE′×RGSW→RLWE′,
( c 0 , ⋯ , c d g − 1 ) ∘ ′ C : = ( c 0 ∘ C , ⋯ , c d g − 1 ∘ C ) (c_0,\cdots,c_{d_g-1}) \circ' C := (c_0\circ C,\cdots,c_{d_g-1}\circ C) (c0,⋯,cdg−1)∘′C:=(c0∘C,⋯,cdg−1∘C)
继续扩展为内积 ∘ ′ ′ : R G S W × R G S W → R G S W \circ'': RGSW \times RGSW \to RGSW ∘′′:RGSW×RGSW→RGSW,
( c , c ′ ) ∘ ′ ′ C : = ( c ∘ ′ C , c ′ ∘ ′ C ) (c,c') \circ'' C := (c \circ' C, c' \circ' C) (c,c′)∘′′C:=(c∘′C,c′∘′C)
当我们只需要 RLWE 密文时,只需要最简单的外积 ∘ \circ ∘ 即可,这比计算 RGSW 内积 ∘ ′ ′ \circ'' ∘′′ 的计算复杂度低得多(降低了 2 d g 2d_g 2dg 因子)
Bootstrapping
回顾下,
- LWE 方案:私钥 s ∈ Z n s \in \mathbb Z^n s∈Zn,密文模数 q q q,密文的代数结构是 Z q n + 1 \mathbb Z_q^{n+1} Zqn+1,平凡明文的代数结构是 Z q \mathbb Z_q Zq,考虑纠错码的明文代数结构是 Z t \mathbb Z_t Zt,一般采用形如 q / t ⋅ μ ∈ Z q q/t \cdot\mu \in \mathbb Z_q q/t⋅μ∈Zq 的编码格式
- RLWE 方案:私钥 k ∈ R = Z [ x ] / ( x N + 1 ) k \in R=\mathbb Z[x]/(x^N+1) k∈R=Z[x]/(xN+1),密文模数 Q Q Q,密文的代数结构是 R Q 2 R_Q^2 RQ2,平凡明文的代数结构是 R Q R_Q RQ,不考虑纠错码
- 需要满足 q ∣ 2 N q|2N q∣2N,从而存在 q q q 阶循环子群 ⟨ x 2 N / q ⟩ ⊆ R Q \langle x^{2N/q}\rangle \subseteq R_Q ⟨x2N/q⟩⊆RQ
- 需要满足 Q ≫ q Q\gg q Q≫q,从而使得自举结果的噪声比率足够低
对 LWE 密文 ( a , b ) (a,b) (a,b) 自举时,
- 首先同态计算线性函数 v = b − ⟨ a , s ⟩ v=b-\langle a,s\rangle v=b−⟨a,s⟩,它是消息 μ ∈ Z t \mu \in \mathbb Z_t μ∈Zt 的带噪纠错码字
- 然后同态地查表得到 f ( v ) f(v) f(v) 的值,这里的 f : Z q → Z Q f: \mathbb Z_q \to \mathbb Z_Q f:Zq→ZQ 是反循环函数,满足 f ( v + q / 2 ) = − f ( v ) f(v+q/2)=-f(v) f(v+q/2)=−f(v)
- 最后整理 f ( v ) ∈ Z Q f(v) \in \mathbb Z_Q f(v)∈ZQ,得到 q / t ⋅ μ ∈ Z q q/t \cdot\mu \in \mathbb Z_q q/t⋅μ∈Zq
FHEW 利用基于 RGSW 构造的同态累加器实现上述三个步骤,TFHE 使用 RGSW 和 RLWE 外积加速了同态累加器的实现。[MP21] 进一步采取了两种优化手段:
- 如果函数 f f f 是公开的,我们将常数 b b b 直接反序存储到多项式中,形如 ∑ i f ( b − i ) ⋅ x i \sum_i f(b-i) \cdot x^i ∑if(b−i)⋅xi,这使得提取 f ( v ) f(v) f(v) 更加方便
- 如果自举结果仅是 LWE 密文,那么累加器的状态值只需要是单个 RLWE 密文,而非 RGSW 密文(含 2 d g 2d_g 2dg 个 RLWE 密文)
[MP21] 的同态累加器构造如下:
-
Initialize 阶段,简记为 A C C f ← v ACC_f \gets v ACCf←v
-
公开的反循环函数 f : Z q → Z Q f: \mathbb Z_q \to \mathbb Z_Q f:Zq→ZQ,常数值 v ∈ Z q v \in \mathbb Z_q v∈Zq
-
构造 Lookup Table 为多项式,简记 X = x 2 N / q X=x^{2N/q} X=x2N/q 是 q q q 阶循环子群的生成元,
m ( x ) : = ∑ i = 0 q / 2 − 1 f ( v − i ) ⋅ X i ∈ R Q m(x) := \sum_{i=0}^{q/2-1} f(v-i) \cdot X^{i} \in R_Q m(x):=i=0∑q/2−1f(v−i)⋅Xi∈RQ -
状态是无噪声 RLWE 密文, A C C f : = R L W E k ( m ) = ( 0 , m ) ∈ R Q 2 ACC_f:=RLWE_k(m)=(0,m) \in R_Q^2 ACCf:=RLWEk(m)=(0,m)∈RQ2
-
-
Update 阶段,简记为 A C C f ← + c ⋅ E ( s ) ACC_f \overset{+}{\gets} c \cdot E(s) ACCf←+c⋅E(s)
-
秘密值 s ∈ Z q s \in \mathbb Z_q s∈Zq 的加密 E ( s ) E(s) E(s)(根据 AP 策略、GINX 策略,对应的实现也不同),常数 c ∈ Z q c \in \mathbb Z_q c∈Zq
-
符号 c ⋅ E ( s ) c \cdot E(s) c⋅E(s) 代表同态数乘/盲旋转(也依赖于策略),计算出
R L W E k ( m ⋅ X c ⋅ s ( m o d q ) ) RLWE_k(m \cdot X^{c\cdot s \pmod q}) RLWEk(m⋅Xc⋅s(modq))
-
-
Extract 阶段,简记为 f ( A C C f ) f(ACC_f) f(ACCf)
-
现在累加器的状态为
R L W E k ( m ⋅ X ∑ c ⋅ s ( m o d q ) ) = ( a , b ) ∈ R Q 2 RLWE_k(m \cdot X^{\sum c\cdot s \pmod q}) = (a,b) \in R_Q^2 RLWEk(m⋅X∑c⋅s(modq))=(a,b)∈RQ2 -
我们提取出明文多项式的常数项,
L W E z ( f ( v − ∑ c ⋅ s ) ) = ( a , b 0 ) ∈ Z Q N + 1 LWE_z(f(v-\sum c \cdot s)) = (a,b_0) \in \mathbb Z_Q^{N+1} LWEz(f(v−∑c⋅s))=(a,b0)∈ZQN+1这里 z = ( k 0 , − k N − 1 , ⋯ , − k 1 ) ∈ Z Q N z=(k_0,-k_{N-1},\cdots,-k_1) \in \mathbb Z_Q^N z=(k0,−kN−1,⋯,−k1)∈ZQN 是私钥 k ∈ R Q k \in R_Q k∈RQ 的转置(transpose)。有时人们采取 a ∈ R Q a \in R_Q a∈RQ 的转置,以保持 k k k 原始顺序,这更加自然方便。
-
假设 RLWE 的噪声是 e ( x ) ∈ R Q e(x) \in R_Q e(x)∈RQ,那么 b 0 − ⟨ a , z ⟩ = f ( v − ∑ c ⋅ s ) + e 0 ∈ Z Q b_0-\langle a,z\rangle = f(v-\sum c \cdot s)+e_0 \in \mathbb Z_Q b0−⟨a,z⟩=f(v−∑c⋅s)+e0∈ZQ,做一些后处理得到 L W E s ( μ ∈ Z t ) = ( a ′ , b ′ ) ∈ Z q n + 1 LWE_s(\mu \in \mathbb Z_t)=(a',b') \in \mathbb Z_q^{n+1} LWEs(μ∈Zt)=(a′,b′)∈Zqn+1
-
下面,我们根据 [AP14] 和 [GINX16] 的自举策略,实例化 FHEW 和 TFHE 的同态累加器。
Rounding & Gates
在自举之前,我们先确定函数 f : Z q → Z Q f:\mathbb Z_q \to \mathbb Z_Q f:Zq→ZQ 的设置。
根据 FHEW 的设计,我们使用 m 1 , m 2 ∈ Z 4 m_1,m_2 \in \mathbb Z_4 m1,m2∈Z4 的算术加法,计算出 m 1 + m 2 ∈ Z 4 m_1+m_2 \in \mathbb Z_4 m1+m2∈Z4,容易验证 L S B ( m 1 + m 2 ) = X O R ( m 1 , m 2 ) ∈ Z 2 LSB(m_1+m_2)=XOR(m_1,m_2) \in \mathbb Z_2 LSB(m1+m2)=XOR(m1,m2)∈Z2 以及 M S B ( m 1 + m 2 ) = A N D ( m 1 , m 2 ) ∈ Z 2 MSB(m_1+m_2)=AND(m_1,m_2) \in \mathbb Z_2 MSB(m1+m2)=AND(m1,m2)∈Z2
假设 L W E s ( q / 4 ⋅ m i ) = ( a i , b i ) LWE_s(q/4 \cdot m_i)=(a_i,b_i) LWEs(q/4⋅mi)=(ai,bi) 的噪声项 ∥ e i ∥ < q / 16 \|e_i\| < q/16 ∥ei∥<q/16,那么 L W E s ( q / 4 ⋅ ( m 1 + m 2 ) ) = ( a 1 + a 2 , b 1 + b 2 ) LWE_s(q/4\cdot(m_1+m_2))=(a_1+a_2,b_1+b_2) LWEs(q/4⋅(m1+m2))=(a1+a2,b1+b2) 的噪声项满足 ∥ e 1 + e 2 ∥ < q / 8 \|e_1+e_2\| < q/8 ∥e1+e2∥<q/8,于是缩放倍率 q / 4 q/4 q/4 的纠错码可以解码出正确的消息。
NAND 门对应的映射 N A N D : Z 4 × Z 4 → Z 4 NAND:\mathbb Z_4 \times \mathbb Z_4 \to \mathbb Z_4 NAND:Z4×Z4→Z4 是
0 ↦ 1 , 1 ↦ 1 , 2 ↦ 0 ( 3 ↦ 0 ) 0\mapsto1,\,\,1\mapsto1,\,\,2\mapsto0\,\,(3\mapsto0) 0↦1,1↦1,2↦0(3↦0)
添加上纠错机制, f ′ : Z q → Z Q f':\mathbb Z_q \to \mathbb Z_Q f′:Zq→ZQ 定义为
{ 0 , q / 4 } + ( − q / 8 , q / 8 ) = ( − q / 8 , 3 q / 8 ) ↦ Q / 4 { 2 q / 4 , 3 q / 4 } + ( − q / 8 , q / 8 ) = ( 3 q / 8 , 7 q / 8 ) ↦ 0 \begin{array}{lclcl} \{0,q/4\} + (-q/8,q/8)&=&(-q/8,3q/8) &\mapsto& Q/4\\ \{2q/4,3q/4\} + (-q/8,q/8)&=&(3q/8,7q/8) &\mapsto& 0\\ \end{array} {0,q/4}+(−q/8,q/8){2q/4,3q/4}+(−q/8,q/8)==(−q/8,3q/8)(3q/8,7q/8)↦↦Q/40
另外,自举程序限制了 f f f 是反循环的, f ( v + q / 2 ) = − f ( v ) f(v+q/2)=-f(v) f(v+q/2)=−f(v),因此我们把 f ′ f' f′ 再环面上旋转 − Q / 8 -Q/8 −Q/8 相位,得到的 f : Z q → Z Q f:\mathbb Z_q \to \mathbb Z_Q f:Zq→ZQ 定义为
( − q / 8 , 3 q / 8 ) ↦ Q / 8 ( 3 q / 8 , 7 q / 8 ) ↦ − Q / 8 \begin{array}{lcr} (-q/8,3q/8) &\mapsto& Q/8\\ (3q/8,7q/8) &\mapsto& -Q/8\\ \end{array} (−q/8,3q/8)(3q/8,7q/8)↦↦Q/8−Q/8
我们对 L W E s ( q / 4 ⋅ ( m 1 + m 2 ) ) LWE_s(q/4 \cdot (m_1+m_2)) LWEs(q/4⋅(m1+m2)) 应用关于上述 f f f 的自举程序,然后再把它旋转 Q / 8 Q/8 Q/8 相位回到 f ′ f' f′,这就得到了 L W E k ( Q / 4 ⋅ N A N D ( m 1 , m 2 ) ) LWE_k(Q/4 \cdot NAND(m_1,m_2)) LWEk(Q/4⋅NAND(m1,m2)),最后再执行一个 Key-Switch 即可。
- 其他二元门 X O R 、 A N D 、 O R XOR、AND、OR XOR、AND、OR 的计算也都是类似的
- 一元门 N O T NOT NOT 仅仅是同态的常数加法, ( a , b ) ↦ ( − a , q / 4 − b ) (a,b) \mapsto (-a,q/4-b) (a,b)↦(−a,q/4−b)
- 三元门 M a j o r Major Major 也可以使用 Z 4 \mathbb Z_4 Z4 的算术加法来模拟,先计算 m 1 + m 2 + m 2 m_1+m_2+m_2 m1+m2+m2,然后将 0 , 1 ↦ 0 0,1 \mapsto 0 0,1↦0 以及 2 , 3 ↦ 1 2,3 \mapsto 1 2,3↦1
各种布尔函数的反循环函数 f f f 的汇总,
AP/TFHE
AP 策略的累加器 A C C f ← + c ⋅ E ( s ) ACC_f \overset{+}{\gets} c \cdot E(s) ACCf←+c⋅E(s),假设初始时 A C C f = R L W E k ( m ) ACC_f=RLWE_k(m) ACCf=RLWEk(m)
-
KeyGen 阶段:我们设置密文 c ∈ Z q c \in \mathbb Z_q c∈Zq 的 radix- B r B_r Br 分解,位数 d r = log B r q d_r=\log_{B_r} q dr=logBrq,定义形状 d r × ( B r − 1 ) d_r \times (B_r-1) dr×(Br−1) 的 RGSW 密文矩阵:
E ( s ) : = { Z j , v = R G S W k ( X s ⋅ v B r j ( m o d q ) ) ∣ j = [ d r ] , v ∈ [ B r ] , v ≠ 0 } E(s) := \{Z_{j,v}=RGSW_k(X^{s \cdot vB_r^j \pmod q})\mid j=[d_r],v \in [B_r],v \neq 0\} E(s):={Zj,v=RGSWk(Xs⋅vBrj(modq))∣j=[dr],v∈[Br],v=0}
其中的 X = x 2 N / q ∈ R Q X=x^{2N/q} \in R_Q X=x2N/q∈RQ 是循环子群生成元。实际上, E ( s ) E(s) E(s) 就是枚举了全部的 c c c 的可能取值,采取 B r B_r Br 进制分解仅仅是出于 time/space trade-off 考虑。
-
Update 阶段:我们分解 c ∈ Z q c \in \mathbb Z_q c∈Zq 成为 ∑ i c i B r i \sum_i c_i B_r^i ∑iciBri,利用 c i c_i ci 挑选 E ( s ) E(s) E(s) 的分量。迭代计算连续的外积 ∘ : R L W E × R G S W → R L W E \circ:RLWE \times RGSW \to RLWE ∘:RLWE×RGSW→RLWE,
A C C f ← A C C f ∘ Z j , c j , j = 0 , 1 , ⋯ , d r − 1 ACC_f \gets ACC_f \circ Z_{j,c_j},\,\, j=0,1,\cdots,d_r-1 ACCf←ACCf∘Zj,cj,j=0,1,⋯,dr−1容易验证迭代的最终结果是
R L W E k ( m ⋅ X s ⋅ ∑ c i B r i ) = R L W E k ( m ⋅ X s ⋅ c ) RLWE_k(m \cdot X^{s \cdot \sum c_i B_r^i}) = RLWE_k(m\cdot X^{s \cdot c}) RLWEk(m⋅Xs⋅∑ciBri)=RLWEk(m⋅Xs⋅c)
FHEW 的完整 NAND 门的同态运算如下:
GINX/TFHE
GINX 策略的累加器 A C C f ← + c ⋅ E ( s ) ACC_f \overset{+}{\gets} c \cdot E(s) ACCf←+c⋅E(s),假设初始时 A C C f = R L W E k ( m ) ACC_f=RLWE_k(m) ACCf=RLWEk(m)
-
KeyGen 阶段:我们设置私钥 s ∈ Z q s \in \mathbb Z_q s∈Zq 的 radix- U U U 分解, s = ∑ u ∈ U s u ⋅ u s=\sum_{u \in U} s_u \cdot u s=∑u∈Usu⋅u,其中 U ⊆ Z q U \subseteq \mathbb Z_q U⊆Zq 是某子集,使得 s u ∈ { 0 , 1 } s_u \in \{0,1\} su∈{0,1} 仅仅是二值的。定义长度 ∣ U ∣ |U| ∣U∣ 的 RGSW 密文向量:
E ( s ) : = { Z u = R G S W k ( s u ) ∣ s ⃗ ∈ { 0 , 1 } U , s = ∑ u u ⋅ s u } E(s) := \{Z_{u}=RGSW_k(s_u)\mid \vec s \in \{0,1\}^U,s=\sum_u u\cdot s_u\} E(s):={Zu=RGSWk(su)∣s∈{0,1}U,s=u∑u⋅su}实际上,这里 E ( s ) E(s) E(s) 就是 MUX-Gate 的控制位,[MP21] 利用自举的线性将它用 U U U 做了扩展(如果简单使用 Equality Test 构造 Multi-Input MUX,这会是一个高次多项式)。对于 { 0 , 1 } \{0,1\} {0,1} 的秘密,选取 U = { 1 } U=\{1\} U={1};对于 { 0 , ± 1 } \{0,\pm1\} {0,±1} 秘密,选取 U = { ± 1 } U=\{\pm 1\} U={±1};对于 Z q \mathbb Z_q Zq 中的秘密,选取 U = { 1 , 2 , 4 , ⋯ , 2 log 2 q − 1 } U=\{1,2,4,\cdots,2^{\log_2q-1}\} U={1,2,4,⋯,2log2q−1}
-
Update 阶段:我们根据 c c c 构造 MUX-based OBDD 为 M U X ( s , m ⋅ X 0 , m ⋅ X c ) MUX(s,m \cdot X^0,m \cdot X^{c}) MUX(s,m⋅X0,m⋅Xc),设置 Z ˉ u = G − Z u \bar Z_u=G-Z_u Zˉu=G−Zu,迭代计算
A C C f ← A C C f ∘ Z ˉ u + ( X u ⋅ c ⋅ A C C f ) ∘ Z u , ∀ u ∈ U ACC_f \gets ACC_f \circ \bar Z_{u} + (X^{u \cdot c} \cdot ACC_f) \circ Z_u,\,\, \forall u \in U ACCf←ACCf∘Zˉu+(Xu⋅c⋅ACCf)∘Zu,∀u∈U其中的 X = x 2 N / q ∈ R Q X=x^{2N/q} \in R_Q X=x2N/q∈RQ 是循环子群生成元。由于 M U X ( x , y , z ) = ( 1 − x ) ⋅ y + x ⋅ z = y + x ⋅ ( z − y ) MUX(x,y,z)=(1-x)\cdot y+x\cdot z = y+x\cdot(z-y) MUX(x,y,z)=(1−x)⋅y+x⋅z=y+x⋅(z−y),因此我们可以把上述的 MUX 化简到只需要单个外积,
A C C f ← A C C f + ( X u ⋅ c − 1 ) ⋅ ( A C C f ∘ Z u ) , ∀ u ∈ U ACC_f \gets ACC_f + (X^{u \cdot c} -1) \cdot(ACC_f \circ Z_u),\,\, \forall u \in U ACCf←ACCf+(Xu⋅c−1)⋅(ACCf∘Zu),∀u∈U容易验证迭代的最终结果是
R L W E k ( m ⋅ X c ⋅ ∑ u ⋅ s u ) = R L W E k ( m ⋅ X s ⋅ c ) RLWE_k(m \cdot X^{c \cdot \sum u \cdot s_u}) = RLWE_k(m\cdot X^{s \cdot c}) RLWEk(m⋅Xc⋅∑u⋅su)=RLWEk(m⋅Xs⋅c)
TFHE 的完整 NAND 门的同态运算如下:
Comparison
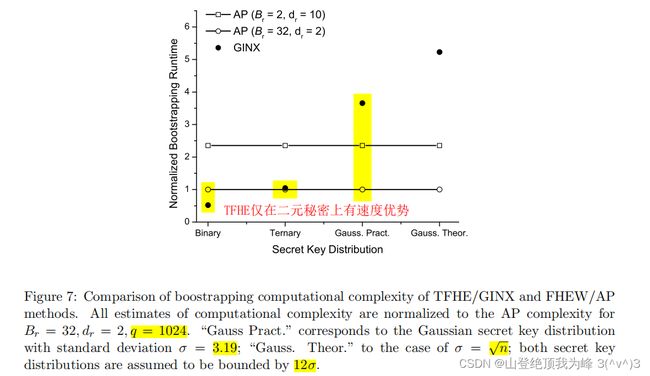
[MP21] 选择了三种私钥分布:二元均匀、三元均匀、高斯分布。对于高斯分布,依据 [ACC+18] 的建议,选择了 σ ≈ 3.2 \sigma\approx 3.2 σ≈3.2 和 σ = n \sigma=\sqrt{n} σ=n 两种设置。对于 FHEW,他们选择了 B r = 2 B_r=2 Br=2(公钥小)和 B r = 32 B_r=32 Br=32(速度快),甚至可以极端的选取 B r = q B_r=q Br=q(速度与原始 TFHE 相同,但是自举秘钥巨大)。
Runtime
我们用 R Q R_Q RQ 上的 NTT 次数,作为自举复杂度的理论估计,
- AP/FHEW:在 a a a 中有 n n n 个常数,每个 c c c 分解为 d r d_r dr 位,期望上每位有 1 / B r 1/B_r 1/Br 的概率 c j = 0 c_j=0 cj=0,每个外积的 RGSW 和 RLWE 需要 2 d g + 2 2d_g+2 2dg+2,共计需要 2 ⋅ ( 1 − 1 / B r ) ⋅ n d r ( d g + 1 ) 2\cdot (1-1/B_r) \cdot nd_r(d_g+1) 2⋅(1−1/Br)⋅ndr(dg+1) 次 NTT
- GINX/TFHE:在 a a a 中有 n n n 个常数,每个 c c c 对 U U U 累加,每个外积的 RGSW 和 RLWE 需要 2 d g + 2 2d_g+2 2dg+2,共计需要 2 ⋅ ∣ U ∣ ⋅ n ( d g + 1 ) 2\cdot |U|\cdot n(d_g+1) 2⋅∣U∣⋅n(dg+1) 次 NTT
因此,理论上的计算复杂度比值为 ∣ U ∣ ( 1 − 1 / B r ) d r \dfrac{|U|}{(1-1/B_r)d_r} (1−1/Br)dr∣U∣
TFHE 仅在二元均匀分布下具有明显的效率优势。对于三元均匀分布,TFHE 甚至比 B r = 32 B_r=32 Br=32 的 FHEW 略微慢一点儿。对于高斯分布,即使 B r = 2 B_r=2 Br=2 下的 FHEW 也比 TFHE 快不少。
Size of BK
我们用 R Q R_Q RQ 上的 NTT 次数,作为自举复杂度的理论估计,
- AP/FHEW:在 s k sk sk 中有 n n n 个秘密,每个 s s s 构造出 ( B r − 1 ) d r (B_r-1)d_r (Br−1)dr 个 RGSW 密文,每个 RGSW 密文含有 4 d g 4d_g 4dg 个环元素,每个环元素需要 N log 2 Q N\log_2Q Nlog2Q 比特存储,共计需要 4 ⋅ ( B r − 1 ) d r ⋅ n N d g log 2 Q 4\cdot (B_r-1)d_r \cdot nNd_g\log_2Q 4⋅(Br−1)dr⋅nNdglog2Q 比特
- GINX/TFHE:在 s k sk sk 中有 n n n 个秘密,每个 s s s 构造出 ∣ U ∣ |U| ∣U∣ 个 RGSW 密文,每个 RGSW 密文含有 4 d g 4d_g 4dg 个环元素,每个环元素需要 N log 2 Q N\log_2Q Nlog2Q 比特存储,共计需要 4 ⋅ ∣ U ∣ ⋅ n N d g log 2 Q 4\cdot |U|\cdot nNd_g\log_2Q 4⋅∣U∣⋅nNdglog2Q 比特
因此,理论上的公钥规模比值为 ∣ U ∣ ( B r − 1 ) d r \dfrac{|U|}{(B_r-1)d_r} (Br−1)dr∣U∣
对于二元均匀、三元均匀,TFHE 的自举秘钥规模远小于 FHEW 的。而对于高斯分布,选取 B r = 2 B_r=2 Br=2 的 FHEW 的秘钥规模与 TFHE 接近。
Recommendation
[MP21] 建议:
- 标准化 [ACC+18] 不考虑二元秘钥分布。[Mic18] 给出了 Standard LWE with Binary secrets下的归约,[EJK20] 展示了 Ring-LWE with Binary secrets 的由二元秘密的特殊性质所导致的弱点。
- 对于三元秘钥分布,采取 TFHE 自举,选择 U = { − 1 , 1 } U=\{-1,1\} U={−1,1}
- 对于高斯秘钥分布,采取 FHEW 自举,选择 B r = 2 B_r=2 Br=2 以最小化自举秘钥规模,设置高斯分布的取值范围 [ − 8 , 8 ] [-8,8] [−8,8](大约对应标准差 σ = 8 / 2 π ≈ 3.19 \sigma =8/\sqrt{2\pi}\approx 3.19 σ=8/2π≈3.19,除了概率 P r [ x > 2 π ] = e r f c ( 2 π / 2 ) ≈ 0.0122 Pr[x>\sqrt{2\pi}]=erfc(\sqrt{2\pi}/\sqrt2)\approx0.0122 Pr[x>2π]=erfc(2π/2)≈0.0122 越界)
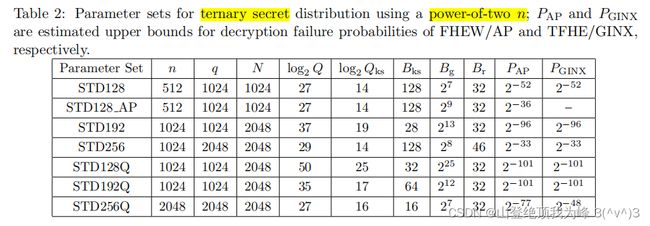
[MP21] 选取的参数集
经典 128 128 128 比特安全性参数集的效率