论文阅读:BPFINet: Boundary-aware progressive feature integration network for salient object detection
论文地址:https://doi.org/10.1016/j.neucom.2021.04.078
代码地址:https://github.com/clelouch/BPFINet
发表于:Neurocomputing 2021
I. Intro
- 这个网络是用来进行显著目标检测的
- 主要工作在于一个USRM模块进行特征的细化,CCM模块实现更好的通道注意力机制,UFIM模块提供一种特征融合的思路,以及一个Fusion Loss
II. Network Architecture

整体还是属于Encoder-Decoder框架,其中Encoder采用的是ResNet50。R代表USRM模块,C代表CCM模块,F代表UFIM模块,将在后文进行介绍
III. USRM
USRM意为U-shape self-refinement module,U型自细化模块。在网络中用到了两处:

第一处出现在Encoder与Decoder的连接处,相当于连接Encoder与Decoder的bridge,这种情景下其作用大概率是进一步处理Encoder所习到的特征;第二处出现在第一个Decoder后,其输入为第一个Decoder与倒数第二个Encoder所concat的特征。
那么为什么要做这个细化呢?
- 某个卷积层只能捕获某一特定规模的信息
- 显著对象的尺寸往往多种多样
USRM的结构如下所示:

从结构上看是一个小型的UNet。文中对其作用的阐述是,“可以让特征对scale variation更加鲁棒,从而提升网络检测小对象的性能”,但是目前我还没太弄明白为什么能有这个效果。
IV. CCM
CCM意为Channel Compression Module,通道压缩模块。这里首先有个小问题就是为什么要把CCM放在各Decoder后进行通道压缩,这是因为本文后面的特征融合用的是element wise加,那么就得先统一特征图通道数。
而谈到通道压缩,比较容易想到的就是经典的1×1卷积,其拥有对通道进行降维的能力。不过既然又单独提出了CCM模块,说明1×1卷积存在着一定的缺陷。文中指出了1×1卷积的这么个问题:
- 特征图的各个通道是class-specific的,不同通道针对不同语义进行响应[1,2]
因此,直接用1×1卷积进行降维的话,可能导致对显著区域有更高响应的通道反而被压缩掉。那么如何解决这个问题呢?
文中的做法是用注意力机制。既然一些通道更重要,那么就给予这些通道更大的权重。CCM的结构如下所示:

- C: 卷积层
- P: 全局池化层
- F: 全连接层
- ×: element-wise乘
- +: element-wise加
具体过程为,对于输入特征图 F h ∈ R C i n × H × W F_{h} \in R^{C_{i n} \times H \times W} Fh∈RCin×H×W:
- 首先经过一个1×1卷积进行降维,得到 F h 1 ∈ R C o u t × H × W F_{h1} \in R^{C_{out} \times H \times W} Fh1∈RCout×H×W
- 经过一个全局池化层,得到一个channel-wise的向量 V h 1 ∈ R C out V_{h 1} \in R^{C_{\text {out }}} Vh1∈RCout
- 再经过两个全连接层,来算channel-wise的dependency,有 V h 2 = σ ( f c 2 ( relu ( f c 1 ( V h 1 ) ) ) ) V_{h 2}=\sigma\left(f c_{2}\left(\operatorname{relu}\left(f c_{1}\left(V_{h 1}\right)\right)\right)\right) Vh2=σ(fc2(relu(fc1(Vh1))))
- 然后就是将原始降维后的结果 F h 1 F_{h1} Fh1与dependency V h 2 V_{h 2} Vh2相乘,完成加权的过程,有 F h 2 = F h 1 ⊗ F_{h 2}=F_{h 1} \otimes Fh2=Fh1⊗ Expand ( V h 2 ; F h 1 ) \left(V_{h 2} ; F_{h 1}\right) (Vh2;Fh1)
- 最后还引入了一个残差连接,以便于网络的训练。最终CCM的输出为:
F h = relu ( F h 2 + conv ( F h 2 ) ) F_{h}=\operatorname{relu}\left(F_{h 2}+\operatorname{conv} \left(F_{h 2}\right)\right) Fh=relu(Fh2+conv(Fh2)) 这里残差用的卷积是一个3×3卷积。
V. UFIM
UFIM意为U-shape feature integration module,U型特征融合模块。那么为什么要做特征融合呢?
- 高级特征包含更多的语义信息,有利于定位显著区域
- 低级特征包含更多的细节信息,有利于定位显著边界
- 在向网络浅层传递的过程中,全局特征会逐渐被稀释
UFIM的作用就是将高级特征、低级特征、全局特征给聚合起来。而说到特征聚合,最基础的一个方法就是像UNet那样,做一个skip connection,把不同的特征直接concat或者相加。然而这么做的缺陷在于:
- 三种特征的感受野差别很大,直接resize再concat或add可能并不合适
既然感受野差别很大不好直接加,那就可以想办法把三者的感受野调整至差不多,然后再加,因此UFIM便通过相应的卷积层来完成感受野调整的过程。针对不同层级的特征,UFIM的深度也有所不同,这里以最后一个UFIM为例进行说明。其中的X,Y,Z分别对应着低级特征、高级特征、全局特征:
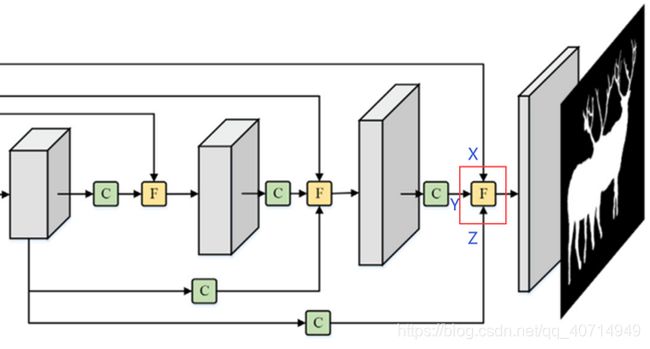
其结构示意图如下所示:

可以看到整体呈U型结构,有三个输入:
- low: 低级特征Fl,其来源于第一个Encoder的输出,尺寸为 H 2 × W 2 \frac{H}{2} \times \frac{W}{2} 2H×2W
- high: 高级特征Fh,其来源于倒数第二个Decoder的输出,尺寸为 H 4 × W 4 \frac{H}{4} \times \frac{W}{4} 4H×4W
- global: 全局特征Fg,其来源于第二个Decoder的输出,尺寸为 H 16 × W 16 \frac{H}{16} \times \frac{W}{16} 16H×16W
特征融合过程:
先看低级特征与高级特征的融合。将Fl送入3×3卷积层,扩大其感受野,得到的结果记为F(1)。此时,F(1)与Fh的感受野相近,可以直接进行element-wise加,得到F(2)。
接着是与全局特征的融合。根据特征图的尺寸,将F(2)送入两个3×3卷积层,扩大两次感受野,得到的结果记为F(3)。此时,F(3)与Fg的感受野相近,可以直接进行element-wise加。
之后则是一些skip connection的过程,在此不再进行赘述。其余两个UFIM的结构如下所示:
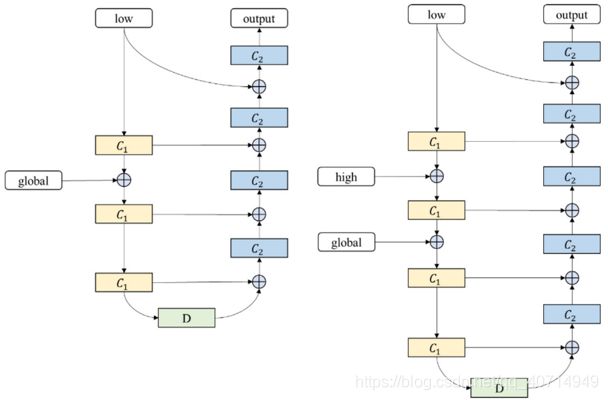
VI. Loss Function
传统BCE Loss有两个缺陷:
- 显著边界处的像素往往更难确定,因此生成的预测图在边界处经常是模糊的
- 当预测结果与ground truth完全不相交时,相应的惩罚并不大,尤其是对于小物体而言
为此本文提出了种Fusion Loss(注,由于原文此处描述可能有混淆,这里对公式表述进行了略微修改):
L all = L ( 1 ) + 0.5 L ( 2 ) + 0.25 L ( 3 ) + 0.125 ( L ( 4 ) + L ( 5 ) ) \mathscr{L}_{\text {all }}=\mathscr{L}_{(1)}+0.5 \mathscr{L}_{(2)}+0.25 \mathscr{L}_{(3)}+0.125\left(\mathscr{L}_{(4)}+\mathscr{L}_{(5)}\right) Lall =L(1)+0.5L(2)+0.25L(3)+0.125(L(4)+L(5))
由于采用了deep supervision策略,对每一个side output都进行了监督,这里的 L ( i ) \mathscr{L}_{(i)} L(i)便指第i个side output的loss。权重的设计思路是,side output的尺寸越小(或者是大?文中没有明确指明,需要查看代码),相应的权重也就越小。
接下来分析 L \mathscr{L} L的组成,有:
L = L wbce + 0.5 × ( L wiou + L woiou ) \mathscr{L}=\mathscr{L}_{\text {wbce }}+0.5 \times\left(\mathscr{L}_{\text {wiou }}+\mathscr{L}_{\text {woiou }}\right) L=Lwbce +0.5×(Lwiou +Lwoiou )
L wbce \mathscr{L}_{\text {wbce }} Lwbce 指weighted BCE Loss, L wiou \mathscr{L}_{\text {wiou }} Lwiou 指weighted IoU Loss, L woiou \mathscr{L}_{\text {woiou }} Lwoiou 指weighted opposite IoU Loss。
对于wBCE和wIoU而言,关键在于这个w要怎么去设计。设计的目标当然是给予边界处的像素更大的权重,文中的做法是:
w = conv g ( G ) w=\operatorname{conv}_{g}(G) w=convg(G)
G就是指ground truth了,而这里的卷积核采用的是一个31×31(从后文可以看出这个31是调参调出来的)的高斯核。接下来则有:
V i , j = G i , j × log ( S i , j ) + ( 1 − G i , j ) × log ( 1 − S i , j ) V_{i, j}=G_{i, j} \times \log \left(S_{i, j}\right)+\left(1-G_{i, j}\right) \times \log \left(1-S_{i, j}\right) Vi,j=Gi,j×log(Si,j)+(1−Gi,j)×log(1−Si,j) L wbce = − ∑ i = 1 H ∑ j = 1 W ( 1 + γ × w i , j ) × V i , j ∑ i = 1 H ∑ j = 1 W ( 1 + γ × w i , j ) \mathscr{L}_{\text {wbce }}=-\frac{\sum_{i=1}^{H} \sum_{j=1}^{W}\left(1+\gamma \times w_{i, j}\right) \times V_{i, j}}{\sum_{i=1}^{H} \sum_{j=1}^{W}\left(1+\gamma \times w_{i, j}\right)} Lwbce =−∑i=1H∑j=1W(1+γ×wi,j)∑i=1H∑j=1W(1+γ×wi,j)×Vi,j L wiou = 1 − 1 + ∑ i = 1 H ∑ j = 1 W ( G i , j × S i , j ) ( 1 + γ × w i , j ) 1 + ∑ i = 1 H ∑ j = 1 W ( G i , j + S i , j − G i , j × S i , j ) ( 1 + γ × w i , j ) \mathscr{L}_{\text {wiou }} = 1-\frac{1+\sum_{i=1}^{H} \sum_{j=1}^{W}\left(G_{i, j} \times S_{i, j}\right)\left(1+\gamma \times w_{i, j}\right)}{1+\sum_{i=1}^{H} \sum_{j=1}^{W}\left(G_{i, j}+S_{i, j}-G_{i, j} \times S_{i, j}\right)\left(1+\gamma \times w_{i, j}\right)} Lwiou =1−1+∑i=1H∑j=1W(Gi,j+Si,j−Gi,j×Si,j)(1+γ×wi,j)1+∑i=1H∑j=1W(Gi,j×Si,j)(1+γ×wi,j)
最后,wIoU作为map level的指标,在显著对象较小时效果较好,而显著对象较大时则作用减弱,因此这里还引入了一个woIoU:
L woiou = 1 − 1 + ∑ i = 1 H ∑ j = 1 W ( G i , j ‾ × S i , j ‾ ) ( 1 + γ × w i , j ) 1 + ∑ i = 1 H ∑ j = 1 W ( G i , j ‾ + S i , j ‾ − G i , j ‾ × S i , j ‾ ) ( 1 + γ × w i , j ) \mathscr{L}_{\text {woiou }} = 1-\frac{1+\sum_{i=1}^{H} \sum_{j=1}^{W}\left(\overline{G_{i, j}} \times \overline{S_{i, j}}\right)\left(1+\gamma \times w_{i, j}\right)}{1+\sum_{i=1}^{H} \sum_{j=1}^{W}\left(\overline{G_{i, j}}+\overline{S_{i, j}}-\overline{G_{i, j}} \times \overline{S_{i, j}}\right)\left(1+\gamma \times w_{i, j}\right)} Lwoiou =1−1+∑i=1H∑j=1W(Gi,j+Si,j−Gi,j×Si,j)(1+γ×wi,j)1+∑i=1H∑j=1W(Gi,j×Si,j)(1+γ×wi,j)
落实到实验中,可以观察到,在显著目标较大时,wBCE占主导,woIoU的值也较大;在显著目标较小时,wIoU占主导。
VII. Experiment
性能超越了16个最近模型,包括Amulet(ICCV 2017)、UCF(ICCV 2017)、NLDF(CVPR 2017)、PAGR(CVPR 2018)、BMPM(CVPR 2018)、R3Net(IJCAI 2018)、PICANet-R(CVPR 2018)、BASNet(CVPR 2019)、CPD-R(CVPR 2019)、PoolNet(CVPR 2019)、SCRN(ICCV 2019)、CSNet(ECCV 2020)、GateNet(ECCV 2020)、DFI(TIP 2020)、GCPANet(AAAI 2020)、U2Net(PR 2020)
VIII. Summary
这篇文章的落脚点还是在这个经典问题上,即在SOD中怎么进行更好的特征融合。为此,文中的核心思路是用了三个UFIM模块,分别完成一次全局特征与低级特征的融合、两次全局特征、低级特征、高级特征的融合(注意这两次中的全局特征略有不一样),实现更好的性能。至于其他的有个CCM,其性能比PFAN、 CBAM这两种通道注意力模块要更好,以及一个引入了通过weight来提升边缘处显著检测性能的Fusion Loss。
Ref
[1] T. Zhao, X. Wu, Pyramid feature attention network for saliency detection, in: Proc. IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit., 2019. https://doi.org/10.1109/CVPR.2019.00320.
[2] J. Hu, L. Shen, S. Albanie, G. Sun, E. Wu, Squeeze-and-Excitation Networks, IEEE Trans. Pattern Anal. Mach. Intell. 42 (8) (2020) 2011–2023, https://doi.org/10.1109/TPAMI.3410.1109/TPAMI.2019.2913372.