论文笔记：Coloured Ring Confidential Transactions

https://link.springer.com/chapter/10.1007/978-3-030-00305-0_14

摘要

提出了一种新的交易类型，它可以在共同的区块链上实现保护隐私的独立资产交易。

1. 实现：通过将环机密交易扩展为对颜色的附加承诺和公开可验证的保全证明来实现的。
2. 优点：通过有色机密环签名，可以引入新的代币类型，并且任何参与者都可以在使用与单代币隐私感知区块链相同大小的匿名集的情况下进行转账。因此系统可以在不损害交易隐私的情况下追踪资产在不可更改的账本上的情况。

简介

• 构建具有多个共存的资产类型，也称为颜色。
• 一笔交易可以转移恰好一种颜色，但伪装输入可以来自任何颜色，具有与单一颜色隐私感知区块链相同的匿名集。交易的颜色仅对交互方（当前交易的发送方和接收方）可见，而对其他人不可见，从输入到输出实现了对颜色保全的全面隐私感知验证。
• 借助新的交易类型，区块链的所有参与者都可以为自己的目的引入新的代币类型。共识验证新的颜色尚不存在，以防止未经授权的现有代币发行。

优势：所有新代币都将受益于隐私感知交易，而无需创建每种颜色的独立链的障碍。每种颜色的新区块链减少了交易中伪装的机会，从而对整个系统的隐私产生负面影响。此外，单个区块链上的多个颜色有助于未来在链上进行颜色之间的原子交换操作。

Preliminaries

门罗币中所使用的：

• Pedersen Commitments
• MLSAG

Coloured Ring Confidential Transaction

ringCT交易在 Monero 中广泛用于 RCTTypeFull，这篇论文扩展RCTTypeFull ringCT以支持交易的输入和输出的颜色属性。扩展的部分标红。

In- and Outputs

• 公钥：发送者选择要使用的$m$ 个输入。额外选择了 $m\cdot (n-1)$ 个输入。每个输入包含一个公钥 $P_i^j$，该公钥是作为一次性付款地址生成的。
• 金额：每个输入所持有的金额 $a$ 存储在一个带有遮蔽因子 $b$ 的 Pedersen 承诺 $C_i^j(a,b)$ 中。
• 发送者只知道对其控制的输入$(P_{\pi }^j=x_{j}G,C_{\pi }^j(a_{j,in},b_{j,in}))$的 $a_{j,in}$ 和 $b_{j,in}$ 以及 $x_j$。所有真实的输入组成了一个在秘密索引$\pi$下的向量:
  
  在$i=1,...,\pi -1,\pi +1,...,n$ 处的伪装向量被平等地组装，既不知道 $P_i^j$ 的私钥，也不知道 Pedersen 承诺 $C_i^j$的盲因子和金额。

扩展的部分：

• 引入颜色属性作为每个输入中的额外承诺。颜色被定义为标量 $f_i$。每个输入都得到一个到颜色的额外承诺 $F_i^j$。
• 对于发送者拥有的输入，颜色 $f_{j,in}$ 和承诺 $F_{\pi }^j(f_{j,in},u_{j,in})$ 的盲因子 $u_{j,in}$ 是已知的。现在，一个输入$(P_{\pi }^j,C_{\pi }^j(a_{j,in},b_{j,in}),F_{\pi }^j(f_{j,in},u_{j,in}))$由接收者的一次性密钥和两个承诺组成。
• 交易的 $q$ 个输出也表示为一个包含三个元素的元组$(P_k,C_k(a_{k,out},b_{k,out}),F_k(f_{out},u_{k,out}))$，其中 $k=1,...,q$，且 $b_{k,out}$和 $u_{k,out}$ 是随机绘制的秘密盲因子。

交易守恒

所有输入进入交易的金额之和必须始终大于或等于所有输出金额之和，因此明文方程${\sum }_{j=1}^m{a}_{j,\text{in}}-{\sum }_{k=1}^q{a}_{k,\text{out}}=0$转化为一个承诺方程：

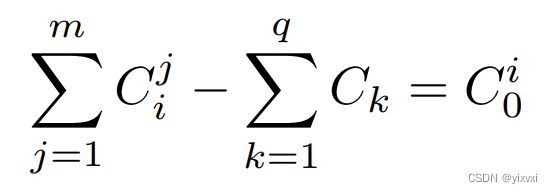
得到一个对零的承诺 $C_0^i$。

• 对于$i=\pi$，签名者知道所有的金额 $a_{j,in}$ 和盲因子 $b_{j,in}$，它们构成了对 $C_0^{\pi }$ 的私钥。这种保存确保在交易中不会创建任何资产。

• 为确保真实的输入都来自相同的颜色，颜色承诺$F_i^j$ 在成对地与第一个输出的颜色承诺 $F_1$ 进行检查。同样，我们可以使用一个对零的承诺 $F_i^j-F_1=F_0^{i,j}$，而不会透露颜色。

• 与金额总和的求和不同，使用同态性质比较累积承诺并不安全，可能导致以下攻击。攻击者创建一个具有两个输入颜色 $f_{in-}$ 和 $f_{in+}$ 以及一个输出 $f_{out}$的交易。如果我们只验证 $f_{in-}+f_{in+}=2f_{out}$，那么输入未必来自相同的颜色。所以这种保存规则仅支持每个交易一个颜色。

Signature

从金额的 $n$ 个承诺和颜色检查的$n\cdot m$个承诺可以通过MLSAG 进行签名。
注意新引入的项：

由于发送者知道将支出密钥 $P_{\pi }^j$ 和颜色、价值承诺的分量的私钥 $x_j$，它仍然可以使用 $x_{m+1+j}=x_j+f_{j,in}-f_{1,out}$对承诺和 $P_{\pi }^j$ 的总和进行签名。

Output Proofs.

ringCT 使用范围证明将输出金额限制在区间 $[0,2^{64}]$。本方案的扩展必须确保所有输出都是对相同颜色的承诺。通过为零承诺 $F_1-F_k=F_0^k$（其中$k=2,...,q$）附加 $q-1$ 个签名来实现这一点。

Discussion

这项扩展方案对整个系统隐私的影响。

Size and Performance Overhead.

• 原本MLSAG 签名需要 $(n(m+1)+1+m)32+ϵ$ Bytes，其中 $ϵ$ Bytes 是环成员的可变长度编码位置的大小。
• $q$个输出需要$q(1+64\cdot 2+64)32$ Bytes，用于 Borromean 范围证明，包括证明 64 位范围的签名和承诺。

扩展增加的代价：

• 签名大小增加了$n\cdot m$ 个额外的随机值 $s_{1,m+2},...,s_{1,m+1+m},...,s_{n,m+2},...,s_{n,m+1+m}$（因为需要进行环签名的数据增加了$m$组），达到 $(n(m+1+m)+1+m)32+ϵ$ Bytes。
• 金额的范围证明保持不变。
• 为了证明输出的颜色都相同，我们需要额外的 $q-1$ 个签名，用于成对的零承诺。

性能：

• 范围证明占用了当前交易的大部分空间，因此这个方案对签名大小的增加相当微不足道。只有在输入数量很大的情况下，影响才会显著。
• 仅比较签名大小，这个新方法需要大约两倍的空间。
• 随着 Bulletproofs 的引入，范围证明大小将不再线性增加，而是对数级增加，导致颜色开销更大的影响。

安全性

这个构建在未经修改的情况下使用了 MLSAG 和 Pedersen 承诺作为黑匣子，并且因此可以依赖于这些原语提供的保证。

• 在具有多个输入的交易中，如果攻击者知道引用的输入具有不同的颜色，他可以将这些输入从匿名集中排除（how?假设不同输入的匿名环颜色集合的交集小于环规模，则可以去掉其差集部分）。
• 假设颜色的交易具有最坏情况下的均匀分布，选择具有相同颜色的完整伪装向量的概率为 $1/{\chi }^m$，并随着输入数量 $m$ 和总共 $\chi$种颜色的增加而减小。（这个结论没太明白，输入本来就是需要同个颜色，而伪装集合可以任意选择）
• 对于由幂律模型建模的交易频率的更有可能的分布，其中大多数输出具有本地颜色，找到一个单一颜色的伪装的概率更高。对于一个具有两个输入的交易和总共有合理的 200 种颜色的情况，Zipf 分布的结果是在每 20 个伪装向量中有 2 种相同颜色的概率约为一。

初始颜色创建。

为了能够传输具有隐私意识的有色代币，首先需要一个代币发行协议。一种简单的方式是允许在交易中增加一个附加输出，为输出地址授予一个新颜色中的定义数量的代币。通过公开颜色承诺，仅当颜色相对于所有先前的颜色初始化交易而言是新的时，交易才有效。根据新代币类型的使用情况，金额可以是一个公开的承诺，以公开宣布代币的总供应量，或者如果不需要，则可以是机密的。