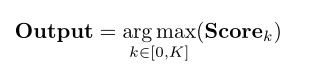【论文阅读笔记】Large language models are reasoners with self-verification

Abs

在LLM上提出了一个基于CoT的自我验证的方法来模仿人类的验算，并证明了它有用。

原文：当一个大型语言模型(LLM)通过思维链(CoT)执行复杂推理时，它可能对个别错误高度敏感。为了解决这个问题，我们不得不培训验证人员(verifiers)。我们都知道，人类在推断出一个结论后，通常会通过重新验证来检查它，这可以避免一些错误。我们提出了一种称为自我验证的新方法，使用CoT的结论作为条件来构建一个新的样本，并要求LLM重新预测被掩盖的原始条件。我们根据准确性计算一个可解释的验证分数。该方法在使用少镜头学习时，可以提高多个算术和逻辑推理数据集的精度。我们已经证明LLM可以对自己的结论进行可解释的自我验证，并实现竞争推理性能。大量的实验证明，我们的方法可以帮助多个大型语言模型进行自我验证，避免错误CoT的干扰。

Intro

文章思路来源的图示（一个例子）：

CoT的作用是模拟人类思维推导的过程，指导LLM为多步骤问题生成中间推理步骤（而不仅是最后结果），从而提高LLM的推理能力，在一些任务中已经超过了SOTA。CoT的一个大问题是缺乏鲁棒性，一个小错误就可能把它带偏。

之前的解决办法是训练verifiers，这种方法有三个缺点，一是需要太多人力和计算资源，二是可能会有假阳性（错误的思维过程推理出正确答案），三是不好用输出的分数来评估模型可靠性。

所以文章提出用LLM的自我验证能力来进行验算。思路是：假设推理问题中的所有条件都是结论的必要条件，那么给定结论和部分条件，应该能反推出剩下的条件。（如上图所示）

分为两个阶段：1. 正向推理（正常生成候选的CoT和结论）2. 反向验证（用LLM验证条件是否满足候选结论，并根据验证分数对候选结论排序）

这样的话就能对应上面的三个缺点了：消耗的资源不高；用候选结论验证，解决了CoT中偏离正确思维过程的过程；验证分数来自整个思维推导过程，具有高度解释性。

作者用GPT-3、CODEX和derective-gpt做了实验，证实有显著分数提高。

Related Work

没啥特别的

Method

先来一个例子：

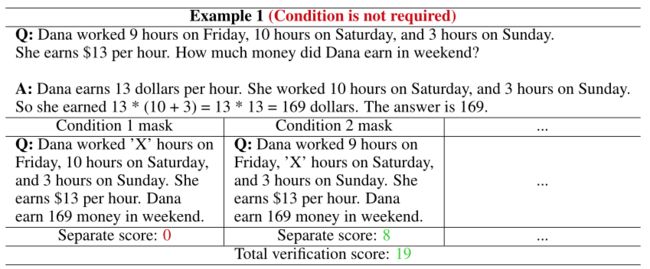
第一阶段（stage1）中，左侧是问题（一天读4本书，每周一和周二读书，6周能读多少书），右侧是候选思维过程和结论（思维过程A1：一天读4本，一周7天，6周读6*7*4=168本；……；思维过程Ak：一天读4本，每周一和周二读，相当于一周有两天，所以每周读4*2=8本，6周读8*6=48本）

第二阶段（stage2）中，对stage1中的结论一一验证，左侧是stage1中的结论和一部分条件，右侧是需要反推的条件，如A1，将6周读了168本和每周一周二读书作为条件，一天读几本书作为问题，反推得到一天读14本（错误），但Ak就能得到正确答案（4本）。

---

候选结论生成：M是语言模型，D是数据集（包含问题和结论），C是CoT为D生成的包含 n 个样本的样本集（n一般是个位数），其中每个样本都有一个输入X，X包含条件、问题、思维过程 t 和结论 y，模型需要先生成t，然后反复采用抽样解码生成k个y（候选结论）。生成的概率如下：

重写结论和条件：X={f1,f2,....,fR,q}（f是条件，q是问题），使用命令

依次验证：轮流验证，把所有f都验证一次，因为某个条件未必是结论的必要条件（如下图），会干扰评分。

计算验证分数：

Experiment Setting

任务和数据集：6个算术推理数据集，1个常识推理数据集，1个逻辑推理数据集。

模型：the original CODEX，the Instruct-GPT

Prompt：没看懂

Implementation：也没看懂

Result

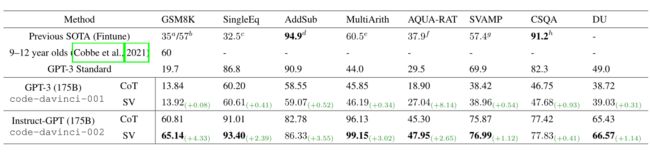
本文的方法在六个任务中实现了SOTA性能，对算术数据集的改进尤其大。

下图是在六个算数数据集上的实验，因为输入的每个数字都能视为一个条件，所以用它们来研究增加验证条件数量的影响。在大多数实验中，多条件验证比单条件验证表现更好，而且两者都比原始CoT表现好。

下图是实验不同尺寸的模型是否具有自我验证的能力，实验结果显示参数较小的时候模型的自我验证能力较弱。说明自我验证能力将出现在更大的模型中。

下图是实验CoT少会不会影响自我验证的性能，证明样本越小鲁棒性越强。

除了条件掩码，还有别的方法来验证吗？如图所示，作者尝试了用真假来验证，但是效果远远不行。

 剩下的懒得写了