一文搞懂 归并排序及求解逆序对 真简单

排序算法有很多，比如冒泡排序、选择排序、插入排序、快速排序、堆排序、归并排序、希尔排序、桶排序、基数排序，其中归并排序的最坏、最好、平均时间复杂度均为O(nlogn)，是一种稳定排序的算法。

归并排序思想

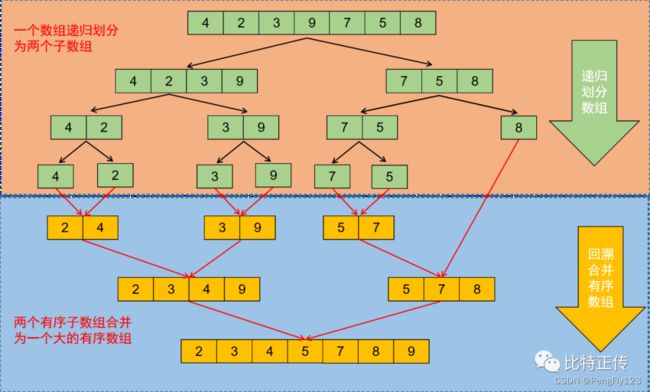
Step1：通过递归的方式，将数组进行划分（每次将一个数组从中间一分为二，左子数组和右子数组），直到子数组的长度小于等于1停止，此时子数组一定是有序的（长度小于等于1的数组一定有序）；

Step2：通过Step1一直递归直到子数组长度小于等于1，然后将两个有序子数组合并为一个有序数组，继续往上回溯，直到整个数组有序；

Step3：在Step2中，如何合并两个有序子数组呢？很简单，开一个新的临时数组，按顺序依次将两个子数组遍历，从小到大依次放入临时数组中，然后将有序的临时数组回填到原数组中，使得原数组有序。

演示图

代码code

#include "bits/stdc++.h"
using namespace std;
const int N = 1e5+10;
int a[N];
int n;

void merge(int l, int r, int mid) {
  int tmp[r-l+1];  // 先新建一个临时数组，用于合并两个子数组
  int idx = 0;  // idx指向临时数组tmp，将要存放元素的位置
  int i = l, j = mid+1;  // i指向左子数组的起点，j指向右子数组的起点
  int m = r-l+1;   // 数组[l, r]加起来总共有m个元素
  while(idx < m) {   // 开始合并两个有序子数组为一个有序数组
    if(i>mid) tmp[idx++] = a[j++];  // i>mid说明左子数组的元素全部遍历完毕了，因此直接把右数组的元素放入
    else if(j > r) tmp[idx++] = a[i++];// j > r说明右子数组的元素全部遍历完毕了，因此直接把左数组的元素放入
    else {  // 否则说明两个子数组均还有元素要放入tmp，那就比大小，谁小放谁
      if(a[i]>a[j]) tmp[idx++] = a[j++];  
      else tmp[idx++] = a[i++];
    }
  }
  for(int i=0; i= r) return ;  // 子数组[l, r]只有一个元素或者为空即停止
  int mid = l + ((r-l)>>1);  // 找数组[l, r]的中点mid，将数组[l,r]划分为子数组[l, mid]和子数组[mid+1, r];
  guibin_sort(l, mid);  // 左子数组递归划分
  guibin_sort(mid+1, r);  // 右子数组递归划分
  merge(l, r, mid);
  return;
}

 int main() {
  cin >> n;
  for(int i=1; i<=n; i++) cin >> a[i];
  guibin_sort(1, n);  // 传入数组的起始和终止下标，闭区间
  for(int i=1; i<=n; i++) cout << a[i] << " ";
  return 0;
}

归并排序就算完成了，归并排序算是有固定模板的，自己也写写吧，写多了自然就会了。

写完在洛谷上可以测试，测试链接：

https://www.luogu.com.cn/problem/P1177

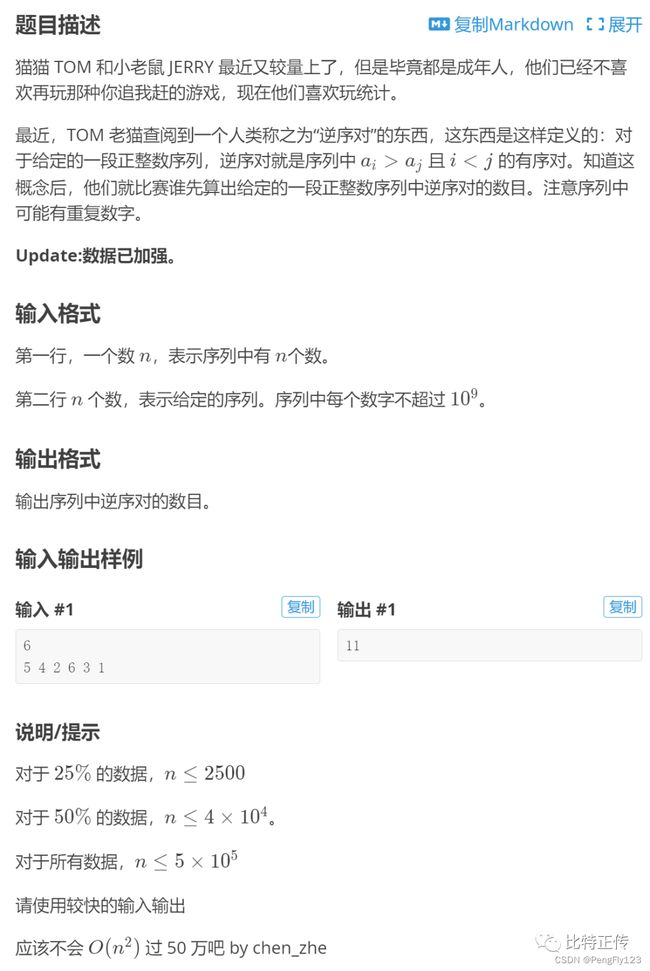
逆序对

题目链接：

https://www.luogu.com.cn/problem/P1908

题目很简单，可以用暴力做，但是暴力时间复杂度为O(n^2)，当n=5*10^5肯定会超时，所以可以借助归并排序求解。

假设(x, y）为逆序对，则x>y;

试想在归并排序的合并数组的时候，如果出现左子数组中的a[i]大于右子数组中的a[j]时，由于左子数组是有序的，因此左子数组中a[i]后面的元素都大于a[j]，因此以a[j]为y的逆序对有(a[i], a[j]), (a[i+1], a[j]),...,(a[mid], a[j]), 共mid-i+1个；

所以只需要在归并排序代码的基础上加一行就可以求解出逆序对，代码如下：

#include "bits/stdc++.h"
using namespace std;
const int N = 5e5+10;
int a[N];
int n;
long long cnt;

void merge(int l, int r, int mid) {
  int tmp[r-l+1];  // 先新建一个临时数组，用于合并两个子数组
  int idx = 0;  // idx指向临时数组tmp，将要存放元素的位置
  int i = l, j = mid+1;  // i指向左子数组的起点，j指向右子数组的起点
  int m = r-l+1;   // 数组[l, r]加起来总共有m个元素
  while(idx < m) {   // 开始合并两个有序子数组为一个有序数组
    if(i>mid) tmp[idx++] = a[j++];  // i>mid说明左子数组的元素全部遍历完毕了，因此直接把右数组的元素放入
    else if(j > r) tmp[idx++] = a[i++];// j > r说明右子数组的元素全部遍历完毕了，因此直接把左数组的元素放入
    else {  // 否则说明两个子数组均还有元素要放入tmp，那就比大小，谁小放谁
      if(a[i]>a[j]) {
        tmp[idx++] = a[j++];  
        cnt += (mid-i+1);  // 只需要加这一行就可以统计出逆序对的数量
      }
      else tmp[idx++] = a[i++];
    }
  }
  for(int i=0; i= r) return ;  // 子数组[l, r]只有一个元素或者为空即停止
  int mid = l + ((r-l)>>1);  // 找数组[l, r]的中点mid，将数组[l,r]划分为子数组[l, mid]和子数组[mid+1, r];
  guibin_sort(l, mid);  // 左子数组递归划分
  guibin_sort(mid+1, r);  // 右子数组递归划分
  merge(l, r, mid);
  return;
}
 
 int main() {
  cin >> n;
  for(int i=1; i<=n; i++) cin >> a[i];
  guibin_sort(1, n);  // 传入数组的起始和终止下标，闭区间
  cout << cnt << endl;
  return 0;
}