【数模百科】一篇文章讲清楚模拟退火算法
本篇文章节选自 模拟退火算法 - 数模百科，如果你想了解更多有关智能优化算法的信息，请移步 智能优化算法 - 数模百科
白话文
模拟退火算法，其实是受到了物理里面退火过程的启发。退火，说的是金属或者玻璃加热后再慢慢冷却，这样做能让材料更稳定，结构更完美。那这个算法就借鉴了这一点，目的是为了解决一些特别复杂的优化问题，比如说要在一大堆可能的方案中找到最好的那一个。
有时候我们要解决的问题就像是在一个多山的地图上找一个最低的点，这个点就代表了最好的解决方案。但问题是，这图上的山峰和山谷多得很，我们很容易就困在一个小山谷里出不来，以为这里就是最低点了，其实不是，外面可能还有更低的。
这时候模拟退火算法就派上用场了。它开始的时候会允许自己跳得比较随意，甚至有时候往更高的地方跳，这样就不容易被困在小山谷里。随着时间的推移，它跳来跳去的幅度会慢慢变小，这样它就能细致地在一个小区域内找到真正的最低点。就像是退火过程中，温度慢慢降低，金属的内部结构逐渐稳定下来一样。
这个算法特别适合用在那些标准的方法不好使，或者解决方案特别多、特别复杂的问题上。比如说旅行商问题，就是要找一个最短的路线让旅行商拜访所有城市，再比如说电路板设计里的布线问题，还有很多其他的工程和科学问题也都可以用。总之，当你面对的问题像一座座山峰让你头大，不知道从哪下手的时候，模拟退火算法就能出马，帮你找到一个不错的解决方案。
我们来举个例子。
你刚搬到一个新城市，这个城市里有成千上万家餐厅。你的目标很简单：找到全城最好吃的那家餐厅。但问题是，你不可能一家一家去试，那样太费时间也费钱了。
这时候，模拟退火算法就像是你的一位聪明的朋友，一开始他可能会提议说：“咱们随便选一个区域，先去那儿的一家餐厅试试。”你们可能会去一家评价还不错的餐厅，尝尝菜品。吃完之后，这位朋友可能会说：“这家还行，不过我听说隔壁区有一家更好的，要不要试试看？”即便这家餐厅已经很不错，他依然会鼓励你尝试新的地方，哪怕有时候可能会遇到不那么好的餐厅。
随着你们尝试的餐厅越来越多，你的这位朋友会越来越有感觉，他开始更有针对性地推荐：“咱们这次就在这附近找找吧，感觉好餐厅应该就在这一块。”慢慢地，他带你的尝试范围开始变小，你们开始在最有潜力的那几个区域反复尝试不同的餐厅。
最终，经过多次的尝试和比较，你们发现了那家口味最符合你心意的餐厅。这个过程里，你的朋友就像模拟退火算法一样，一开始允许一些随机和大范围的尝试，然后逐渐变得更加专注和精确，直至找到最满意的结果。
这个过程跟你在城市中寻找最好的餐厅的经历很相似，模拟退火算法就是通过这样一种逐渐收敛的探索过程，帮助解决复杂的优化问题。
定义与详解
模拟退火算法（Simulated Annealing，SA）是一种启发式算法，用来寻找在大搜索空间内的全局最优解。这种算法的设计灵感来源于金属退火的过程。在物理学中，当金属加热后再慢慢冷却时，原子会逐渐排列成最低能量的结构，这就是最稳定的状态。
初始化阶段
-
选择一个初始解：我们先随机选一个解作为起点，记为
。 -
设置初始温度：这里的温度不是实际的温度，而是一个控制参数，我们记为
。 -
确定终止温度：这个温度
是一个阈值，当当前温度降到这个值或以下时，算法就可以停止了。
搜索与接受新解阶段
-
局部搜索：在当前解 x 的周围找一个新的解
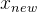。这个过程就像在当前解的周围随机走动，希望能找到更好的解。 -
Metropolis准则：这个准则决定了是否接受新解。具体来说：
-
如果
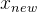比 x 更好，那么我们就接受 。 -
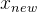如果
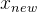比 x 更差，我们也有可能接受它，但接受的概率是
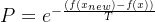，其中 ( f(x) ) 是目标函数， T 是当前的“温度”。
-
退火与终止阶段
-
降温：每走一步或几步后，我们就根据一个规则来降低温度，这个规则可以是线性的也可以是非线性的。一个常见的规则是
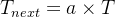，其中 0 < a < 1 是一个常数。 -
终止条件：算法会在满足一定条件时停止，这些条件可以是：
-
达到了最大的迭代次数。
-
当前温度 T 已经小于终止温度
。 -
连续几次迭代后，解没有发生太大变化。
-
通过以上步骤，模拟退火算法能够在可能接受较差的解的同时寻找最优解，这有助于它跳出局部最优并朝向全局最优解前进。随着“温度”逐渐降低，算法接受较差解的能力也会减弱，从而使解趋向稳定。就像金属冷却后原子逐渐稳定在最低能量的状态，算法最终也能找到问题的一个非常好的解。
代码
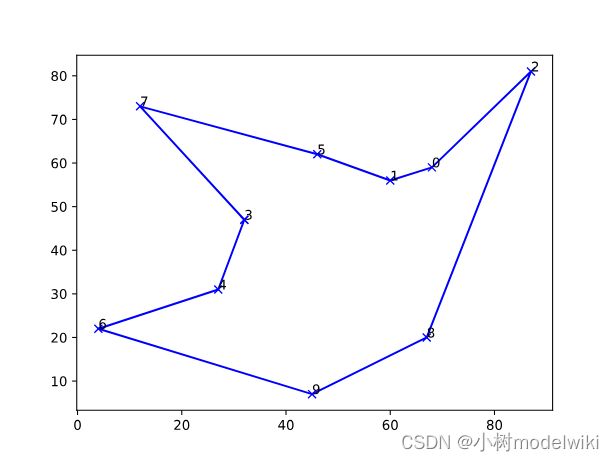
给定一系列城市和每对城市之间的距离，寻找一条最短的路径，使得旅行商开始于某城市，经过所有其他城市恰好一次，并在结束该路径时回到原始城市。
from simanneal import Annealer
import random
import numpy as np
import matplotlib.pyplot as plt
class TravelingSalesmanProblem(Annealer):
def move(self):
a = random.randint(0, len(self.state) - 1)
b = random.randint(0, len(self.state) - 1)
self.state[a], self.state[b] = self.state[b], self.state[a]
def energy(self):
e = sum(
dist_matrix[self.state[i-1]][self.state[i]]
for i in range(city_num)
)
return e
# 初始解（即初始城市访问顺序），随机产生
init_state = list(range(city_num))
random.shuffle(init_state)
tsp = TravelingSalesmanProblem(init_state)
tsp.set_schedule(tsp.auto(minutes=.2))
state, e = tsp.anneal()
print('最短总距离为：', e)
print('最佳路径为：', state)
# 使用 matplotlib 绘图
order_by_best = list(map(int, state)) + [int(state[0])]
plt.plot([cities[i][0] for i in order_by_best], [cities[i][1] for i in order_by_best], 'xb-')
for city, pos in cities.items():
plt.text(pos[0], pos[1], str(city))
plt.show()输出结果：
最短总距离为： 296.249882020428
最佳路径为： [3, 4, 6, 9, 8, 2, 0, 1, 5, 7]
优缺点
优点：
-
全局搜索能力：模拟退火算法能够在解空间中进行全局搜索，避免陷入局部最优解。
-
算法相对简单：相对于一些复杂的优化算法，模拟退火算法相对简单直观，易于理解和实现。
-
可并行化：模拟退火算法可通过多次执行并行进程来提高求解效率。
-
适应性和灵活性：模拟退火算法具有一定的适应性和灵活性，能够对问题的特性进行调整和适应。
缺点：
-
参数选择：模拟退火算法中的参数选择对其性能和结果有很大影响，需要进行合适的参数调优。
-
求解时间：模拟退火算法相对较慢，尤其在解空间复杂和目标函数复杂的情况下。
-
可能存在近似解：模拟退火算法可能找到接近最优解但不是最优解的结果，涉及一定的误差和近似性。
本篇文章节选自 数模百科 —— 模拟退火算法
数模百科是一个由一群数模爱好者搭建的数学建模知识平台。我们想让大家只通过一个网站，就能解决自己在数学建模上的难题，把搜索和筛选的时间节省下来，投入到真正的学习当中。
我们团队目前正在努力为大家创建最好的信息集合，从用最简单易懂的话语和生动形象的例子帮助大家理解模型，到用科学严谨的语言讲解模型原理，再到提供参考代码。我们努力为数学建模的学习者和参赛者提供一站式学习平台，目前网站已上线，期待大家的反馈。
如果你想和我们的团队成员进行更深入的学习和交流，你可以通过公众号数模百科找到我们，我们会在这里发布更多资讯，也欢迎你来找我们唠嗑。