MATLAB - 卫星自旋的模型参考自适应控制（MRAC）

系列文章目录

---

前言

本例展示了如何使用模型参考自适应控制 (MRAC) 控制卫星自旋，使未知控制系统与理想参考模型相匹配。卫星系统在 Simulink® 中建模，MRAC 控制器使用 Simulink Control Design™ 软件提供的模型参考自适应控制模块实现。

---

一、卫星旋转控制系统

在本例的模型中，卫星的圆柱体以恒定的角速率 ω 绕其对称轴（z 轴）旋转 [1]。目标是利用力矩 ux 和 uy 独立控制绕 x 轴和 y 轴的角速率 ωx 和 ωy。运动方程产生了一个具有两个输入和两个输出的二阶模型。

在该系统中，控制器并不直接观察被控对象的状态。相反，它通过以下测量模型间接观察状态。

在本例中，假设实际的被控对象模型未知，MRAC 控制器使用以下名义的被控对象动态模型。

鉴于这个不确定的非线性系统，您的目标是设计一个控制器，使系统能够跟踪以下解耦参考模型。

这里

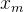• 是参考模型状态向量。
• r(t) 包含角速率参考信号。

二、定义标称模型和参考模型

定义卫星系统的动态模型。对于该系统，A 代表真实状态矩阵。

a = 10;                % System Constant
A = [0 a;-a -a/2];     % True model parameters
B = eye(2);
C = [1 a;-a 1];
D = zeros(2,2);

指定被控对象失配矩阵。该矩阵将从真实 A 矩阵中减去，从而定义控制器使用的标称被控对象。控制器的目标就是模拟这一被控对象的不确定性。

deltaA = [0 0.5*a; -0.5*a 0];   % Plant mismatch

参考系统是以下稳定的二阶系统。

Am = [-5 0; 0 -5];    % Second-order decoupled integrator model
Bm = diag([5 5]);     % Nominal control effective matrix

确定卫星自旋速率和参考模型状态的初始条件。

x1_0 = 0.5;     % Initial x-axis angular rate (rad/s)
x2_0 = 0.5;     % Initial y-axis angular rate (rad/s)
xm_0 = [0;0];   % Initial conditions of the reference plant model  

三、模型参考自适应控制结构

MRAC 控制器的目标是实现跟踪误差 的渐近收敛。

MRAC 控制器的结构如下

这里

• kx 包含反馈控制增益。
• kr 包含前馈控制增益。
• uad 是一个自适应控制项，用于消除模型的不确定性。

模型参考自适应控制模块调整自适应控制项，以实现所需的参考模型跟踪。您还可以选择调整反馈和前馈控制增益。

在本例中，控制器调整了反馈增益，并保持前馈增益不变。

初始反馈增益和静态前馈增益的计算满足以下模型匹配条件：

指定计算出的控制器增益和反馈增益学习率。

Kx = -place(A,B,eig(Am));  % State feedback gain for pole placement
gain_kx = 1;               % Feedback gain learning rate
Kr = Bm;                   % Feedforward gain for ref model matching

四、配置不确定性估计参数

MRAC 控制器在线估计模型的不确定性，并生成自适应控制动作 uad 以消除不确定性，从而恢复基线控制器的标称系统。自适应控制项使用以下模型对系统不确定性进行建模。

此处

• w 包含由控制器调整的网络权重。
• ϕ(x) 是不确定性模型特征向量。

使用模型参考自适应控制模块，您可以选择以下特征向量定义之一。

• 系统状态，其中 ϕ(x)=x(t)
• 具有高斯核的径向基函数
• 由可选输入端口提供的自定义特征。

在本例中，控制器被配置为使用系统状态作为干扰模型特征。

定义模型估计学习率 gamma_w 和跟踪误差权重 Q。

gamma_w = 100;  % Learning rate
Q = 10;         % Tracking error weight

五、模拟控制器

打开卫星旋转控制系统的 Simulink 模型。

mdl = "satellitespin";
open_system(mdl)

 仿真模型。

Tf = 35;        % Duration (s)  
sim(mdl);

通过比较自旋响应（上图）和自旋速率响应（下图）与各自的参考信号，查看控制器性能。

MRAC 控制器能很好地跟踪参考信号。第一步响应有一个初始瞬态，随着控制器对干扰估计的改进，瞬态的大小会减小。

查看控制器估计的不确定性，并将其与真实的不确定性进行比较。

控制器估算出准确的 y 轴不确定性模型。x 轴的不确定性模型符号正确，但幅度低于真实的不确定性。这两个不确定性模型的不确定性估计值都有明显的瞬变，尤其是在参考信号发生第一步变化时。

例如，将 Q 值降至 1 并模拟模型。

Q = 1;
sim(mdl);

 

 

 

模型估计响应的瞬态较少。代价是自旋和自旋速率响应的沉淀时间较长。 

 参考资料

[1] Zhou, Kemin, John Comstock Doyle, and K. Glover. Robust and Optimal Control. Englewood Cliffs, N.J: Prentice Hall, 1996.