矩阵在图形学以及Unity中的应用
自己整理了一下图形学中矩阵的相关内容，算是一个知识摘抄吧，正文如下。
1-矩阵简介
矩阵的定义是由若干行和若干列数排在一起组成的数表。
首先由线性方程组引出矩阵：
其中，方程组的全部系数，未知数，和等式右边的常数分别可以组成一个m＊n，n＊1，n＊1的矩阵，那么上述方程组可以用矩阵的运算来表述为：
更多矩阵的数学方面基础知识在此不多做介绍，可以阅读参考文献2中线性代数的相关知识。
2-矩阵在坐标系转换中的应用
在3D图形学中，一个点的坐标或者一个平面的法向量都可以用一个3维向量来表示，所以在图形学中，可以用下面的线性变换方程组表示矩阵在坐标转换过程中的作用：
可以发现向量
是由向量
在矩阵
的作用下变换而成，用公式表示就是：
在图形学中，为了将一个顶点渲染到任意方向，任意位置的摄像机中，必须将物体的所有定点从物体坐标系变换到世界坐标系，接着再从世界坐标系变换到摄像机坐标系。其中的数学变换总结如下：
由上式可知，只要在渲染循环外将两个转换矩阵的乘积预先计算出来，就可以在渲染时通过一次转换完成从物体坐标到摄像机坐标的转换。
但是使用3*3矩阵转换坐标有一个问题，为了阐述这个问题先引入线性变换和仿射变换的概念。
在数学中，如果一个映射F保持了基本运算：加法和数量乘，那么就可以称该映射为线性的，即：
以及：
所以，上面对于向量
的变换属于线性变换，并且零向量的任意线性变换的结果仍然是零向量，因为：
可以看出，线性变换不会导致平移（原点位置上不会变化）。
仿射变换是指线性变换后接着平移。因此，仿射变换的集合是线性变换的超集，任何线性变换都是仿射变换，但不是所有的仿射变换都是线性变换。因此：
其中G为仿射变换，F为线性变换，b为常量。
因为线性变换无法实现平移，所以在图形学中代表点的坐标的向量都是4D向量，而4D向量和4*4矩阵不过是对3D运算的一种方便的记法而已。
4D向量有4个分量，前三个是标准的x，y和z分量，第四个是w，有时称作齐次坐标。
为了理解首先看一下2D中的齐次坐标，它的形式为
。想象在3D中w＝1处的标准2D平面，实际的2D点
用齐次坐标表示为
，对于那些不再w＝1平面上的点，则将他们投影到w＝1平面上。所以齐次坐标
映射的实际2D点为
。因此给定一个2D点
，齐次空间中有无数多个点与之对应。所有点的形式都为
,k不等于0。这些点构成一条穿过齐次原点的直线。如下图：
当w＝0时，除法未定义，因此不存在实际的2D点。然而，可以将2D齐次点
解释为“位于无穷远的点”，它描述了一个方向而不是一个位置。
4D坐标的基本思想相同。实际的3D点能被认为是在4D中w＝1“平面”上。4D点的形式为
，将4D点投影到这个“平面”上得到相应的实际3D点
。w＝0时4D点表示“无限远点”，它描述了一个方向而不是一个位置。
现在看在4D中如何使用矩阵乘法来表达平移：
设想没有平移的变换后接一个有平移的变换，设R为旋转矩阵（实际上可以是其他的3D线性变换），T为实现4D位移的变换矩阵：
将向量v先旋转再平移，新的向量v’计算如下(注意列向量在右边):
根据矩阵乘法的结合律可以将两个矩阵结合称一个，即：
M的左边3*3部分是旋转部分，最右边一列是平移部分。
接下来看w＝0所表示的“无穷远点”，可以发现若w分量为0，则平移向量
不会起作用。换句话说，4D向量中的w分量能够“开关”4*4矩阵的平移部分。应用此性质可以区分“位置”（如顶点坐标，应该平移）和“方向”（如表面法向量，不应该平移）。从几何意义上来说，能将第一类数据当作“点”，第二类数据当作“向量”。
以上计算中，齐次坐标w分量的值只有0或1，实际上还有其他w值也有意义的4D坐标，更加明确一些，可以利用此性质进行透视投影。
透视投影在图形学中非常重要，因为它是人类视觉系统的模型。
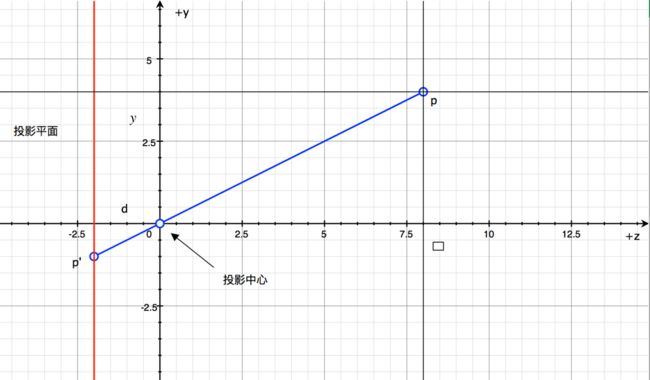
上图所示为从侧面看3D空间中p点以原点为投影中心投影至p’点（原理参考小孔成像）。投影平面为z=-d。现在只需要求出新的y。由相似三角形可得：
类似有：
因此，点p通过原点向平面z=-d投影的结果为：
在实际应用中，负号会带来不必要的复杂性，所以将投影平面移到投影的前面（也就是说，平面z＝d）。
则有：
下面讨论如何使用4*4矩阵进行透视投影。
从4D到3D的变换意味着除法运算，因此可以构造一个4*4矩阵，使得变换后的w为x,y,z的公分母，这里设初始点有w＝1。
先对3D形式表达的p’坐标变形有：
将4D齐次向量变换到3D中时，要用4D向量除以w，反推可知p’的4D形式为:
。
因此需要一个这样的4*4矩阵，可以将
变换为
。
则有：
这样就得到了一个4*4投影矩阵。
3-图形学中多坐标系的概念
多坐标系的概念很多地方都有详细的讨论，这里只是简单介绍一下。
下面是图形流水线中表示物体或者场景的几何数据的一个处理流程。
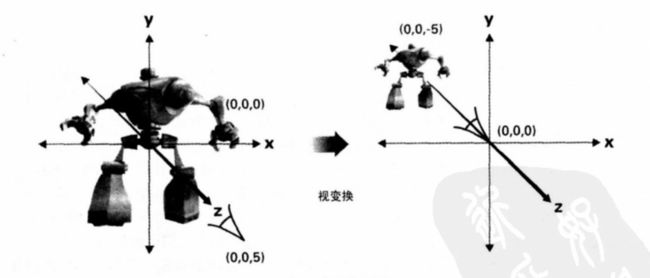
应用程序在物体空间（也称模型空间）里指定顶点位置。这部分一般是由美工在3D建模软件中完成的。例如置顶一个人物模型的脚底平面中心为原点，正面朝向为z轴正向，脚底到头方向为y轴正向，以人物为基准向右为x轴正向。
通常应用程序维护每个物体空间的顶点位置为一个3D向量，每个顶点也许还有一个附随的在物体空间的表面的法向量。
一个物体的物体空间和其他对象没有空间上的关系。世界空间的目的是为在一个场景中的所有物体提供一个绝对的参考（注意这里的“绝对”只是在场景中的“绝对”）。世界空间坐标系的建立可以任意选择。
在物体空间中指定的物体被放置到世界空间的方法要依靠建模变换。例如也许需要旋转，平移和缩放一个椅子的三维模型，以使椅子正确的放在世界空间中，这里放的概念即将模型各顶点在物体空间的坐标通过建模变换变成在世界空间的坐标。
最后，要通过一个特殊的视点（眼睛，摄像机）观看场景，在称为眼睛空间（或视觉空间）的坐标系统里，眼睛位于坐标系统的原点。
从世界空间位置到眼空间位置的变换是视变换，即将世界坐标的原点移至眼睛的位置，z轴正向是视线方向，x轴向右，y轴向上。
大部分的光照和其他着色计算都会涉及位置和表面法向量。通常当它们在眼空间或者物体空间执行时往往更加有效，世界空间在应用程序中为场景里的物体建立总的空间关系时非常有用，但是它对光照和其他着色计算并不特别有效。
因为这个原因，通常把代表建模变换和视变换的矩阵乘在一起组成一个单独的modelview矩阵。
在眼空间之后的坐标系统被称为剪裁空间，在这个空间中的坐标系统被称为剪裁坐标（unity shader中顶点程序输出的顶点位置是在剪裁空间中的）。
从眼空间到剪裁空间的坐标变换被称作投影变换（对应上面2中的投影变换）。对应投影变换的4*4矩阵被称为投影矩阵。
最后需要将齐次形式的剪裁坐标变为一个二维坐标(x,y)和一个深度值。用w除以x,y,z能完成这项工作。生成的结果坐标被称为标准化的设备坐标。
最后一步是将标准化设备坐标转换为使用像素度量x和y的最后的坐标系统。这一步骤叫做视口变换(viewport transform)，它为图形处理器的光栅器提供数据。另一个被称为深度范围变换，缩放顶点的z值到在深度缓冲中使用的深度缓存的范围内。
4-Unity中的常用矩阵
Unity shader中有很多常用矩阵，它们都是由Unity计算出，提供给cg程序使用的。详细可以参照unity官方文档中的Built-in shader variables条目。
这里有一个小问题，我们知道，如果需要将模型坐标变换成眼睛空间中的坐标，需要用顶点坐标乘modelview矩阵，即UNITY_MATRIX_MV。
很明显如果这个变换不是等角变换（即变换前后两向量夹角的大小和方向都不改变，包括平移旋转和均匀缩放），那么原本垂直于平面的法向量与平面之间的夹角就会改变，不再是垂直关系（这里的平面即三点确定的一个平面，为了理解方便可以考虑2D情况即两个点确定的一个向量，若原本法向量与两点确定的向量夹角为90度，经过非等角变换后这两个向量之间夹角可能不再是90度）。
使用modelview矩阵的逆转置矩阵而不是modelview矩阵本身乘法向量可以解决这个问题。证明如下，假设可以保持垂直关系的矩阵为T，平面的任意向量为p，movelview矩阵为M，法向量为n。
则有:
很明显，若 
（I为单位矩阵），则满足上式，故若：
就可以保证在变换后两个向量仍然垂直。注意这里只是利用了T和M互为逆转置是可以保证两个向量在变换后仍然垂直的充分条件这一性质，并不是说若变换后两个向量垂直那么两个矩阵一定互为逆转置（注意充分性和必要性的区别）。
所以，法向量只需乘modelview的逆转置矩阵UNITY_MATRIX_IT_MV,就可以保证变换后法向量仍然垂直于平面。
个人整理，有错误还请指出。
参考文献：
《3D数学基础：图形与游戏开发》
《工程数学－线性代数同济第六版》
《Cg教程：可编程实时图形权威指南》