【算法小记】深度学习——循环神经网络相关原理与RNN、LSTM算法的使用
文中程序以Tensorflow-2.6.0为例
部分概念包含笔者个人理解,如有遗漏或错误,欢迎评论或私信指正。
卷积神经网络在图像领域取得了良好的效果,卷积核凭借优秀的特征提取能力通过深层的卷积操作可是实现对矩形张量的复杂计算处理。但是生活中除了图像这样天然以矩阵形式存储的数据以外,还有众多以时间轴方向的连续数据。例如传感器的采集的复合数据,某个事件的历史发展数据等。同时我们日常生活中无时无刻存在的自然语言也是一个一维连续的数据。
通过上面的引言我们不难发现,一维的时间序列数据、文本信息相比图像本身数据的结构有着较大的差距。图像数据是一个矩形的矩阵形式,时间轴和文本数据是一个一维的列表数据。卷积网络通常在处理矩阵结构的数据时具有较好的效果,面对狭长的时间轴数据卷积难以发挥特征提取的功效。为了适应这样的数据结构,人们进一步参考人类的认识过程,发明了循环神经网络结构RNN。

循化神经网络整体的工作原理同样没有脱离基础的神经网络构建流程,主要由以下几个流程构成:
数据处理> 网络构建> 设置训练参数> 前向传播> 计算损失> 梯度下降更新参数> 迭代完成> 导出模型> 预测
不同于全连接神经网络和卷积神经网络,RNN中不使用简单的ML神经元模型也不使用卷积运算来提取特征,而是设计了一个新的循环核来提取连续数据的特征,也可以理解为一种新的神经元模型。
循环神经网络
通过上文的简介,我们针对时间轴序列数据的特征提取,可以提出以下几个问题:
- 得到的数据与时间相关,如何让神经元提取的特征保留时间的前后信息?
- 一段序列数据是一个整体,前后关联,训练时数据应该怎样怎样输入?是一次性全部输入?
- 假如有一个神经元可以提取时间维度上的特征,那怎样才能让处理连续数据的神经元构建一个代码上可用的神经络层?
- 对这样的神经元输入输出以及网络测试时数据的结构应该是什么样子?
现在有了这些问题我们再去理解循环神经网络就会发现很多细节的问题就迎刃而解了。
循环核
首先我们需要设计一个神经元模型可以学习到数据的前后关系。回想控制系统中如何发现数据的上下文关系?使用反馈网络加时滞环节,时滞环节能够获得之前一定时间点的数据,加上反馈环节后就可以让当前输入的信号和之前的信号进行结合计算了。换句话说就是要想办法保留下上一个时间的数据来参加当前时间数据的处理。我们先看一下再控制系统中,如果用一个时滞环节加上反馈来计算每个时间的输出,结构可以是这样:

通过这附图可以看出时滞环节采集了上一个时间段的数据,并且反馈到了当前时间段的输入上,所以这个模型可以在一定程度上记住输入数据的时间特征。那同样的可以在神经元中设计能保留上一个时间点的数据,并且能够和当前时间点的数据结合,再设计一定的输入输出结构,那么神经元就可以实现对时间数据的保留了。
在循环核的定义中有如下结构:

网络有一个输入一个输出,输入经过第一个输入卷积核Wxh计算后和反馈Wh相加后存储到循环核ht中,然后输出数据是存储的ht和输出卷积核Why计算的结果。每一个时间的数据输入之后都会存储下来用于下一次的计算。整个计算过程作者的论文中已经说明。网络在反向传播时更新的参数就是Wxh、Why、Whh三个卷积矩阵的参数以及输入和输出的偏置项b。最终循环核的输出yt还会经过一次softmax计算,以概率输出可能情况。

在RNN的论文中,作者通过对循环时间核结构的优化进一步的完善了长时间序列数据的预测。一个循环核可以处理输入的一个时间点数据,那假如我们有N个时间长度的数据,那就把N个循环核首尾连接,这样对于每一个循环核其输入都是当前时间输入和历史数据共同作用的结果。

首尾连接后,可以选择每个循环核的输出都是有效数据,也可以选择只有最后一个循环核的输出是有效数据。通常前者被用来做长时间序列数据的处理(连续输入-连续输出),后者被用来做本文续写和生成式算法(连续输入-节点输出)。
理解循环核存储数据的作用和首尾相连的结构是学习RNN中最重要的一环。
循环核时间展开步
理解了循环核的概念后,当我们把循环核首尾相连后,输入数据的长度(一次输入多长时间的数据)也是十分重要的。就比如人们说话时一句话实际上是有长度限制的,没有人能一口气说无限长的句子。对于循环神经网络来说,展开步的步长就等于网络一次能听到的句子长度。再比如有一个传感器检测系统,我们通常只观测它在一个时间段t内的数据趋势,那么就可以按照t长度采样足够多组的数据,一次送入一组数据,然后循环迭代不同组的数据完成网络的训练。在下面的图片中假如有t个时间点的数据,那么循环网络的时间步就是t。

到这里我们已经解决了让神经元提取的特征保留时间的前后信息,训练时数据应该怎样怎样输入这两个问题。
循环计算层
在实际应用中,对一个时间点数据我们可能不会只使用一个循环核,而是使用多个循环神经核串联计算一个时间点的数据然后根据需要来判断它如何输出。在构建时就可以把这样的一组神经元封装为一个网络层。

通过多个层的串联就最终实现了循环核的复合串联,即学习了某个时刻的数据,也充分学习了整个维度上的数据。
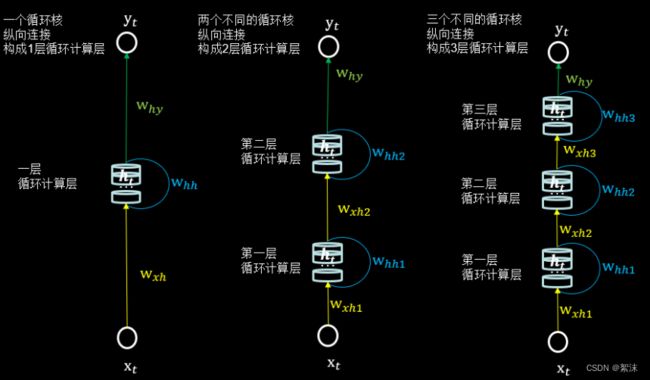
在上图中从左到右以此是由1个、2个、3个循环核构成的循环神经网络层。
TF中的循环计算层API
前面已经说过,当得到的前向传播结果之后,RNN和其他神经网络类似,通过定义损失函数,使用反向传播梯度下降算法训练模型。RNN 唯一的区别在于:由于它每个时刻的节点都可能有一个输出,所以 RNN 的总损失为所有时刻(或部分时刻)上的损失
和。不过这点tf中的keras已经帮我们封装好了。
tf.keras.layers.SimpleRNN(神经元个数,activation=‘激活函数’,return_sequences=是否每个时刻输出ℎ到下一层)
其中的主要参数有:第一个参数是输入神经元的个数
activation:选择激活函数,由于循环核的计算特性一般均使用“tanh”激活函数
return_sequences:是一个bool型变量,为True时每个循环核的输出都是有效数据,为false时只有最后一个神经元的输出是有效数据。分别对应了序列输入序列输出,序列输入单个输出。如果使用True时,后面通常会跟上全连接Dense层,用于网络数据的输出。
值得注意的是,由于循环核的特殊结构,输入API的数据应该是三维的张量,由【输入样本数,循环核展开步数,每个时间步输入的特征个数】组成。输出数据的格式:当return_sequences为True时输出是二维张量,结构为【输入样本数,本层神经元的个数】,当return_sequences为false时输出是三维张量,结构为【输入样本数,循环核时间展开步,本层神经元个数】
计算流程
首先我们应该记住循环核的结构。那么假设我们现在有两个数据Xt和X(t+1),可以推出单个循环核的计算流程如下:
输入数据后循环核中存储的数据为: h t = t a n h ( x t ⋅ w h x + h t − 1 ⋅ w h h + b h ) h_t = tanh( x_t \cdot w_{hx} + h_{t-1} \cdot w_{hh} + b_h ) ht=tanh(xt⋅whx+ht−1⋅whh+bh) 输入数据 x t \ x_t xt 乘以输入卷积核 w h x \ w_{hx} whx 加上上一次存储的数据 h t − 1 \ h_{t-1} ht−1 乘以历史卷积核 w h h \ w_{hh} whh ,在加上偏置 b h \ b_h bh ,最后经过tanh激活函数得到当前输入的 h t \ h_t ht。在经过当前输入 h t \ h_t ht的输出计算: y t = s o f t m a x ( h t ⋅ w h y + b y ) y_t = softmax( h_t \cdot w_{hy}+b_{y}) yt=softmax(ht⋅why+by) 当前的 h t \ h_t ht 乘以输出卷积核 w h y \ w_{hy} why再加上输出偏置 b y \ b_y by 就得到了当前循环核的输出。上面描述的是单个循环核的计算流程,也如下图所示:

当多个循环核连接在一起时将串联计算:

当输入了很长的连续数据时,假设循环核是两个串联,每个节点都输出数据,那计算结构是:

理解了上面这幅图的结构,那恭喜你已经基本掌握了循环神经网络计算的要点。
RNN应用实例
这里我们通过一个简单的字符串序列来演示循环神经网络的构建过程。
首先我们定义任务为:
| 输入字母 | 输出字母 |
|---|---|
| “abcd” | “e” |
| “bcde” | “a” |
| “cdea” | “b” |
| “deab” | “c” |
| “eabc” | “d” |
那么可以定义数据结构为:
import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import Dense, SimpleRNN
import matplotlib.pyplot as plt
import os
input_word = "abcde"
w_to_id = {'a': 0, 'b': 1, 'c': 2, 'd': 3, 'e': 4} # 单词映射到数值id的词典
id_to_onehot = {0: [1., 0., 0., 0., 0.], 1: [0., 1., 0., 0., 0.], 2: [0., 0., 1., 0., 0.], 3: [0., 0., 0., 1., 0.],
4: [0., 0., 0., 0., 1.]} # id编码为one-hot
x_train = [ # 特征数据,长度是4
[id_to_onehot[w_to_id['a']], id_to_onehot[w_to_id['b']], id_to_onehot[w_to_id['c']], id_to_onehot[w_to_id['d']]],
[id_to_onehot[w_to_id['b']], id_to_onehot[w_to_id['c']], id_to_onehot[w_to_id['d']], id_to_onehot[w_to_id['e']]],
[id_to_onehot[w_to_id['c']], id_to_onehot[w_to_id['d']], id_to_onehot[w_to_id['e']], id_to_onehot[w_to_id['a']]],
[id_to_onehot[w_to_id['d']], id_to_onehot[w_to_id['e']], id_to_onehot[w_to_id['a']], id_to_onehot[w_to_id['b']]],
[id_to_onehot[w_to_id['e']], id_to_onehot[w_to_id['a']], id_to_onehot[w_to_id['b']], id_to_onehot[w_to_id['c']]],
]
y_train = [w_to_id['e'], w_to_id['a'], w_to_id['b'], w_to_id['c'], w_to_id['d']] # 输出长度是1
np.random.seed(7)
np.random.shuffle(x_train)
np.random.seed(7)
np.random.shuffle(y_train)
tf.random.set_seed(7)
紧接着定义网络和网络参数,同时在这一步中定义了循环神经网络,循环核深度为3(3个串联),在不定义return_sequences时默认是True。输出数据在经过一次全连接,使用softmax输出,通过查询输出张量中概率最大的值作为最后的输出。
# 使x_train符合SimpleRNN输入要求:[送入样本数, 循环核时间展开步数, 每个时间步输入特征个数]。
# 此处整个数据集送入,送入样本数为len(x_train);输入4个字母出结果,循环核时间展开步数为4; 表示为独热码有5个输入特征,每个时间步输入特征个数为5
x_train = np.reshape(x_train, (len(x_train), 4, 5))
y_train = np.array(y_train)
model = tf.keras.Sequential([
SimpleRNN(3),
Dense(5, activation='softmax')
])
model.compile(optimizer=tf.keras.optimizers.Adam(0.01),
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
metrics=['sparse_categorical_accuracy'])
最后开始训练:
cp_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_save_path,
save_weights_only=True,
save_best_only=True,
monitor='loss') # 由于fit没有给出测试集,不计算测试集准确率,根据loss,保存最优模型
history = model.fit(x_train, y_train, batch_size=32, epochs=100, callbacks=[cp_callback])
model.summary()
前向推理测试:
preNum = int(input("input the number of test alphabet:"))
for i in range(preNum):
alphabet1 = input("input test alphabet:")
alphabet = [id_to_onehot[w_to_id[a]] for a in alphabet1]
# 使alphabet符合SimpleRNN输入要求:[送入样本数, 循环核时间展开步数, 每个时间步输入特征个数]。此处验证效果送入了1个样本,送入样本数为1;输入4个字母出结果,所以循环核时间展开步数为4; 表示为独热码有5个输入特征,每个时间步输入特征个数为5
alphabet = np.reshape(alphabet, (1, 4, 5))
result = model.predict([alphabet])
pred = tf.argmax(result, axis=1)
pred = int(pred)
tf.print(alphabet1 + '->' + input_word[pred]) # 找到输出的最大值
LSTM
在上面RNN的介绍和数据中不难发现输入数据的尺度会直接影响到循环核的个数和循环步数。假如需要输入的数据长度长度足够长的时候,再使用RNN构建网络会让网络的输入尺寸过大,在很大的尺度上训练数据可能会出现梯度消失的问题,所以RNN在面对太长的数据时很难发挥出好的效果。
思考导致这个问题的原因,主要有:RNN的循环核只存储上一次的数据(对历史数据的记忆能力不够),每个输入都直接经过激活函数计算(数据长度太大时累加的激活函数计算会让最后梯度消失)。那为了解决这两个问题LSTM应运而生。
LSTM循环核结构
在LSTM的循环核中添加了几个门模块,分别是输入门it,遗忘门ft,输出门ot,以及表达长期记忆的细胞态Ct,等待长期记忆形成的候选态C’t。


可以看到网络的结构:

直接看原文的公式确实有些抽象,那怎样去形象一些的理解呢?
相当于在原来RNN循环核的基础上,再一次添加上5个元素:在输入位置添加输入门,他会按照设置的比例限制输入的数据中有多少能被用来计算;在遗忘门的位置会按照设置的比例选择有多少数据被遗忘;输出门则是按照设置的参数输出有效的数据;在原有的记忆体ht基础上添加了新的长期记忆细胞态 C t \ C_t Ct来记忆上一个时刻遗忘门输出和当前时刻新知识的和;最后还添加了当前时刻的新知识 C ~ t \ \tilde{C}_t C~t 他是当前时刻输出数据和上个时刻短期记忆ht的函数。这样说可能还是有些抽象,那我们再一步一步的使用函数来描述LSTM中的计算流程:
1、当前状态的下的短期记忆取决于当前输入和历史的长期记忆: h t = o t ∗ t a n h ( C t ) h_t=o_t\ast tanh(C_t) ht=ot∗tanh(Ct) 2、当前时刻的长期记忆取决于上一个时刻的长期记忆通过遗忘门的输出和当前时刻的新记忆: C ~ t = t a n h ( W c ⋅ [ h t − 1 , x t ] + b c ) \tilde{C}_t=tanh(W_c \cdot [h_{t-1},x_t]+b_c) C~t=tanh(Wc⋅[ht−1,xt]+bc) 3、当前时刻的新记忆取决于当前时刻的输入和上一个时刻的短期记忆: C t = f t ∗ C t − 1 + i t ∗ C ~ t C_t=f_t\ast C_{t-1} + i_t\ast \tilde{C}_t Ct=ft∗Ct−1+it∗C~t 4、最终输出的数据是当前时刻的长期记忆经过遗忘门后的输出: o t = σ ( W o ⋅ [ h t − 1 + b o ] ) o_t = \sigma (W_o\cdot[h_{t-1}+b_o]) ot=σ(Wo⋅[ht−1+bo]) 同时每个门的输出都是经过sigmoid函数进行了归一化的结果。通过这样的门结构和长短期记忆组合最终实现了LSTM对长数据序列的处理和计算。
LSTM的tf-API
在tf.keras中提供了LSTM的API,其输入参数基本和输入的数据结构基本上与上文中RNN的输入结构相同,这里不做重复。我们直接看一个计算的例子:
model = tf.keras.Sequential([
LSTM(80, return_sequences=True),
Dropout(0.2),
LSTM(100),
Dropout(0.2),
Dense(1)
])
在这个例子中定义了两个LSTM层,并且每个LSTM循环核都输出有效数据,层的输出经过20%的Dropout避免网络过渡拟合。最后用一个1输出的全连接层来输出预测的结果。
由于代码量较长,这里就不重复给出LSTM的预测代码。但是LSTM的基本形式和RNN预测相同,不过LSTM对长时间序列的处理能力就更上一层楼。