树 -- 二叉查找树

二叉查找树

---

 

　　二叉查找树的的定义为：对于一个树中的任意一个非空节点，其左子节点树中的键值都不大于它，其右子节点树中的键值都不小于它。那么这棵树就是二叉查找树。

　　“In computer science, a search tree is a tree data structure used for locating specific values from within a set. In order for a tree to function as a search tree, the key for each node must be greater than any keys in subtrees on the left and less than any keys in subtrees on the right.” -- Wikipedia

　　因为二叉查找树这样的性质，所以能够通过比较目标值与当前节点的值来逐步定位包含目标值的节点。这个定位过程就是“查找”操作中的一种 --- 查找目标节点。因为二叉查找树的是通过比较来定位数据，所以在二叉查找树上进行“查找”操作的时间复杂度与树的深度有关。同样，“删除”、“添加”操作也与树的深度有关。

　　对于一棵n个节点的完全平衡二叉查找树，进行一次"查找"操作所需的时间复杂度为O(lgⁿ)；对于退化为链表的二叉查找树，时间复杂度为O(n)。也就是讲，二叉查找树显得越“平衡”，所需的时间就越短。在下个笔记中，会探讨保持二叉查找树的“平衡性”的方法。本次主要着眼于二叉查找树的基本操作。

　　

遍历

---

 

　　对一个二叉查找树进行中序遍历所得的序列为非递减序列。（通过在递归遍历中记录上个节点的值，可以判断某个树是否为二叉查找树。）

　　定理：如果x是包含n个节点的树的跟，对其调用中序遍历方法的时间复杂度为O（n）。

　　证明: 算导.替代法证明. T(n) = (c+d)n + c.

 

　　问题(1):二叉查找树与最小堆之间的区别?能否利用最小堆在O(n)时间内按序输出含有n个节点的树中关键字?

　　　　解答:在最小堆中,除了根节点之外的每个节点都有,Key[parent[i]] <= Key[i],既节点的值小于左右子树中节点的值.而在二叉查找树中,Key[i] >= Key[left[i]] && Key[i] <= Key[right[i]].

　　　　最小堆的性质对与按序打印的辅助力度远没有二叉搜索树大.因为某个节点的后继节点可能极可能存在与左子树中,也可能存在于右子树中.

我们知道建造一颗最小堆需要耗时O(n),但是排序过程中的比较要话费Ω(nlgn),所以不存在O(n)时间内的最小堆按序输出算法.[Wait to be more specific !]

　　

查询

---

　　(1)查找给定元素

　　　　对于一颗高度为h的二叉查找树,查询一次的时间复杂度为O(h).

 1 template<class T>

 2 TRNode<T>* sTree<T>::search(T val)const {

 3     TRNode<T> *curr = root;

 4 

 5     while(curr!=nil){

 6         if(curr->val == val){

 7             return curr;

 8         }else if(curr->val > val){

 9             curr = curr->leftChild;

10         }else{

11             curr = curr->rightChild;

12         }

13     }

14 

15     return nil;

16 }

　　(2)查找最大关键字

　　　　因为对于二叉查找树中的任一节点,左子树中的节点键值都不大于它,右子树中节点的键值都不小于它.因此,对最大元素的查找就是从根节点开始,不断查找右子节点的过程.

1 template<class T>

2 TRNode<T>* sTree<T>::maximum() const{

3     TRNode<T> *curr = root;

4     while(curr!=nil && curr->rightChild!=nil){

5         curr = curr->rightChild;

6     }

7 

8     return nil;

9 }

　　(3)查找最小关键字

　　　　同(2),是不断查询左子节点的过程.

1 template<class T>

2 TRNode<T>* sTree<T>::minimum() const{

3     TRNode<T> *curr = root;

4     while(curr!=nil && curr->leftChild!=nil){

5         curr = curr->leftChild;

6     }

7 

8     return nil;

9 }

　　(4)查找某节点的前驱

　　　　对于某一个节点,其右子树的值都不小于它,所以不可能存在其前驱节点;左子树中的值都不大于它,因此会存在前驱节点.

　　　　此外,还要考虑其父节点们,如果它是父节点的左子节点,在父节点的值不小于它,但是如果其父节点是祖父节点的右儿子,此时祖父节点不大于它,有可能是其后继.(祖父节点只是个特例,还可以继续向上判读更高层的祖先节点!)当左子树和满足条件的祖先节点都存在时,左子树优先.

 1 template<class T>

 2 TRNode<T>* sTree<T>::predecessor(TRNode<T>* x) const{

 3     if(x->leftChild != nil){

 4         TRNode<T> *curr = x->leftChild;

 5         while(curr!=nil && curr->rightChild!=nil)

 6             curr = curr->rightChild;

 7 

 8         return curr;

 9     }

10 

11     TRNode<T> *parent = x->parent;

12     if((parent = x->parent)!=nil && parent->leftChild == x){

13         x = parent;

14     }

15 

16     return (parent==nil)?nil:parent;

17 }

　　(5)查找某节点的后继

　　　　分析同(4).

 1 template<class T>

 2 TRNode<T>* sTree<T>::successor(TRNode<T>* x)const{

 3     if(x->rightChild != nil){

 4         TRNode<T> *curr = x->rightChild;

 5         while(curr != nil && curr->leftChild != nil){

 6             curr = curr->leftChild;

 7         }

 8         return curr;

 9     }

10 

11     TRNode<T> *parent = x->parent;

12     while((parent!=nil) && (parent->rightChild!=nil)){

13         x = parent;

14     }

15 

16     return (parent==nil)?nil:parent;

17 }

　　

　　重要性质:如果二叉树中某个节点有两个儿子,则其前驱节点没有右儿子,后继节点没有左儿子.

 

插入

---

　　　通过从根到叶子的比较,可以将某个节点添加到二叉查找树.这个动作可能会是的查找树变得不"平衡",我们在之后的讨论中会涉及到平衡性的"恢复"方法.在这里只考虑插入的过程.

　　　插入过程与查找特定元素的过程十分类似.

template<class T>

void sTree<T>::insert(T val){

    TRNode<T> *curr = root;

    TRNode<T> *parent = nil;

    while(curr!=nil){

        parent = curr;

        if(curr->val > val){

            curr = curr->leftChild;

        }else{

            curr = curr->rightChild;

        }

    }//在树中定位合适的位置



    TRNode<T> *dest = new TRNode<T>(val,nil,nil,nil);

    if(parent == nil){//This represents root == nil

        root = dest;

        dest->parent = dest->leftChild = dest->rightChild = nil;

    }else{

        if(parent->val > val){

            parent->leftChild = dest;

        }else{

            parent->rightChild = dest;

        }



        dest->parent = parent;

    }//插入新节点

}

 

删除

---

　　在删除操作中,难点是我们需要保证删除操作之后,二叉搜索树仍然能保持性质.

　　考虑以下三种情况:

　　case 1:要删除的节点没有子节点.此时,直接可以直接将其移除,不会影响二叉搜索树的性质;

　　

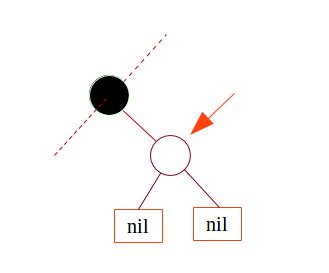
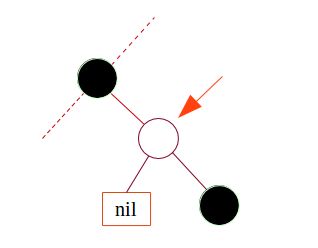
　　case 2:要删除的节点只有左子节点或右子节点.此时,将其仅有的子节点连接到其父节点,可以保持二叉搜索树的性质;

　　

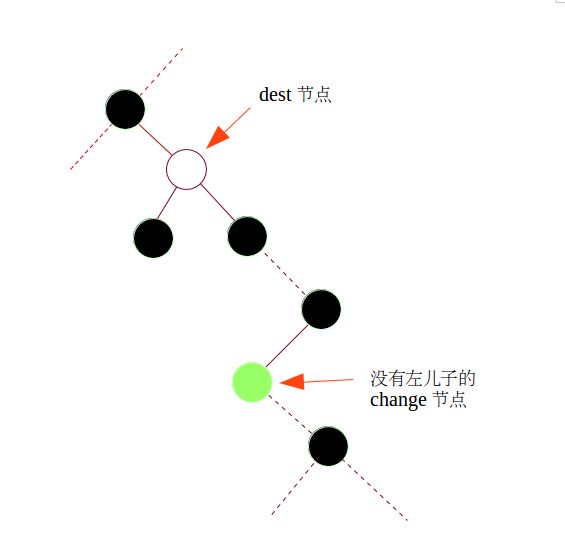
　　case 3:要删除的节点既有左子节点又有右子节点.此时,通过查找章节的"重要性质"我们可以指导,其后继节点没有左子树 ! 如果我们将后继节点自身的右子树与后继节点的父亲相连,之后用后继节点来代替本节点,二叉树的性质仍然能够得到保持.

　　

TRNode<T>* sTree<T>::erase(T val){

    TRNode<T> *dest = search_iteration(val);//定位目标节点



    if(dest != nil){

        TRNode<T> *change;//我们会在树中选择合适的节点来删除掉

        if(dest->leftChild==nil || dest->rightChild==nil){

            change = dest;//选择目标节点本身

        }else{

            change = successor(dest);//选择其后继节点坐为要删除的节点

        }



        TRNode<T> *child;//获取要删除节点的唯一的子节点

        if(change->leftChild == nil){

            child = change->rightChild;

        }else{

            child = change->leftChild;

        }

        TRNode<T> *parent = change->parent;

        child->parent = change->parent;

        if(change == parent->leftChild){

            parent->leftChild = child;

        }else{

            parent->rightChild = child;

        }//将父节点与子节点连接



        if(change != dest){//Copy content except for pointer

            dest->val = change->val;

        }//如果要删除的节点时后继节点时,复制数据到目标节点



        delete change;

    }



    return dest;

}

 

　　问题:可以这样对n个树进行排序:先构造一颗包含这些树的二叉查找树(重复应用insert来逐个插入这些数),然后按照中序遍历来输出.这个排序算法的最好和最坏情况是什么?

　　解答:这个算法可以表示如下:

　　　　 for(int i=0;i<n;i++)

　　　　　　insert(val[i]);

　　　　inorder();

 

　　　　最坏的情况为Θ(n²):这发生在待处理序列有序的情况下,执行insert操作的时间复杂度总共为Θ(n²).

　　　　最好的情况为Θ(nlgn):这发生在执行insert操作后产生一颗Θ(lgn)的二叉树时. 

　　

参考

---

　　算法导论　　

　　Solutions to exercises and problems