bzoj1179
其实是最大团问题,但是直接dfs不保证不tle
题解再次来自lsj(懒得敲):
对于一个强连通分量, 一定是整个走或者不走, 所以tarjan缩点然后跑dijkstra或spfa
spfa

1 #include<bits/stdc++.h> 2 #define clr(a,x) memset(a,x,sizeof(a)) 3 #define rep(i,l,r) for(int i=l;i<r;i++) 4 #define Rep(i,a) rep(i,0,e[a].size()) 5 #define REP(i,a) rep(i,0,e1[a].size()) 6 typedef long long ll; 7 using namespace std; 8 int read() 9 { 10 char c=getchar(); 11 int ans=0,f=1; 12 while(!isdigit(c)){ 13 if(c=='-') f=-1; 14 c=getchar(); 15 } 16 while(isdigit(c)){ 17 ans=ans*10+c-'0'; 18 c=getchar(); 19 } 20 return ans*f; 21 } 22 const int maxn=500005,inf=0x7fffffff; 23 bool b[maxn],p[maxn]; 24 int dfstime,cnt,s,k,n,m,w[maxn],low[maxn],pre[maxn],scc[maxn],d[maxn],v[maxn]; 25 stack<int>S; 26 queue<int>Q; 27 vector<int>e[maxn]; 28 vector<int>e1[maxn]; 29 void dfs(int a) 30 { 31 low[a]=pre[a]=++dfstime; 32 S.push(a); 33 Rep(i,a){ 34 if(!pre[e[a][i]]){ 35 dfs(e[a][i]); 36 low[a]=min(low[a],low[e[a][i]]); 37 }else if(!scc[e[a][i]]){ 38 low[a]=min(low[a],pre[e[a][i]]); 39 } 40 } 41 if(low[a]==pre[a]){ 42 ++cnt; 43 int x=0; 44 while(x!=a){ 45 x=S.top(); 46 S.pop(); 47 scc[x]=cnt; 48 w[cnt]+=v[x]; 49 b[cnt]|=p[x]; 50 } 51 } 52 } 53 void spfa() 54 { 55 clr(d,0); 56 d[scc[s]]=w[scc[s]]; 57 Q.push(scc[s]); 58 while(!Q.empty()){ 59 int now=Q.front(); 60 Q.pop(); 61 REP(i,now){ 62 if(d[e1[now][i]]<d[now]+w[e1[now][i]]){ 63 d[e1[now][i]]=d[now]+w[e1[now][i]]; 64 Q.push(e1[now][i]); 65 } 66 } 67 } 68 } 69 int main() 70 { 71 n=read(),m=read(),cnt=dfstime=0,clr(low,0),clr(pre,0),clr(scc,0),clr(b,0),clr(p,0); 72 rep(i,0,m){ 73 int from=read(),to=read(); 74 e[from].push_back(to); 75 } 76 rep(i,1,n+1) v[i]=read(); 77 s=read(),k=read(); 78 while(k--){ 79 int t=read(); 80 p[t]=1; 81 } 82 rep(i,1,n+1){ 83 if(!scc[i]) dfs(i); 84 } 85 86 rep(i,1,n+1){ 87 Rep(j,i){ 88 if(scc[i]!=scc[e[i][j]]) 89 e1[scc[i]].push_back(scc[e[i][j]]); 90 } 91 } 92 spfa(); 93 int ans=0; 94 rep(i,1,cnt+1){ 95 if(b[i]) ans=max(ans,d[i]); 96 } 97 printf("%d\n",ans); 98 return 0; 99 }
dijkstra

1 #include<bits/stdc++.h> 2 #define clr(a,x) memset(a,x,sizeof(a)) 3 #define rep(i,l,r) for(int i=l;i<r;i++) 4 #define Rep(i,a) rep(i,0,e[a].size()) 5 #define REP(i,a) rep(i,0,e1[a].size()) 6 typedef long long ll; 7 using namespace std; 8 int read() 9 { 10 char c=getchar(); 11 int ans=0,f=1; 12 while(!isdigit(c)){ 13 if(c=='-') f=-1; 14 c=getchar(); 15 } 16 while(isdigit(c)){ 17 ans=ans*10+c-'0'; 18 c=getchar(); 19 } 20 return ans*f; 21 } 22 struct node{ 23 int d,num; 24 inline bool operator <(const node&A)const{ 25 return d>A.d; 26 } 27 }; 28 const int maxn=500005,inf=0x7fffffff; 29 bool b[maxn],p[maxn]; 30 int dfstime,cnt,s,k,n,m,w[maxn],low[maxn],pre[maxn],scc[maxn],d[maxn],v[maxn]; 31 stack<int>S; 32 vector<int>e[maxn]; 33 vector<int>e1[maxn]; 34 priority_queue<node>Q; 35 void dfs(int a) 36 { 37 low[a]=pre[a]=++dfstime; 38 S.push(a); 39 Rep(i,a){ 40 if(!pre[e[a][i]]){ 41 dfs(e[a][i]); 42 low[a]=min(low[a],low[e[a][i]]); 43 }else if(!scc[e[a][i]]){ 44 low[a]=min(low[a],pre[e[a][i]]); 45 } 46 } 47 if(low[a]==pre[a]){ 48 ++cnt; 49 int x=0; 50 while(x!=a){ 51 x=S.top(); 52 S.pop(); 53 scc[x]=cnt; 54 w[cnt]+=v[x]; 55 b[cnt]|=p[x]; 56 } 57 } 58 } 59 void dijkstra() 60 { 61 clr(d,0); 62 d[scc[s]]=w[scc[s]]; 63 node start; 64 start.num=scc[s],start.d=w[scc[s]]; 65 Q.push(start); 66 while(!Q.empty()){ 67 node now=Q.top(); 68 Q.pop(); 69 if(now.d==d[now.num]){ 70 REP(i,now.num){ 71 if(d[now.num]+w[e1[now.num][i]]>d[e1[now.num][i]]){ 72 d[e1[now.num][i]]=d[now.num]+w[e1[now.num][i]]; 73 node next; 74 next.d=d[e1[now.num][i]]; 75 next.num=e1[now.num][i]; 76 Q.push(next); 77 } 78 } 79 } 80 } 81 } 82 int main() 83 { 84 n=read(),m=read(),cnt=dfstime=0,clr(low,0),clr(pre,0),clr(scc,0),clr(b,0),clr(p,0); 85 rep(i,0,m){ 86 int from=read(),to=read(); 87 e[from].push_back(to); 88 } 89 rep(i,1,n+1) v[i]=read(); 90 s=read(),k=read(); 91 while(k--){ 92 int t=read(); 93 p[t]=1; 94 } 95 rep(i,1,n+1){ 96 if(!scc[i]) dfs(i); 97 } 98 rep(i,1,n+1){ 99 Rep(j,i){ 100 if(scc[i]!=scc[e[i][j]]) 101 e1[scc[i]].push_back(scc[e[i][j]]); 102 } 103 } 104 dijkstra(); 105 int ans=0; 106 rep(i,1,n+1){ 107 if(b[i]) ans=max(ans,d[i]); 108 } 109 printf("%d\n",ans); 110 return 0; 111 }
1179: [Apio2009]Atm
Time Limit: 15 Sec Memory Limit: 162 MBSubmit: 1921 Solved: 763
[Submit][Status][Discuss]
Description
Input
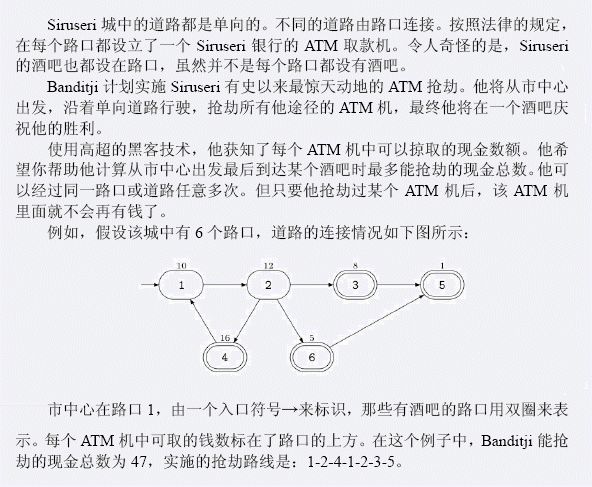
第一行包含两个整数N、M。N表示路口的个数,M表示道路条数。接下来M行,每行两个整数,这两个整数都在1到N之间,第i+1行的两个整数表示第i条道路的起点和终点的路口编号。接下来N行,每行一个整数,按顺序表示每个路口处的ATM机中的钱数。接下来一行包含两个整数S、P,S表示市中心的编号,也就是出发的路口。P表示酒吧数目。接下来的一行中有P个整数,表示P个有酒吧的路口的编号
Output
输出一个整数,表示Banditji从市中心开始到某个酒吧结束所能抢劫的最多的现金总数。
Sample Input
6 7
1 2
2 3
3 5
2 4
4 1
2 6
6 5
10
12
8
16
1 5
1 4
4
3
5
6
1 2
2 3
3 5
2 4
4 1
2 6
6 5
10
12
8
16
1 5
1 4
4
3
5
6
Sample Output
47
HINT
50%的输入保证N, M<=3000。所有的输入保证N, M<=500000。每个ATM机中可取的钱数为一个非负整数且不超过4000。输入数据保证你可以从市中心沿着Siruseri的单向的道路到达其中的至少一个酒吧。
