POJ 3159 Candies 解题报告(差分约束 Dijkstra+优先队列 SPFA+栈)
原题地址:http://poj.org/problem?id=3159
题意大概是班长发糖果,班里面有不良风气,A希望B的糖果不比自己多C个。班长要满足小朋友的需求,而且要让自己的糖果比snoopy的尽量多。
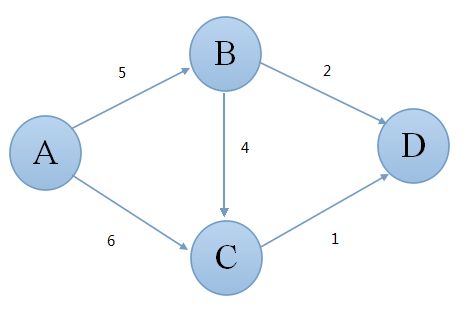
比如现在ABCD四个小朋友,B的糖果不能超过A的5个,如果A的史努比,D是班长,那么班长最多比史努比多7个糖果,而不是5+4+1=9个。
因为如果是9个,就不满足D-A<=(D-C)+(C-A)<=7的条件。
不懂的可以翻一下算法导论,上面有差分约束的定义和证明,总之这是一个求最短路的问题==。
其实为了理解题意,我也花了很久时间SF-_-。
知道是求最短路之后,做法就有很多了,BUT数据量较大,很多做法会超时。这里推荐两个算法,一个是优先队列优化的Dijkstra算法,AC代码如下(579MS):
#include <cstdio> #include <vector> #include <queue> #include <cstring> using namespace std; struct CNode { int k; int w; bool operator<(const CNode& cmp) const { return w>cmp.w; } }; priority_queue<CNode> pq; bool vis[30030]; int first[30030],vv[150010],ww[150010],nxt[150010]; const int inf=~(1<<31); CNode p,q; int main() { // freopen("in.txt","r",stdin); memset(d,0,sizeof(d)); int e=2; int n,m,u,v,w; scanf("%d%d",&n,&m); for(int i=0;i<m;i++) { scanf("%d%d%d",&u,&v,&w); nxt[e]=first[u],vv[e]=v,ww[e]=w,first[u]=e++; } p.k=1; p.w=0; pq.push(p); while(!pq.empty()) { p=pq.top(); pq.pop(); if(vis[p.k]) continue; vis[p.k]=true; if(p.k==n) break; for(int e=first[p.k];e;e=nxt[e]) if(!vis[vv[e]]) { q.k=vv[e]; q.w=p.w+ww[e]; pq.push(q); } } printf("%d\n",p.w); }
另一个是栈优化的SPFA算法(532MS):
#include <cstdio> #include <vector> #include <queue> #include <cstring> using namespace std; int d[30030]; int stack[30030]; bool vis[30030]; int first[30030],vv[150010],ww[150010],nxt[150010]; const int inf=~(1<<31); int main() { // freopen("in.txt","r",stdin); memset(d,0,sizeof(d)); int e=2; int n,m,u,v,w; scanf("%d%d",&n,&m); for(int i=0;i<m;i++) { scanf("%d%d%d",&u,&v,&w); nxt[e]=first[u],vv[e]=v,ww[e]=w,first[u]=e++; } memset(d,0x7f,sizeof(d)); int top=0; stack[++top]=1; vis[1]=true; d[1]=0; while(top) { int a=stack[top--]; vis[a]=false; for(int e=first[a];e;e=nxt[e]) if(d[vv[e]]>ww[e]+d[a]) { d[vv[e]]=ww[e]+d[a]; if(!vis[vv[e]]) { stack[++top]=vv[e]; vis[vv[e]]=true; } } } printf("%d\n",d[n]); }