一个迷宫问题

问题：通过计算机程序找出一条离开迷宫的路径。

迷宫表示：我们用一个二维数组来表示迷宫，设该二维数组为maze[i][j]，1 <= i <= m并且1 <= j <=p。1表示不能通过的位置，0表示可以从上面通过。

如图所示：

         因为迷宫被表示为一个二维数组，因此无论在任何位置都可以用行数i和列数j来表示。同理当前位置[i][j]的下一个位置也可以用[g][h]来表示。我们首先定义8个方向，分别是N,NE,E,SE,S,SW,W和NW。当前位置与下一步所到的位置关系如图：

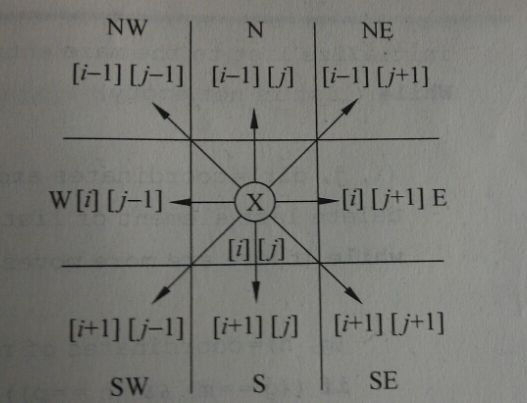
这里必须注意，因为不是所有位置都有8个相邻的位置。如果[i][j]在边界上，无论是i = 1或m，或者j = 1或p，那么相邻位置书都小于8，并且可能只有3个相邻位置存在。为了避免考虑边界条件，我们用1将迷宫包围。这事需要maze[m+2][p+2]来声明迷宫，这里我们假设从maze[1][1]进入，maze[m][p]离开。

另一个化简问题的方法是预先把可能的方向定义在表Move中，如图：

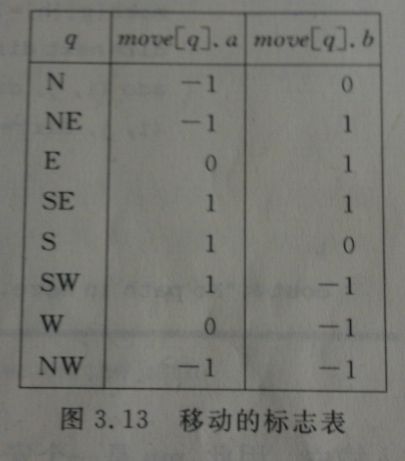
数据结构：

enum directions{N,NE,E,SE,S,SW,W,NW};

class offsets //运动方向的类

{

public:

   int a,b;

};

offsets Move[8];

如果我们当前位置[i][j]，希望下一步在当前位置的东面位置[g][h]，那么进行如下计算：

g = i + Move[E].a;              h = j + Move[E].b;

例如：[3][4]，那么东面一个位置就是[4][4]。

Path分析： 当我们在迷宫中行走的时候，可能有多个方向可以前进。所以每到达一个新位置我们要检查可以行走的方向（即下一步maze[g][h] = 0），并且从东开始顺时针方向一一尝试。因为我们并不能预知那个方向更好，所以只能选择一个方向，并把当前位置和上一步的位置保存起来。这样的话，如果选择了一条错误的路线，就可以退回去并且尝试下一个方向。为了防止进入同一条路径两次，我们使用另一个二维数组mark[m+2][p+2]，该数组中每个元素一开始都被置为0，一旦到达某位置mark[i][j] = 1 。当前进到[m][p]，证明已经找到正确离开迷宫的路径（假设maze[m][p] = 0，否则问题无解）。

代码解决方案：

#include<iostream>
#include<stack>
using namespace std;

const int m = 3;
const int p = 4; 
int maze[m+2][p+2] = {{1,1,1,1,1,1},{1,0,0,1,1,1},{1,1,0,1,1,1},{1,1,1,0,0,1},{1,1,1,1,1,1}};
int mark[m+2][p+2];enum directions{N,NE,E,SE,S,SW,W,NW};

class offsets //运动方向的类
{
public:
　　int a,b;
};
offsets Move[8];
void funtion1()
{//初始化 运动方向
　　Move[N].a = -1;
　　Move[N].b = 0;
　　Move[NE].a = -1;
　　Move[NE].b = 1;
　　Move[E].a = 0;
　　Move[E].b = 1;
　　Move[SE].a = 1;
　　Move[SE].b = 1;
　　Move[S].a = 1;
　　Move[S].b = 0;
　　Move[SW].a = 1;
　　Move[SW].b = -1;
　　Move[W].a = 0;
　　Move[W].b = -1;
　　Move[NW].a = -1;
　　Move[NW].b = -1;
}
class Items
{
public:
　　int x,y,dir;
　　Items(int i,int j,int d)
　　{
　　　　x = i;
　　　　y = j;
　　　　dir = d;
　　}
};

template<class T>
void funtion2(stack<T> &s)
{
　　stack<Items> stack;
　　while(!s.empty())
　　{
　　　　stack.push(s.top());
　　　　s.pop();
　　}
　　while (!stack.empty())
　　{
　　　　Items item = stack.top();
　　　　cout<<item.x<<','<<item.y<<','<<item.dir;
　　　　stack.pop();
　　　　cout<<endl;
　　}
}
void Path(int m,int p)
{
//Start at (1,1)
　　mark[1][1] = 1;
　　stack<Items> stack ;
　　Items temp(1,1,N);
　　stack.push(temp);
　　while(! stack.empty())
　　{//stack not empty
　　　　temp = stack.top();
　　　　stack.pop();
　　　　int i = temp.x;
　　　　int j = temp.y;
　　　　int d = temp.dir;
　　while(d<8)
　　{
　　　　int g = i+Move[d].a;
　　　　int h = i+Move[d].b;
　　　　if(g == m && h ==p )
　　　　{
　　　　　　funtion2(stack);
　　　　　　cout<<i<<" "<<j<<endl;
　　　　　　cout<<m<<" "<<p<<endl;
　　　　　　return;
　　　　}
　　　　if((!maze[g][h]) && (!mark[g][h]))
　　　　{
　　　　　　mark[g][h] = 1;
　　　　　　temp.x = i;
　　　　　　temp.y = j;
　　　　　　temp.dir = d+1;
　　　　　　stack.push(temp);
　　　　　　i = g;j = h;d = N;
　　　　}
　　　　else
　　　　　　d++;　

　　}　
　　}
　　cout<<"No path in maze."<<endl;
}

int main()
{
　　funtion1();
　　Path(m,p);
}

 

 

 

 

作者：蒋继发

2013/5/22