算法系列:贪心算法
贪婪算法的基本思想:通过一系列步骤来构造问题的解,每一步都是对已构造的部分解的一个扩展,直到获得问题的完整解。
贪婪算法中,每一步“贪婪地” 选择最好的部分解,但不顾及这样选择对整体的影响(局部最优),因此得到的全局解不一定最好的解,但对许多问题它能产生整体最优解。
具体算法描述:
1: void Knapsack(int n,float M, float v[], float w[], float x[])
2: {
3: Sort(n, v, w);
4: int i;
5: for(i = 1; i < n; i++)
6: x[i] = 0;
7: float c = M;
8: for(i = 1; i < n; i++)
9: {
10: if(w[i] > c)
11: break;
12: x[i] = 1;
13: c -= w[i];
14: }
15: if(i <=n)
16: x[i] = c/w[i];
17:
贪婪算法每一步需要满足3个条件:
1.可行性:即必须满足问题的约束。
2.局部最优:它是当前步骤中所有可行选择中最佳的局部选择。
3.不可取消:选择一旦做出,在后面的步骤中就无法改变。
贪心算法的基本要素:
1.贪心选择性质:指所求问题的整体最优解可以通过一系列局部最优的选择,即贪心选择来达到。
2.最优子结构性质:指一个问题的最优解包含其子问题的最优解。
贪心算法与动态规划算法的异同:
相同点:都具有最优子结构性质。
不同点:动态规划算法通常以自底向上的方式解各子问题;而贪心算法则通常以自顶向下的方式进行;
下面研究2个经典的组合优化例题,并以此说明贪心算法与动态规划算法的主要差别。
0-1背包问题:
给定n种物品和一个背包。物品i的重量是Wi,其价值为Vi,背包的容量为C。应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
背包问题:
与0-1背包问题类似,所不同的是在选择物品i装入背包时,可以选择物品i的一部分,而不一定要全部装入背包,1≤i≤n。
这2类问题都具有最优子结构性质,极为相似;但背包问题可以用贪心算法求解;而0-1背包问题却不能用贪心算法求解。
对于0-1背包问题:
例:n=3 , w={10,20,30} ,v={60,100,120} ,c=30
什么是最好的部分解? ——不求单位价值。
按贪心法:选择价值最大的放入 : 全部放入第3个物品,价值120。
但这并不是最好的, 若1,2 物品的放入,总价值160。
对于背包问题:
例:n=3 w={10,20,30} v={60,100,120} c=50
单位价值:v/w={6,5,4}
因此,第一次挑一号物品全部装入, r=40,pv=60
第二次挑2号,全部装入r=20,pv=160
第三次挑3号,部分装入r=0,pv=160+80=240
相信大家也已经看出问题的所在了。事实上,在考虑0-1背包问题时,应比较选择该物品和不选择该物品所导致的最终方案,然后再作出最好选择。所以对于0-1背包问题,适合采用动态规划来求解。
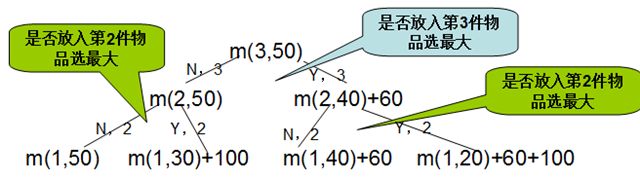
动态规划解0-1背包问题:
例:n=3 ,w={30,20,10} ,v={120, 100,60} ,c=50
m(i,j)是背包容量为j,可选择物品为1, 2,…,i时的最优值
Max=220,放入第一种,第二种