并查集

 并查集（Disjoint set或者Union-find set）是一种简单的用途广泛的算法和数据结构。并查集是若干个不相交集合，能够实现较快的合并和判断元素所在集合的操作，应用很多，如其求无向图的连通分量个数等。

并查集可以方便地进行以下三种操作：

1、Make_Set(x) 把每一个元素初始化为一个集合

初始化后每一个元素的父亲节点是它本身，每一个元素的祖先节点也是它本身（也可以根据情况而变）。

2、Find_Set(x) 查找一个元素所在的集合

查找一个元素所在的集合，其精髓是找到这个元素所在集合的祖先。这个才是并查集判断和合并的最终依据。

判断两个元素是否属于同一集合，只要看他们所在集合的祖先是否相同即可。

合并两个集合，也是使一个集合的祖先成为另一个集合的祖先，具体见示意图。

3、Union(x,y) 合并x,y 所在的两个集合

合并两个不相交集合操作很简单：

利用Find_Set找到其中两个集合的祖先，将一个集合的祖先指向另一个集合的祖先。如图

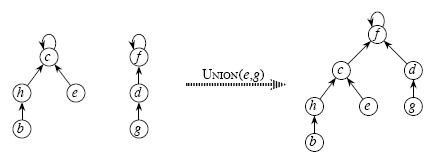
并查集的优化：

1、Find_Set(x)时 路径压缩

寻找祖先时我们一般采用递归查找，但是当元素很多亦或是整棵树变为一条链时，每次Find_Set(x)都是O(n)的复杂度，有没有办法减小这个复杂度呢？

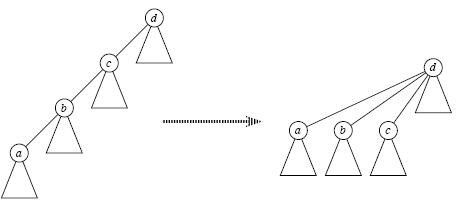
答案是肯定的，这就是路径压缩，即当我们经过"递推"找到祖先节点后，"回溯"的时候顺便将它的子孙节点都直接指向祖先，这样以后再次Find_Set(x)时复杂度就变成O(1)了，如下图所示；可见，路径压缩方便了以后的查找。

这两种技术可以互补，可以应用到另一个上，每个操作的平均时间仅为$O(\alpha(n))$，$\alpha(n)$是n = f(x) = A(x,x)的反函数，并且A是急速增加的阿克曼函数。因为$\alpha(n)$是其的反函数，$\alpha(n)$对于可观的巨大n还是小于5。因此，平均运行时间是一个极小的常数。

2、Union(x,y)时 按秩合并

即合并的时候将元素少的集合合并到元素多的集合中，这样合并之后树的高度会相对较小。

有了背景知识，我们来看如何利用它来解决：

给一个整数数组， 找到其中包含最多连续数的子集，比如给：15, 7, 12, 6, 14, 13, 9, 11，则返回: 5:[11, 12, 13, 14, 15] 。最简单的方法是sort然后scan一遍，但是要o(nlgn)，有什么O(n)的方法吗？

首先，Make_Set(x)将每个元素变成一个并查集，然后扫描，Union(x-1, x)，Union(x, x+1)。

接下来的问题是怎么快速找到x-1,x+1的位置？那么需要引入查找为常数复杂度的哈希表。

 1 #include <iostream>

 2 #include<hash_map>

 3 using namespace std;

 4 

 5 const int MAX = 100;

 6 int Father[MAX];

 7 int Rank[MAX];

 8 

 9 void MakeSet(int x){

10     Father[x] = x;

11     Rank[x] = 1;

12 }

13 

14 int FindFather(int x){

15     if(x != Father[x])

16         Father[x] = FindFather(Father[x]);

17     return Father[x];

18 }

19 

20 void Union(int x, int y){

21     int a = FindFather(x);

22     int b = FindFather(y);

23     if(a == b)

24         return;

25     else{

26         int ar = Rank[a];

27         int br = Rank[b];

28         if(ar <= br){

29             Father[a] = b;

30             Rank[b] += Rank[a];

31         }else{

32             Father[b] = a;

33             Rank[a] += Rank[b];

34         }

35     }

36 }

37 

38 int main()

39 {

40     const int length = 15;

41     int arr[length] = {15, 7, 12, 6, 14, 13, 10, 11, 4, 5, 8, 3, 2, 16, 17};

42     hash_map<int,int> ihmap;

43     for(int i = 0; i < length; ++i)

44     {

45         MakeSet(i);

46         ihmap[arr[i]]=i;

47     }

48 

49     for(int i = 0; i < length; ++i)

50     {

51         hash_map<int,int>::iterator tmp;

52         tmp = ihmap.find(arr[i]-1);

53         if(tmp != ihmap.end())

54         {

55             Union(i,tmp->second);            

56         }

57         tmp = ihmap.find(arr[i]+1);

58         if(tmp != ihmap.end())

59         {

60             Union(i,tmp->second);            

61         }

62     }

63     int max = Rank[0];

64     int father = 0;

65     for(int i = 1; i< length; ++i)

66         if(Rank[i]>max){

67             max = Rank[i];

68             father = i;

69         }

70     cout<<max<<endl;

71 

72     for(int i = 0; i< length; ++i)

73         if(Father[i] == father)

74             cout<<arr[i]<<' ';

75     cout<<endl;

76 

77     return 0;

78 }

 

转自：http://blog.csdn.net/doc_sgl/article/details/11667301