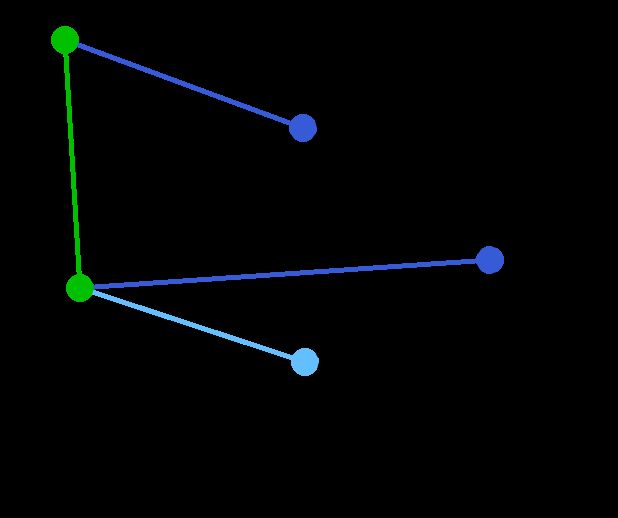
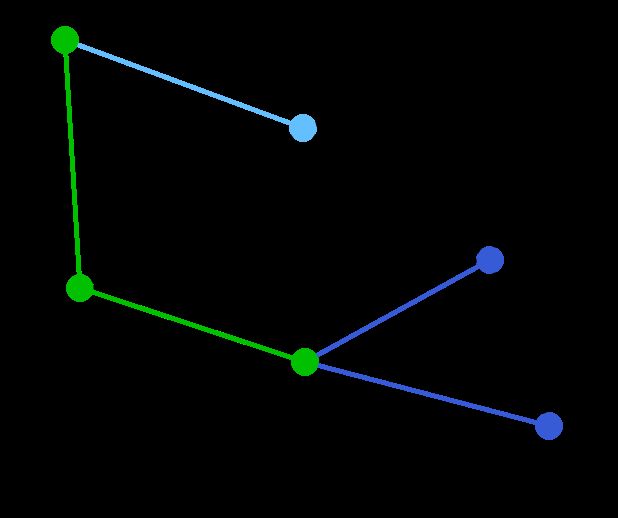
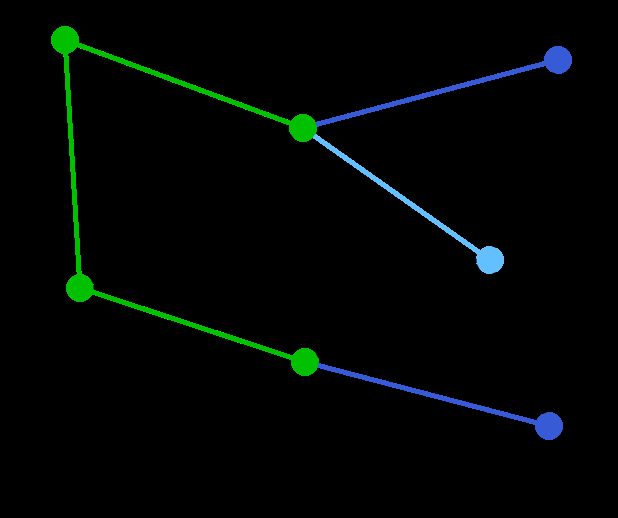
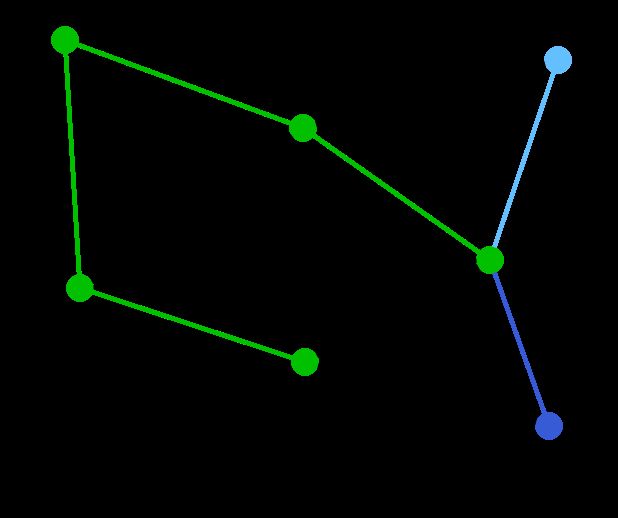
图的最小生成树与最短路径
带权图分为有向和无向，
无向图的最短路径又叫做最小生成树，有prime算法和kruskal算法；
生成树的概念：联通图G的一个子图如果是一棵包含G的所有顶点的树，则该子图称为G的生成树 生成树是联通图的极小连通子图。所谓极小是指：若在树中任意增加一条边，则 将出现一个回路；若去掉一条边，将会使之编程非连通图。生成树各边的权 值总和称为生成素的权。权最小的生成树称为最小生成树，常用的算法有prime算法和kruskal算法。
最短路径问题旨在寻找图中两节点之间的最短路径，常用的算法有：floyd算法和dijkstra算法。
prime算法
普里姆算法（Prim算法），图论中的一种算法，可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中，不但包括了连通图里的所有顶点（英语：Vertex (graph theory)），且其所有边的权值之和亦为最小。
算法简单描述
1).输入：一个加权连通图，其中顶点集合为V，边集合为E；
2).初始化：Vnew = {x}，其中x为集合V中的任一节点（起始点），Enew = {},为空；
3).重复下列操作，直到Vnew = V：
a.在集合E中选取权值最小的边<u, v>，其中u为集合Vnew中的元素，而v不在Vnew集合当中，并且v∈V（如果存在有多条满足前述条件即具有相同权值的边，则可任意选取其中之一）；
b.将v加入集合Vnew中，将<u, v>边加入集合Enew中；
4).输出：使用集合Vnew和Enew来描述所得到的最小生成树。
| 图例 | 说明 | 不可选 | 可选 | 已选（Vnew） |
|---|---|---|---|---|
|
|
此为原始的加权连通图。每条边一侧的数字代表其权值。 | - | - | - |
|
顶点D被任意选为起始点。顶点A、B、E和F通过单条边与D相连。A是距离D最近的顶点，因此将A及对应边AD以高亮表示。 | C, G | A, B, E, F | D |
|
|
下一个顶点为距离D或A最近的顶点。B距D为9，距A为7，E为15，F为6。因此，F距D或A最近，因此将顶点F与相应边DF以高亮表示。 | C, G | B, E, F | A, D |
 |
算法继续重复上面的步骤。距离A为7的顶点B被高亮表示。 | C | B, E, G | A, D, F |
|
|
在当前情况下，可以在C、E与G间进行选择。C距B为8，E距B为7，G距F为11。E最近，因此将顶点E与相应边BE高亮表示。 | 无 | C, E, G | A, D, F, B |
|
|
这里，可供选择的顶点只有C和G。C距E为5，G距E为9，故选取C，并与边EC一同高亮表示。 | 无 | C, G | A, D, F, B, E |
|
顶点G是唯一剩下的顶点，它距F为11，距E为9，E最近，故高亮表示G及相应边EG。 | 无 | G | A, D, F, B, E, C |
|
现在，所有顶点均已被选取，图中绿色部分即为连通图的最小生成树。在此例中，最小生成树的权值之和为39。 | 无 | 无 | A, D, F, B, E, C, G |
kruskal算法
构造一个只含n个顶点，而边集为空的子图，若将该子图中各个顶点看成是各棵树的根节点，则它是一个含有n棵树的森林 。之后，从网的边集中选取一条权值最小的边，若该边的两个顶点分属不同的树 ，则将其加入子图，也就是这两个顶点分别所在的 两棵树合成一棵树；反之，若该边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之。依次类推，直至森林只有一棵树。kruskal算法能够在并查集的基础很快的实现。
floyd算法
1)算法思想原理：
Floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话，首先我们的目标是寻找从点i到点j的最短路径。从动态规划的角度看问题，我们需要为这个目标重新做一个诠释（这个诠释正是动态规划最富创造力的精华所在）
从任意节点i到任意节点j的最短路径不外乎2种可能，1是直接从i到j，2是从i经过若干个节点k到j。所以，我们假设Dis(i,j)为节点u到节点v的最短路径的距离，对于每一个节点k，我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立，如果成立，证明从i到k再到j的路径比i直接到j的路径短，我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j)，这样一来，当我们遍历完所有节点k，Dis(i,j)中记录的便是i到j的最短路径的距离。
2).算法描述：
a.从任意一条单边路径开始。所有两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大。
b.对于每一对顶点 u 和 v，看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。
void floyd()
{
for(int k = 0; k < n; k ++){ //作为循环中间点的k必须放在最外一层循环
for(int i = 0; i < n; i ++){
for(int j = 0; j < n; j ++){
if(dist[i][j] > dist[i][k] + dist[k][j]){
dist[i][j] = dist[i][k] + dist[k][j]; //dist[i][j]得出的是i到j的最短路径
}
}
}
}
}
Dijkstra算法
1)算法思想：设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 , 就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了），第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的顶点的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
2)算法步骤：
a.初始时，S只包含源点，即S＝{v}，v的距离为0。U包含除v外的其他顶点，即:U={其余顶点}，若v与U中顶点u有边，则<u,v>正常有权值，若u不是v的出边邻接点，则<u,v>权值为∞。
b.从U中选取一个距离v最小的顶点k，把k，加入S中（该选定的距离就是v到k的最短路径长度）。
c.以k为新考虑的中间点，修改U中各顶点的距离；若从源点v到顶点u的距离（经过顶点k）比原来距离（不经过顶点k）短，则修改顶点u的距离值，修改后的距离值的顶点k的距离加上边上的权。
d.重复步骤b和c直到所有顶点都包含在S中。
用Dijkstra算法找出以A为起点的单源最短路径步骤如下
const int MAXINT = 32767;
const int MAXNUM = 10;
int dist[MAXNUM];
int prev[MAXNUM];
int A[MAXUNM][MAXNUM];
void Dijkstra(int v0)
{
bool S[MAXNUM]; // 判断是否已存入该点到S集合中
int n=MAXNUM;
for(int i=1; i<=n; ++i)
{
dist[i] = A[v0][i];
S[i] = false; // 初始都未用过该点
if(dist[i] == MAXINT)
prev[i] = -1;
else
prev[i] = v0;
}
dist[v0] = 0;
S[v0] = true;
for(int i=2; i<=n; i++)
{
int mindist = MAXINT;
int u = v0; // 找出当前未使用的点j的dist[j]最小值
for(int j=1; j<=n; ++j)
if((!S[j]) && dist[j]<mindist)
{
u = j; // u保存当前邻接点中距离最小的点的号码
mindist = dist[j];
}
S[u] = true;
for(int j=1; j<=n; j++)
if((!S[j]) && A[u][j]<MAXINT)
{
if(dist[u] + A[u][j] < dist[j]) //在通过新加入的u点路径找到离v0点更短的路径
{
dist[j] = dist[u] + A[u][j]; //更新dist
prev[j] = u; //记录前驱顶点
}
}
}
}
reference：http://www.cnblogs.com/biyeymyhjob/archive/2012/07/30/2615542.html