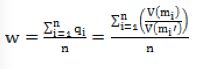围棋博弈程序的实现与思考（1）——局面评估

        毕业也有两个月了，写这篇文章算是纪念我的毕设——围棋博弈程序的设计与实现。选了这个找抽的课题作为毕设，一度不知该如何实现，还好万能的微博让我得知了现代计算机围棋的核心算法——UCT算法。而蒙特卡罗局面评估算法是UCT算法的基础。本文作为本系列第一篇文章，先介绍蒙特卡罗局面评估算法。

        计算机围棋博弈问题的一大难点在于难以设计简单有效的局面评估算法。传统的围棋程序主要采用影响函数等专家知识进行局面评估，由于围棋的专家知识难以抽象出来（想想厚味，薄味，气合等词……），往往评估得不准。so怎样才能精确评估呢？穷举！没错，如果黑白双方的接下来每手棋都“正确”，最后黑棋赢了，那么当时的局面一定是黑棋优势。

        量子计算机还没干出来，还是想点可行的方法吧——再假设，如果黑白双方棋力不高却相当，来续下这个局面，最后是黑棋赢了，当时的局面是谁优势呢？你大概会说，黑棋优势的可能性更大一些。进一步，同样的局面续下了1000次，有800次是黑棋赢了，你是不是基本相信黑棋优势呢？

        那么，如果黑棋和白棋都不会围棋，只会随机落子呢？他们针对这一局面续下了1000次，竟然有800次是黑棋赢了……

        这就是蒙特卡罗局面评估算法，so easy~

＊＊＊＊＊＊＊＊＊＊＊＊分割线＊＊＊＊＊＊＊＊＊＊＊＊＊＊

        论文中有些不自量力，试图从数学上探讨蒙特卡罗局面评估算法的合理性（后来才知道早就有人证明了），以下贴论文……

3.3.4 一种围棋“棋步价值”的数学定义与精确量化的方法

    Monte Carlo方法的理论依据是概率统计学中的“大数定理”。在本节中，我将试图从数学的角度对MonteCarlo方法应用于围棋局面评估的合理性作一些探讨。

    总的想法是：围棋中每一手棋的价值都是可以用数学的方法精确量化的，本文提出一种对于“棋步价值”的数学定义（以及一系列围棋领域中相关概念的数学定义），同时也是精确量化“棋步价值”的方法。

    首先，对于围棋这样的完备信息的零和博弈游戏而言，对于任意一个给定的局面，对于落子方而言客观上一定存在“最佳棋步”（使己方在终局时领地最多的棋步），并且理论上可以通过穷举法来找到“最佳棋步”，以下给出穷举法递归实现的伪代码：

 

表3-7 伪代码2

Move bestMove(GoBoard board) {     for (move in board.next_move_set) {         next_board = board.move(move);         value = bestMove(next_board);         用best_move记录本循环value的最大值;     }     return best_move; }

 

    设围棋局面的集合为S，对弈双方为 ，当前局面的可下点集合为 ，那么对于局面 ,玩家 ，若有棋步 , 则存在棋步m的价值函数 ， 的计算步骤如下：

1)     对于局面a，记棋步m后的局面为b，之后双方都应以“最佳棋步”，终局时p收益计为C。

2)     对于局面a，p方pass（也就是改变落子方），之后双方都应以“最佳棋步”，终局时p得收益D。

3)     V(m) = C - D。

    于是“最佳棋步”又可以定义为，令 取最大值的m，记为m'。易得，“棋步价值” 也是一个递归定义。容易想到， 还可用来表征局面a的“激烈程度”。

    根据以上的定义又可以引入“棋步质量”的概念，“棋步质量” 。当 时，即“最佳棋步”，当q= 0时，即通常所说的“废棋（没有价值的棋）”。当棋局已结束时（即m'=0），“棋步质量”q无定义。

    进一步地，可以对围棋中的常用名词“棋力”（形容一个人围棋水平高低）给出数学定义：设某人一段时间来以来（或某一局棋中）产生的棋步集合为 ，则此人的“棋力”计算式如下：

                                                      

    “棋力”w也就是“棋步质量”的平均值。需要指出的是，“棋力”是一个对局者本身固有的属性，上式仅仅是它的求值方法，这个情况类似于电学公式 。

    基于以上的数学定义，我认为要从数学上证明Monte Carlo方法应用围棋局面评估的合理性，需要证明以下2个猜想：

1)      对于给定局面a，双方都应以最佳棋步，得终局收益A。同样对于局面a，由两个“棋力”相等的对局者续下，终局收益的数学期望为B。则A约等于B。

2)      一个只会产生随机棋步的下棋者r，通过大量的对局可以得出r的“棋力”R，R是一个未知常数。

    本文未能对以上2个猜想给出数学证明，但我个人相信这2个猜想都是正确的。

＊＊＊＊＊＊分割线＊＊＊＊＊＊＊＊

        最后没能证明，最后一句话有点无赖………