最短路径顶点算法:最短路径之迪杰斯特拉(Dijkstra)算法Strut2教程-java教程
发一下牢骚和主题无关:
对于网图说来,最短路径,是指两顶点之间经过的边上权值之和少最的路径,并且我们称路径上的第一个顶点为源点,最后一个顶点为终点。最短路径的算法主要有迪杰斯特拉(Dijkstra)算法和弗洛伊德(Floyd)算法。本文先来讲第一种,从某个源点到其余各顶点的最短路径题问。
这是一个按路径长度递增的顺序发生最短路径的算法,它的大致思绪是这样的。
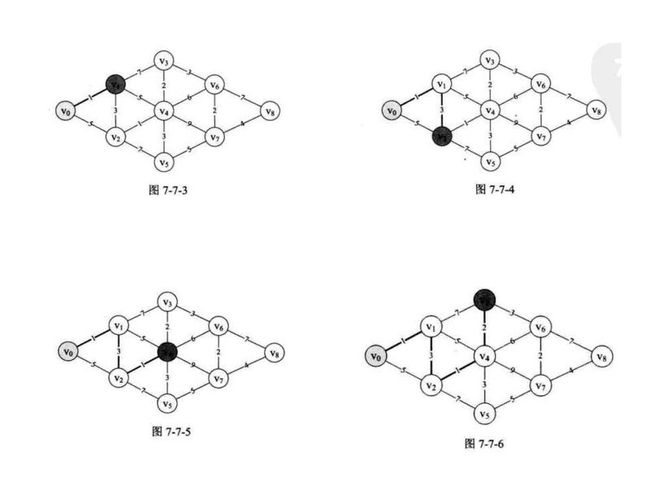
比如说要求图7-7-3中顶点v0到v1的最短路径,明显就是1。由于顶点v1还与v2,v3,v4连线,所以此时我们同时求得了v0->v1->v2 = 1+3 = 4, v0->v1->v3 = 1 +7 = 8, v0->v1->v4 = 1+5 = 6。
当初我们可以道知v0到v2的最短离距为4而不是v0->v2 直接连线的5,如图7-7-4所示。由于顶点v2还与v4,v5连线,所以同时我们求得了v0->v2->v4其实就是v0->v1->v2->v4 = 4+1=5,v0->v2->v5 = 4+7 = 11,这里v0->v2我们用的是刚才计算出来的小较的4。此时我们也发明v0->v1->v2->v4 = 5要比v0->v1->v4 = 6还要小,所以v0到v4的最短离距现在是5,如图7-7-5所示。
当我们要求v0到v3的最短路径时,通向v3的三条边,除了v6没有研究过外,v0->v1->v3 = 8, 而v0->v4->v3 = 5 +2 = 7,因此v0到v3的最短路径为7,如图7-7-6所示。
如上所示,这个算法是不并一会儿就求出来v0到v8的最短路径,而是一步步求出它们之间顶点的最短离距,过程当中都是基于经已求出的最短路径的基础上,求得更远顶点的最短路径,终最到得想要的结果。
程序代码如下:(改编自《话大数据结构》)
|
1
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 |
#include<iostream>
using namespace std; #define MAXEDGE 20 #define MAXVEX 20 #define INFINITY 65535 typedef struct { int vexs[MAXVEX]; int arc[MAXVEX][MAXVEX]; int numVertexes, numEdges; } MGraph; typedef int PathArc[MAXVEX]; typedef int ShortPathTable[MAXVEX]; /* 构建图 */ void CreateMGraph(MGraph *G) { int i, j; /* printf("请输入边数和顶点数:"); */ G->numEdges = 16; G->numVertexes = 9; for (i = 0; i < G->numVertexes; i++) /* 初始化图 */ { G->vexs[i] = i; } for (i = 0; i < G->numVertexes; i++) /* 初始化图 */ { for ( j = 0; j < G->numVertexes; j++) { if (i == j) G->arc[i][j] = 0; else G->arc[i][j] = G->arc[j][i] = INFINITY; } } G->arc[ 0][ 1] = 1; G->arc[ 0][ 2] = 5; G->arc[ 1][ 2] = 3; G->arc[ 1][ 3] = 7; G->arc[ 1][ 4] = 5; G->arc[ 2][ 4] = 1; G->arc[ 2][ 5] = 7; G->arc[ 3][ 4] = 2; G->arc[ 3][ 6] = 3; G->arc[ 4][ 5] = 3; G->arc[ 4][ 6] = 6; G->arc[ 4][ 7] = 9; G->arc[ 5][ 7] = 5; G->arc[ 6][ 7] = 2; G->arc[ 6][ 8] = 7; G->arc[ 7][ 8] = 4; for(i = 0; i < G->numVertexes; i++) { for(j = i; j < G->numVertexes; j++) { G->arc[j][i] = G->arc[i][j]; } } } /* Dijkstra算法,求有向网G的pos顶点到其余顶点v的最短路径P[v]及带权长度D[v] */ /* P[v]的值为前驱顶点下标,D[v]表示pos到v的最短路径长度和 */ /* pos 取值 0~MG.numVertexs-1 */ void ShortestPath_Dijkstra(MGraph MG, int pos, PathArc P, ShortPathTable D) { int v, w, k, min; int final[MAXVEX]; /* final[w]=1表示求得顶点pos至w的最短路径 */ for (v = 0; v < MG.numVertexes; v++) { final[v] = 0; /* 全部顶点初始化为未知最短路径状态 */ D[v] = MG.arc[pos][v]; /* 将与pos点有连线的顶点加上权值 */ P[v] = 0; /* 初始化路径数组P为0 */ } D[pos] = 0; /*说明源点pos没有到自身的路径 */ P[pos] = - 1; /* -1表示自身无前驱顶点*/ final[pos] = 1; /* pos至pos不需要求路径 */ /* 开始主循环,每次求得pos到某个v顶点的最短路径 */ for (v = 1; v < MG.numVertexes; v++) { min = INFINITY; /* 当前所知离pos顶点的最近离距 */ for (w = 0; w < MG.numVertexes; w++) /* 寻找离pos最近的顶点 */ { if (!final[w] && D[w] < min) { k = w; min = D[w]; /* w顶点离pos顶点更近 */ } } final[k] = 1; /* 将现在找到的最近的顶点置为1 */ for (w = 0; w < MG.numVertexes; w++) /* 修正当前最短路径及离距 */ { if (!final[w] && (min + MG.arc[k][w] < D[w])) { /* 说明找到了更短的路径,修改D[w]和P[w] */ D[w] = min + MG.arc[k][w]; /* 修改当前路径长度 */ P[w] = k; } } } /* 结束循环,若P[w] = 0;说明顶点w的前驱为pos */ } int main( void) { MGraph MG; PathArc P; ShortPathTable D; int i, j, pos = 2; CreateMGraph(&MG); ShortestPath_Dijkstra(MG, pos, P, D); cout << "逆序最短路径如下:" << endl; for (i = 8; i >= 0; i--) { j = i; while (P[j] != - 1 && P[j] != 0) { cout << "v" << j << "<-" << "v" << P[j] << " "; j = P[j]; } cout << "v" << j << "<-" << "v" << pos << " "; cout << endl; } cout << endl; return 0; } |
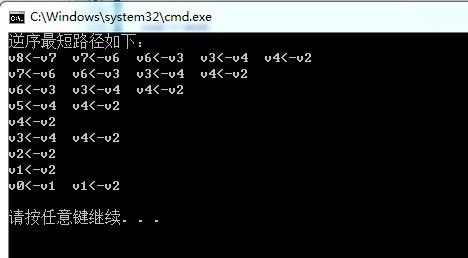
输出为:
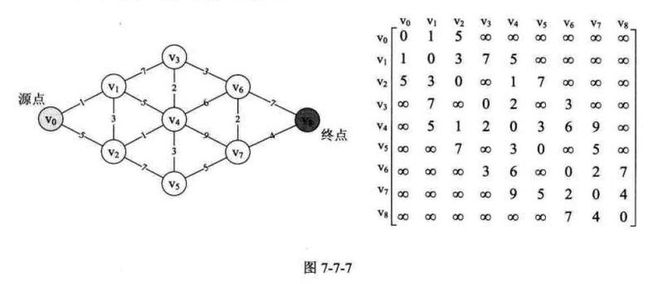
其中CreateMGraph函数创建出来的邻接矩阵如图7-7-7所示。
相信经过上面的分析,大家可以自己进行循环跑程序分析了,循环结束后final = { 1, 1, 1, 1, 1, 1, 1, 1, 1 }表示所有顶点均完成了最短路径的查找工作。此时D = { 4, 3, 0, 3, 1, 4, 6, 8, 12 }, 注意我们在前面说过Dijkstra算法可以求某个源点到其他顶点的最短路径,当初我们上面程序中给出的pos = 2, 即源点为v2, 所以D[2] = 0 表示没有到自身的路径。D数组表示v2到各个顶点的最短路径长度,比如D[8] =1+2 + 3 + 2 + 4 = 12。此时P = { 1, 0, -1, 4, 0, 4, 3, 6, 7 }, 可以这样来理解,P[2] = -1 表示v2没有前驱顶点,P[1] = P[4] = 0 表示v1和v4的前驱顶点为源点v2。再比如P[8] = 7,表示v8的前驱是v7;再由P[7] = 6,表示v7的前驱是v6; P[6] = 3 表示v6的前驱是v3, 这样就可以到得v2 到 v8的最短路径为v2->v4->v3->v6->v7->v8,从上面的程序输出也可以验证我们的推测。
其实终最返回的数组D和数组P,是可以到得v2到任意一个顶点的最短路径和路径长度的,也就是说我们通过Dijkstra算法解决了从某个源点到其余各顶点的最短路径题问。从循环嵌套可以到得此算法的时间复杂度为O(n^2),如果我们要到得任一顶点到其余顶点的最短路径呢?最简单的办法就是对每个顶点都当作源点进行一次Dijkstra算法,等于在原有算法的基础上,再来一次循环,此时整个算法的时间复杂度就为O(n^3)。
文章结束给大家分享下程序员的一些笑话语录: 雅虎最擅长的不是开通新业务,是关闭旧业务。