简介
关于Hanoi塔问题的分析,在网上的文章都写烂了。之所以打算写这篇文章,更多的是针对这个问题相关的各种数学思路和代码实现过程做一个总结。它虽然是一个看似简单的问题,后面引申出来的问题推导方法和思路还是比较丰富的。
问题描述
这个问题起源于一个类似传说故事,在Hanoi这个地方有一个寺庙,这里有3根柱子和64个大小不同的金碟子。每个碟子有一个孔可以穿过。所有的碟子都放在第一个柱子上,而且按照从上到下碟子的大小依次增大的顺序摆设。如下图:
现在,假定寺庙里的僧侣要移动这些碟子,将它们从最左边移动到最右边的柱子上。不过移动的规则如下:
1. 每次只能从一个柱子的最上面移动一个碟子到另外一个柱子上。
2. 不能将大碟子放到小碟子的上面。
按照前面这个规则,我们该怎么去移动这些碟子呢?假定单位时间内可以移动一片碟子,那么最终移动这些碟子到目的柱子需要多长的时间呢?
问题分析
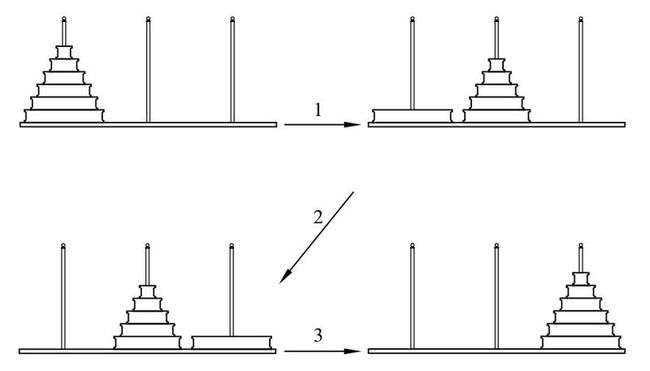
在分析这个问题的时候,我们可以先从一些简单的场景来看怎么来移动碟子保证可以达到目的。假定我们有3个碟子,那么移动它们的过程如下图:
我们假定柱子从左到右分别为a, b, c。从前面移动碟子的步骤可以看到,我们要将a上面的两个碟子先移动到中间的b柱子作为过渡,然后再将最下面的柱子移动到目的c柱子,然后再将上面的两个碟子移过来。在将最下面的碟子移动到c之前,首先的步骤1, 2, 3是将上面的碟子移动到柱子b。而将最下面碟子移动后,上面的两个碟子又要移动一遍,不过是从b移动到c,只是借助的柱子不一样。
所以,从上面的过程,我们可以看到一个可以递归解决问题的思路,如下图:
如图所示,首先我们针对有n个碟子的柱子a,将n-1个碟子移动到柱子b。假定这个问题为S(n)表示移动的步数,则上面的问题是S(n)的一个子问题S(n-1)。这一步对应步骤1。然后将最下面的碟子移动到柱子c,最后再将n-1个碟子移动到c。后面这一步也相当于S(n)的子问题S(n-1)。对应步骤3.它和前面第一步移动n-1个碟子唯一不同的地方在于第一步是借助c将n-1个碟子从a移动到b,而最后这一步是借助a将n-1个碟子从b移动到c。除了借助的柱子和目的柱子不一样,其他的都是一样的。
这样我们就可以很容易得到一个这样的推导关系:
S(n) = 2S(n - 1) +1
再考虑一种初始的情况,假定只有一个碟子需要移动,我们直接将碟子从a移动到c,那么需要的步骤是1步。因此可以说S(1) = 1。
进一步推导
有了前面的归纳关系,我们可以很容易得到如下的一组推导结果:
S(1) = 1
S(2) = 2 x S(1) + 1 = 2 + 1 = 3
S(3) = 2 x S(2) + 1 = 2 x 3 + 1 = 7
S(4) = 2 x S(3) +1 = 2 x 7 + 1 = 15
从这些得出来的结果里,似乎还看不到多少有规律的地方。不过我们可以采取一种根据递推原则代换的方式来尝试发现规律。前面的推导关系里有S(n) = 2 x S(n - 1) +1,那么我们将有如下的推导:
这里,我们发现什么规律没?原来,这里似乎符合如下的一个等式:
当我们最终一路递推到T1的时候,它将满足如下的形式:
这似乎是我们所求得的结果了。当然,这种推导也有可能会出错。最好的情况是我们还需要验证一下它。验证的方法可以考虑用数学归纳法。因为过程比较简单,这里就不再赘述了。最终可以验证出来结果是满足以上等式的。从前面的推导我们可以看出,最终要实现将64个碟子移动到目的柱子,需要的时间是2的64次方这个量级的。在一定程度上,用计算机的内置数据类型都没法表示这个数值。
代码实现
前面的分析可以发现,从计算机实现来说,这个问题是指数函数级别的,意味着它的增长速度非常快,在一定程度上计算机都无法解决。在一个比较小的数值范围内,我们还是可以做一个参考实现的。有了前面的讨论,我们的完整代码实现如下:
public class Hanoi {
public static void move(char a, char b, char c, int n) {
if(n == 0)
return;
move(a, c, b, n-1);
System.out.printf("Move disk %d from %s to %s\n", n, a, c);
move(b, c, a, n-1);
}
public static void main(String[] args) {
move('a', 'b', 'c', 3);
}
}
这部分代码里,我们递归的退出条件是当最终碟子移走,即n == 0。运行这一段程序的结果如下:
Move disk 1 from a to c Move disk 2 from a to b Move disk 1 from c to a Move disk 3 from a to c Move disk 1 from b to c Move disk 2 from b to a Move disk 1 from c to b
和前面图示的过程是完全一致的。当然,在提供的数值比较大的时候,我们这种递归的方式就溢出了。
总结
Hanoi塔问题是一个经典的递归问题,它本身的数学复杂度达到了指数函数级别。所以使得运算时间的增长非常快。通过一种递归的思路,首先我们可以总结出一个问题的递归描述方式。然后我们再通过不断的代入和分析,去发现形成等式的规律。这是一种发现递归问题等式描述的方法。为了保证方法最终的正确性,我们还需要经常使用数学归纳法来证明这个等式的正确性。
参考材料
mathematics for computer science