动态规划---求图中两点距离的Floyd算法
---Floyd算法用于解决有权图中顶点对之间的最短路径问题。
---A(k)表示一个矩阵,它的第ij个元素值表示从i到j的最短路径,而且允许的中间顶点只能是(1,2,3,……k)。
---A(0)表示此有权图的邻接矩阵。
---矩阵A(n)表示表示从i到j的最短路径,并且中间顶点可以是任意顶点。
---问题所求解即为A(n)。
---初始条件为A(0),然后根据递归条件依次计算A(1),A(2)……A(n)。
---递推关系推导:当我们由A(k-1)计算A(k)的时候,会多出一个可选择的顶点k,这时候就存在是否选择该顶点的问题,如果选择该顶点后的最短距离大于不选择该顶点的最短距离,那么最短路径就不经过该顶点,此时有 A(k)ij = A(k-1)ij,如果一旦选用该顶点,那么就说明选择该顶点后的最短距离小于不选择该顶点的最短距离,那么此时有 A(k)ij = A(k-1)ik + A(k-1)kj,所以根据是否选择该顶点k,可以得出Floyd的递推关系式: A(k)ij = min{ A(k-1)ij , A(k-1)ik + A(k-1)kj }
---当我们使用A(k-1)生成A(k)的时候,它并不是创建一个新的矩阵的过程,而是用A(k)计算出的新值替代A(k-1)的旧值的过程,这种计算成为替代操作。我们有 A(k)ij = min{ A(k-1)ij , A(k-1)ik + A(k-1)kj },在计算的时候,如果A(k-1)ik 和 A(k-1)kj 算出之后 ,那么它就有被替换的可能,变成 A(k)ik 和 A(k)kj ,那么当计算A(k)ij的时候,它使用的就不是A(k-1)ik 和 A(k-1)kj ,而是新的 A(k)ik 和 A(k)kj ,但是,这些值实际上均未发生变化。因为 A(k)ik = A(k-1)ik,A(k)kj =A(k-1)kj,因为在其中k并未充当中间节点,而是终点和起点,所以不用担心这个问题。
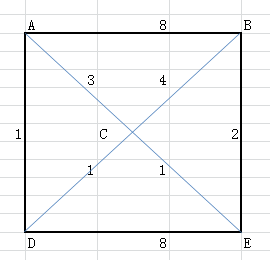
---eg:求各点之间最短距离
edtion1:
package demo;
public class Demo {
public static void Floyd( int[][] A0){
//第一层for循环,因为顶点我们要一个个往里加
for ( int k = 0; k < A0. length; k++) {
//遍历二维数组
for ( int i = 0; i < A0. length; i++) {
for ( int j = 0; j < A0. length; j++) {
if(A0[i][j]>A0[i][k]+A0[k][j]){
A0[i][j]=A0[i][k]+A0[k][j];
}
}
}
print(A0,k+1);
}
}
//打印输出新得到的A[i]
public static void print( int[][] A, int count){
/**
* 邻接矩阵(初始条件)
*/
System. out.println( "A["+count+ "]"+ "矩阵为:");
for ( int i = 0; i < A. length; i++) {
for ( int j = 0; j < A. length; j++) {
System. out.print(A[i][j]+ "\t");
}
System. out.println();
}
}
public static void main(String[] args) {
//大数来表示无穷大
int max = 1000;
int[][] A0 = {
{ 0, 8, 3, 1,max },
{ 8, 0, 4, max, 2 },
{ 3, 4, 0, 1, 1 },
{ 1, max, 1, 0, 8 },
{ max, 2, 1, 8, 0 }
};
Floyd(A0);
}
}
结果:
A[1]矩阵为:
0 8 3 1 1000
8 0 4 9 2
3 4 0 1 1
1 9 1 0 8
1000 2 1 8 0
A[2]矩阵为:
0 8 3 1 10
8 0 4 9 2
3 4 0 1 1
1 9 1 0 8
10 2 1 8 0
A[3]矩阵为:
0 7 3 1 4
7 0 4 5 2
3 4 0 1 1
1 5 1 0 2
4 2 1 2 0
A[4]矩阵为:
0 6 2 1 3
6 0 4 5 2
2 4 0 1 1
1 5 1 0 2
3 2 1 2 0
A[5]矩阵为:
0 5 2 1 3
5 0 3 4 2
2 3 0 1 1
1 4 1 0 2
3 2 1 2 0
----输出最短路径上紧跟顶点i的结点,用next[i][j]保存
editon2:
public class Demo2 {
public static void Floyd( int[][] A0, int[][] next){
//第一层for循环,因为顶点我们要一个个往里加
for ( int k = 0; k < A0. length; k++) {
//遍历二维数组
for ( int i = 0; i < A0. length; i++) {
for ( int j = 0; j < A0. length; j++) {
if(A0[i][j]>A0[i][k]+A0[k][j]){
A0[i][j]=A0[i][k]+A0[k][j];
next[i][j] = next[i][k];
}
}
}
System. out.println( "对应A矩阵为:" );
print(A0,k+1);
System. out.println( "对应next矩阵为:" );
print(next,k+1);
System. out.println( "~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~" );
}
}
//打印输出新得到的A[i]
public static void print( int[][] arr, int count){
/**
* 邻接矩阵(初始条件)
*/
System. out.println( "["+count+ "]"+ "矩阵为:");
for ( int i = 0; i < arr. length; i++) {
for ( int j = 0; j < arr. length; j++) {
System. out.print(arr[i][j]+ "\t");
}
System. out.println();
}
}
public static void main(String[] args) {
//大数来表示无穷大
int max = 1000;
int[][] A0 = {
{ 0, 8, 3, 1,max },
{ 8, 0, 4, max, 2 },
{ 3, 4, 0, 1, 1 },
{ 1, max, 1, 0, 8 },
{ max, 2, 1, 8, 0 }
};
int[][] next = new int[A0. length][A0. length];
/**
* 初始化next矩阵,用next矩阵存储i到j最短路径上紧跟i后的顶点
* 刚开始全部初始化为j
*/
for ( int i = 0; i < next. length; i++) {
for ( int j = 0; j < next. length; j++) {
next[i][j]=j+1;
}
}
Floyd(A0,next);
}
}
输出结果:
对应A矩阵为:
[1]矩阵为:
0 8 3 1 1000
8 0 4 9 2
3 4 0 1 1
1 9 1 0 8
1000 2 1 8 0
对应next矩阵为:
[1]矩阵为:
1 2 3 4 5
1 2 3 1 5
1 2 3 4 5
1 1 3 4 5
1 2 3 4 5
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
对应A矩阵为:
[2]矩阵为:
0 8 3 1 10
8 0 4 9 2
3 4 0 1 1
1 9 1 0 8
10 2 1 8 0
对应next矩阵为:
[2]矩阵为:
1 2 3 4 2
1 2 3 1 5
1 2 3 4 5
1 1 3 4 5
2 2 3 4 5
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
对应A矩阵为:
[3]矩阵为:
0 7 3 1 4
7 0 4 5 2
3 4 0 1 1
1 5 1 0 2
4 2 1 2 0
对应next矩阵为:
[3]矩阵为:
1 3 3 4 3
3 2 3 3 5
1 2 3 4 5
1 3 3 4 3
3 2 3 3 5
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
对应A矩阵为:
[4]矩阵为:
0 6 2 1 3
6 0 4 5 2
2 4 0 1 1
1 5 1 0 2
3 2 1 2 0
对应next矩阵为:
[4]矩阵为:
1 4 4 4 4
3 2 3 3 5
4 2 3 4 5
1 3 3 4 3
3 2 3 3 5
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
对应A矩阵为:
[5]矩阵为:
0 5 2 1 3
5 0 3 4 2
2 3 0 1 1
1 4 1 0 2
3 2 1 2 0
对应next矩阵为:
[5]矩阵为:
1 4 4 4 4
5 2 5 5 5
4 5 3 4 5
1 3 3 4 3
3 2 3 3 5
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
editon3:打印两个顶点之间的最短路径所经过的顶点
public class Demo3 {
public static void Floyd( int[][] A0, int[][] next) {
// 第一层for循环,因为顶点我们要一个个往里加
for ( int k = 0; k < A0. length; k++) {
// 遍历二维数组
for ( int i = 0; i < A0. length; i++) {
for ( int j = 0; j < A0. length; j++) {
if (A0[i][j] > A0[i][k] + A0[k][j]) {
A0[i][j] = A0[i][k] + A0[k][j];
next[i][j] = next[i][k];
}
}
}
}
}
/**
* 打印最短路径 求顶点i到顶点j的路径
*/
public static void printTrace( int[][] next, int i, int j) {
if (next[i][j] == j) {
System. out.print((i + 1) + "" + (j + 1));
return;
}
System. out.print(i + 1);
printTrace(next, next[i][j], j);
}
public static void main(String[] args) {
// 大数来表示无穷大
int max = 1000;
int[][] A0 = { { 0, 8, 3, 1, max }, { 8, 0, 4, max, 2 },
{ 3, 4, 0, 1, 1 }, { 1, max, 1, 0, 8 }, { max, 2, 1, 8, 0 } };
int[][] next = new int[A0. length][A0. length];
/**
* 初始化next矩阵,用next矩阵存储i到j最短路径上紧跟i后的顶点 刚开始全部初始化为j
*/
for ( int i = 0; i < next. length; i++) {
for ( int j = 0; j < next. length; j++) {
next[i][j] = j;
}
}
Floyd(A0, next);
// 打印路径矩阵
for ( int i = 0; i < next. length; i++) {
for ( int j = 0; j < next. length; j++) {
printTrace(next, i, j);
System. out.print( "\t");
}
System. out.println();
}
}
}
输出结果:
11 14352 143 14 1435
25341 22 253 2534 25
341 352 33 34 35
41 4352 43 44 435
5341 52 53 534 55