【matlab】秒杀九点圆定理
三角形三边的中点,三高的垂足和三个欧拉点(连结三角形各顶点与垂心所得三线段的中点)九点共圆。
利用平面几何方法证明比较麻烦,我们利用解析几何知识,借助matlab的帮助,秒杀这道题。
说秒杀有点过,不过也已经非常快了。
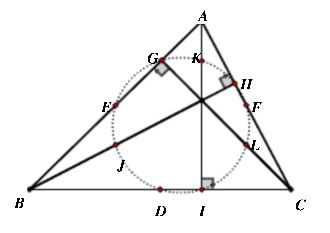
先看图。原始图片来源于网络。需要证明: G K H F L I D J E 九点共圆。
注意,图片有压缩,左边AB边上的中点是E, 右边AC的中点是F。
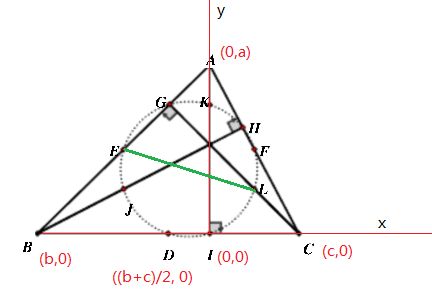
我们以 I 为原点,建立直角坐标系, 三角形三个顶点A B C,的坐标,分别计为(0, a), (b, 0), (c, 0)
a b c为三个变量。参见下图:
一个点的坐标可以用一个长度为2的数组表示,也就是一个1 * 2的矩阵,matlab天生就有矩阵运算的功能,要求两个点的中点,我们只要直接将这两个点相加再除以二即可。
注意,直线AC的斜率为 -a/c, 直线BH垂直于直线AC,根据解析几何知识,直线BH的斜率为c/a,二者的交点为垂心,坐标为
(0, -b*c/a)
输入matlab代码,得到以下点的坐标:
#先定义三个变量 syms a syms b syms c #垂心坐标 orthocenter = [0, -b*c/a] A = [0, a] B = [b, 0] C = [c, 0] I = [0, 0] D = (B + C)/2 E = (A + B)/2 F = (A + C)/2 J = (orthocenter + B)/2 L = (orthocenter + C)/2 K = (orthocenter + A)/2
还有两个点,G, H,这分别是两条直线的交点,我们需要解方程,这对matlab来说,简单的就像吃豆腐。输入以下代码:
[m,n] = solve('x/b + y/a = 1', 'b/a*(x-c) = y', 'x', 'y')
G = [m, n]
[p, q] = solve('x/c + y/a = 1', 'c/a*(x-b) = y', 'x', 'y')
H = [p, q]
solve函数中的表达式,分别是两条直线的方程。
解方程的结果如下:
G = [ b*(b*c+a^2)/(b^2+a^2), b*a*(b-c)/(b^2+a^2)] H = [ c*(b*c+a^2)/(a^2+c^2), -c*a*(b-c)/(a^2+c^2)]
接下来我们开始证明,思路如下
任意找三个点,做外接圆,然后验证其他的六个点是否在这个圆上。
添加绿色辅助线,取三角形GEL,之所以要取它,是因为这是一个直角三角形,直角三角形外接圆的圆心,就在它斜边的中点上。
外接圆的直径,就是斜边。
注意,图片被压缩,左边是E,右边是F。
外接圆的圆心我们计为 center
外接圆的半径的平方,我们计为r2,用两点间距离公式可以轻易求出。
center = (E + L)/2 tmp = E - L r2 = ( tmp(1)^2 + tmp(2)^2 )/4
tmp为两个点的差,是一个1*2的矩阵, tmp(1)为第一个元素,也即是这个点的x坐标,tmp(2)是第二个元素,也就是这个点的y坐标。
我们创建一个m文件,在里面定义一个函数,输入三个参数,第一个是一个点,第二个是圆心,第三个是半径的平方,
这个函数用来判断一个点是不是在某个圆上。
function d = is_in_cycle(p, center, r2) tmp = p - center; d = tmp(1) ^2 + tmp(2)^2 - r2
其实这就是圆的方程。返回值如果为零,表示点 p 在圆上。
接下来,只要把我们之前计算出来的点的坐标,输入到这个函数中,检查返回值即可。
比如,我们要检查点 J 是否在圆上:
ret = is_in_cycle(J, center, r2)
得到的结果是:
ret = (1/4*b-1/4*c)^2+(-1/4*b*c/a-1/4*a)^2-1/4*(1/2*b-1/2*c)^2-1/4*(1/2*a+1/2*b*c/a)^2
结果很复杂,不太容易看,不过我们有simplify函数,专门用来化简多项式:
simplify(ret) ans = 0
结果为零,这个点在圆上。
再看一个复杂的点 G,结果更加复杂,不要紧,化简!
ret = is_in_cycle(G, center, r2) ret = (b*(b*c+a^2)/(b^2+a^2)-1/4*b-1/4*c)^2+(b*a*(b-c)/(b^2+a^2)+1/4*b*c/a-1/4*a)^2-1/4*(1/2*b-1/2*c)^2-1/4*(1/2*a+1/2*b*c/a)^2 simplify(ret) ans = 0
结果为零。
逐个验证其他的点,结果全部为零。
ok,证明完毕!
解析几何解题思路简单,但是运算复杂,不过,这个复杂是对人来说的,对电脑来说,简直不值一提。
古人云,工欲善其技,必先利其器。
生产工具是生产力的主要体现,科学技术是第一生产力。
善用工具,所向无敌。