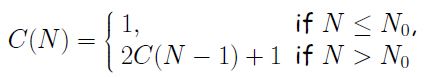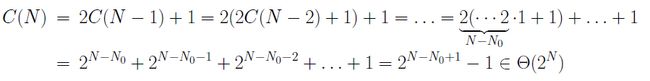算法复杂度（Algorithmic Complexity）

引言 

Cost is a principal concern throughout engineering:

“An engineer is someone who can do for a dime what any fool can do for a dollar.”

成本是整个工程的主要关注点：

工程师能只花1角钱就解决的问题，而傻子却要1美元。

Cost can mean
– Operational cost (for programs, time to run, space requirements).
– Development costs: How much engineering time? When delivered?
– Costs of failure: How robust? How safe?

成本意味着：

— 营运成本（对于程序，运行时间，存储空间）；

— 开发成本（多大的工程事件？几时可以交付使用？）；

— 失败成本（有多稳固？多安全？）。

Is this program fast enough? Depends on:
– For what purpose;
–What input data.

程序是否足够快速？这取决于：

— 为了什么目的；

— 是什么数据。

How much space (memory, disk space)?
– Again depends on what input data.

需要多少空间（内存空间，磁盘空间）？

— 也取决于是什么数据。

How will it scale, as input gets big?

当数据量变大时，规模将如何扩展？

 

举个例子

Problem: Scan a text corpus (say 107 bytes or so), and find and print the 20 most frequently used words, together with counts of how often they occur.

问题：扫描一个文本库（例如107字节左右），寻找并打印20个出现频率最多的词，并统计出现的次数。

Solution 1 (Knuth): Heavy-Duty data structures
– Hash Trie implementation, randomized placement, pointers ga-
lore, several pages long.

Solution 2 (Doug McIlroy): UNIX shell script:
tr -c -s ’[:alpha:]’ ’[\n*]’ < FILE | \
sort | \
uniq -c | \
sort -n -r -k 1,1 | \
sed 20q

方案1（Kunth）：重型数据结构

— 哈希树实现，随机放置的数据，复杂的指针，有几页长。

方案2（Doug McIlroy）：UNIX shell脚本：

tr -c -s ’[:alpha:]’ ’[\n*]’ < FILE | \
sort | \
uniq -c | \
sort -n -r -k 1,1 | \
sed 20q

Which is better?
– #1 is much faster,
– but #2 took 5 minutes to write and processes 20MB in 1 minute.
– I pick #2.

哪个比较好？

— #1比较快，

— 但#2只需要5分钟就能写好，并且能在1分钟内处理20MB的数据。

— 所以我选择#2。

In most cases, anything will do: Keep It Simple.

 

度量时间成本

Wall-clock or execution time
– You can do this at home:
time java FindPrimes 1000
– Advantages: easy to measure, meaning is obvious.
– Appropriate where time is critical (real-time systems, e.g.).
– Disadvantages: applies only to specific data set, compiler, machine, etc.

时钟或者执行时间

— 你可以在家里这么做：

　　time java FindPrimes 1000

— 好处：容易度量，简单明了

— 适于：时间是关键的地方（如：时实系统）

— 坏处：只适用于特定的数据集，编译器，机器等

Number of times certain statements are executed:
– Advantages: more general (not sensitive to speed of machine).
– Disadvantages: doesn’t tell you actual time, still applies only to specific data sets.

确定语句执行的次数：

— 好处：更为普遍（对机器速度不敏感）

— 坏处：不能告诉你实际时间，依然只适用于特定数据集

Symbolic execution times:
– That is, formulas for execution times or statement counts in terms of input size.
– Advantages: applies to all inputs, makes scaling clear.
– Disadvantage: practical formula must be approximate, may tell very little about actual time.

符号执行时间：

— 也就是，对于一个输入表达式，执行次数或者说语句数量的公式。

— 好处：可应用于所有输入，使得规模伸缩清晰明了

— 坏处：实际的公式必然是近似的，只能了解很少的实际运行时间

 

符号执行时间定义

定义1：C_r（I, P, M）为在输出为I，程序为P，机器平台为M的执行时间表达式。

定义2：C_w（N, P, M）为在最糟糕状态下的执行时间表达式：

　　　　

或许有人会说C_w（N, P, M）不是执行时间的一个好的度量方式，因为平均时间才是算法的度量标准。平均时间通常可以表示为：

　　　　

但很不幸，通常平均时间并不容易算出来。

 

数学工具

定理1：f(n)的上界可表示为：

　　　　

即可以找到一个K，使得：

　　　　f(n) <= Kg(n) ，　　当n > M时

意义：

　　1）Kg(n)是f(n)的上界

　　2）f(n)的增长速度至多与Kg(n)相同

定理2：f(n)的下界可表示为：

　　　　

即可以找到一个K，使得：

　　　　f(n) >= Kg(n)，　　当n > M时

意义：

　　1）Kg(n)是f(n)的下界

　　2）f(n)的增长速度至少与Kg(n)相同

定理3：有可能对于f(n)满足：

　　　　，又满足

　　　　

　　　　那么我们记作：

　　　　

 

 应用例子

/** 当且仅当X属于A[k]...A[A.length-1]返回true.
 * A是升序排列的，k>=0 */
static boolean isIn (int[] A, int k, int X) {
    if (k >= A.length)
        return false;
    else if (A[k] > X)
        return false;
    else if (A[k] == X)
        return true;
    else
        return isIn (A, k+1, X);
}

在最差情况下程序需要执行N次，所以：

　　　　

static void sort (int[] A) {
    for (int i = 1; i < A.length; i += 1) {
        int x = A[i];
        int j;
        for (j = i; j > 0 && x < A[j-1]; j -= 1)
            A[j] = A[j-1];
            A[j] = x;
    }
}

冒泡排序，最差情况是：

　　　　

/** 当且仅当X是S中的一个字符串返回true */
boolean occurs (String S, String X) {
    if (S.equals (X)) return true;
    if (S.length () <= X.length ()) return false;
    return
        occurs (S.substring (1), X) ||
        occurs (S.substring (0, S.length ()-1), X);
}

在最差情况下有下列递归式：

　　　　

 所以有：

　　　　

/** 当且仅当X在A[L]...A[U]中返回true
 * A是升序排列的，L>=0, U-L < A.length. */
static boolean isInB (int[] A, int L, int U, int X) {
    if (L > U)
        return false;
    else {
       int m = (L+U)/2;
       if (A[m] == X)
            return true;
       else if (A[m] > X)
            return isInB (A, L, m-1, X);
       else
            return isInB (A, m+1, U, X);
    }
}

在最差情况下有：

　　　　

 

时间成本分摊 

考虑一个二进制计数器：

0 0 0 0 0
0 0 0 0 1
0 0 0 1 0
0 0 0 1 1
0 0 1 0 0
· · ·
0 1 1 1 1
1 0 0 0 0
· · ·

在最糟糕情况下，对于N位计数器，数据变化M次有：

　　　　

但计数器实际数据增长过程，每位的花费是相关的。所以实际上总共的位变化次数为：

　　　　

可见我们可以称2次位翻转为每次计数的成本分摊。

 

对数

数学中常将lg x当成是log_e x的简写，但对于计算机科学家，lg x通常表示log₂ x，因为他们非常关注二进制有关的事情。

常用公式如下：

定理4：

　　　　

定理5：

　　　　

定理6：lg x是个增长极其缓慢的函数，我们有

　　　　

 

相关资料

Data Structures (Into Java) . Paul N. Hilfinger