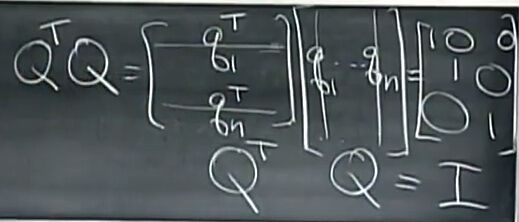
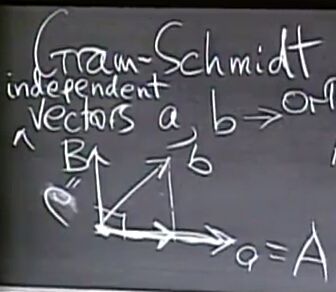
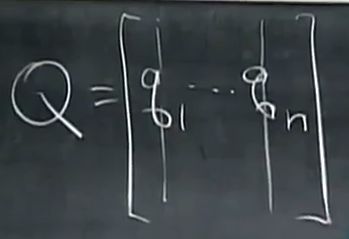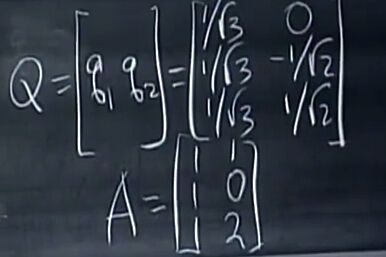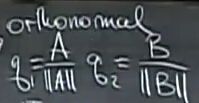- 推荐算法_隐语义-梯度下降
_feivirus_
算法机器学习和数学推荐算法机器学习隐语义
importnumpyasnp1.模型实现"""inputrate_matrix:M行N列的评分矩阵,值为P*Q.P:初始化用户特征矩阵M*K.Q:初始化物品特征矩阵K*N.latent_feature_cnt:隐特征的向量个数max_iteration:最大迭代次数alpha:步长lamda:正则化系数output分解之后的P和Q"""defLFM_grad_desc(rate_matrix,l
- 5分钟说透AppStore审核原理,让你拥有上架新思路!
Q仔本人噢
在AppStore上架是越来越难了!相信非常多公司的技术人员都为此困扰,然而外包团队水平又层次不齐,容易遇坑,实在是内忧外患。是什么原因导致审核机制频繁调整?又是什么原因使得审核变得越发严格?那么接下来听小Q分解,马上给各位带来解答!首先看一下近一年的上下架的情况:近一年上架情况近一年下架情况通过数据我们发现越是马甲包产量权重高的分类里被下架的app数量越多,苹果此举可谓是上有政策,下有对策。通过
- 2021-11-18
安安303
刘红雅中原焦点团队分享第135天筑基第4课社会心理学接上一课,心理现象。需要和动机所有的动机行为受需要的影响,现在的孩子很多方面不需要,是因为得到的太多需要使机体内部不平衡的状态,现在很多需要满足的过多,是“厌”,孩子要越用越有用,没有用到自己,自己没有价值感成就感,他就不需要开发自己的潜力。对自己和孩子的生活留白不断的学习成长,实现自己。所有有情绪的地方是触动了需求,需求没有被满足,当一个人知道
- matlab delsat = setdiff(1:69,unique(Eph(30,:))); 语句含义
黄卷青灯77
matlab开发语言setdiff
这行MATLAB代码用于计算在范围1:69中不包含在Eph矩阵第30行的唯一值集合中的所有元素。具体解释如下:delsat=setdiff(1:69,unique(Eph(30,:)));解释Eph(30,:)Eph(30,:)提取矩阵Eph的第30行的所有列元素。这是一个行向量,包含了第30行的所有值。unique(Eph(30,:))unique函数返回Eph(30,:)中的唯一元素。这意味着
- TC27x启动过程(2)-TC277
赞哥哥s
TC277学习笔记gnu单片机
接上文,继续学习TC277的启动过程。分析启动函数有关用的寄存器说明,参考文章TC27x寄存器学习目录TC27x寄存器学习start函数分析isync汇编指令(同步指令)dsync汇编指令(同步数据),1清除endinit2设置中断堆栈3启用对系统全局寄存器的写访问4初始化SDA基指针5关闭对系统全局寄存器的写访问6关闭看门狗,恢复Endinit位7初始化CSA8初始化ram,拷贝rom数据到ra
- 高级UI<第二十四篇>:Android中用到的矩阵常识
NoBugException
(1)定义在数学中,矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合。由m×n个数aij排成的m行n列的数表称为m行n列的矩阵,简称m×n矩阵。记作:图片.png这m×n个数称为矩阵A的元素,简称为元,数aij位于矩阵A的第i行第j列,称为矩阵A的(i,j)元,以数aij为(i,j)元的矩阵可记为(aij)或(aij)m×n,m×n矩阵A也记作Amn。元素是实数的矩阵称为实矩阵,元素是复
- 基于JavaWeb开发的Java+SpringMvc+vue+element实现上海汽车博物馆平台
网顺技术团队
成品程序项目javavue.js汽车课程设计springboot
基于JavaWeb开发的Java+SpringMvc+vue+element实现上海汽车博物馆平台作者主页网顺技术团队欢迎点赞收藏⭐留言文末获取源码联系方式查看下方微信号获取联系方式承接各种定制系统精彩系列推荐精彩专栏推荐订阅不然下次找不到哟Java毕设项目精品实战案例《1000套》感兴趣的可以先收藏起来,还有大家在毕设选题,项目以及论文编写等相关问题都可以给我留言咨询,希望帮助更多的人文章目录基
- 七.正则化
愿风去了
吴恩达机器学习之正则化(Regularization)http://www.cnblogs.com/jianxinzhou/p/4083921.html从数学公式上理解L1和L2https://blog.csdn.net/b876144622/article/details/81276818虽然在线性回归中加入基函数会使模型更加灵活,但是很容易引起数据的过拟合。例如将数据投影到30维的基函数上,模
- 【原创小说】总是东风错丨第十三章
郭勒的鱼
郑重声明:文章系原创非首发,首发平台:头条号,ID:郭勒的鱼,文责自负。天刚亮,府外面一片嘈杂,门被拍的山响,这一夜苏府惊魂,人们吓得如同惊弓之鸟,听到这敲门声,连苏福都不敢贸然开门。趴在门缝往外一看,是大太太的哥哥舅姥爷虞南基来了,连忙着人开门,不但是虞南基来了,还领来一队三十多个全副武装的士兵。南竹看着哥哥。嘴扁了扁,蓦然鼻子一酸哭得泣不成声,虞南基很诧异。他这个妹妹他了解,外表的柔婉其实都是
- 从单体到微服务:FastAPI ‘挂载’子应用程序的转变
黑金IT
fastapi微服务fastapi架构
在现代Web应用开发中,模块化架构是一种常见的设计模式,它有助于将大型应用程序分解为更小、更易于管理的部分。FastAPI,作为一个高性能的PythonWeb框架,提供了强大的支持来实现这种模块化设计。通过“挂载”子应用程序,我们可以为不同的功能区域(如前端接口、管理员接口和用户中心)创建独立的应用程序,并将它们整合到一个主应用程序中。本文将详细介绍如何在FastAPI中使用“挂载”子应用程序的方
- 【机器人建模和控制】读书笔记
Piccab0o
机器人
机器人建模和控制——马克·斯庞A.x10=x1∙x0x^0_1=x_1\bulletx_0x10=x1∙x0,其实就是:1)x1x_1x1轴向量在O0O_0O0系下的坐标2)在x0x_0x0轴上的投影3)坐标变换矩阵的R10R_1^0R10的第一个元素B.点p在o1x1y1z1o_1x_1y_1z_1o1x1y1z1系下的坐标p1p^1p1可以表示为:p=ux1+vy1+wz1p=ux_1+vy_
- 2023-10-16呼建荣,中原焦点团队,网络中级第33期,坚持分享734天
呼建荣
筑基课团体心理咨询技能第一讲。团体辅导、咨询、治疗的异同。1.相同:工作原理、技术、方法相似,都认为人的困惑与障碍是人与外部环境的关系出了问题,都认为可以通过团体中人际互动来解决。2.区别:①团体辅导,起源于学校,有主题,重在信息和知识的传递。人数一般在25至45人。②团体咨询,针对心理咨询,少则三五人,多则十几人到几十人。更关心团体之间的互动。重视团体动力和问题解决。③团体治疗起源于医院,6-1
- python 读写csv文件方法
菩提本无树007
pythonpandas开发语言
csv是一种结构化文件,可以将文本转化成矩阵的形式,方便程序读取和处理。下面来介绍一下使用python读写csv文件的方法:1.首先需要使用pip安装python包,然后将csv文件解压到一个文件夹下2.使用pip安装python包,安装完成后在终端输入:3.在终端输入命令:4.输入完成后,打开终端,在命令行输入以下代码:5.最后输出结果,可以看到csv文件已经打开了。6.将csv文件放入到pyt
- MATLAB语言基础教程、 小项目1:简单的计算器、 小项目2:有页面的计算器、使用App Designer创建GUI计算器
azuredragonz
学习教程matlab开发语言
MATLABMATLAB语言基础教程1.MATLAB简介2.基本语法变量与赋值向量与矩阵矩阵运算数学函数控制流3.函数4.绘图案例:简单方程求解小项目1:简单的科学计算器功能代码项目说明小项目2:有页面的计算器使用AppDesigner创建GUI计算器主要步骤:完整代码(使用MATLAB编写)说明:如何运行:小项目总结MATLAB语言基础教程1.MATLAB简介MATLAB(矩阵实验室)是一种用于
- Fork/Join框架与ForkJoinPool
浪白条
1.Fork/Join框架fork操作的作用是把一个大的问题划分成若干个较小的问题。在这个划分过程一般是递归进行的。直到可以直接进行计算。需要恰当地选取子问题的大小。太大的子问题不利于通过并行方式来提高性能,而太小的子问题则会带来较大的额外开销。每个子问题计算完成后,可以得到关于整个问题的部分解。join操作的作用是把这些分解手机组织起来,得到完整解。简单的说,ForkJoin其核心思想就是分治。
- np.identity()/np.eye()
听风1996
两个函数的原型为:np.identity(n,dtype=None)np.eye(N,M=None,k=0,dtype=);np.identity只能创建方形矩阵np.eye可以创建矩形矩阵,且k值可以调节,为1的对角线的位置偏离度,0居中,1向上偏离1,2偏离2,以此类推,-1向下偏离。值绝对值过大就偏离出去了,整个矩阵就全是0了。两者在创建单位矩阵上,并无区别,两者的区别主要在接口上;np.i
- 2022-04-04
N4一念
佛家讲世间出世间打成一片,世间即出世间,只是重点在出世间,但也不能离开世间而出世间。道家也是如此,虽然这种词语并不多。老子说:“控其锐,解其纷,和其光,同其尘'。这四句句法相同,但并不好讲。“其”指道,即道心。分解地讲道心当然代表光明,但将光明孤悬,或在深山中修道,这境界也并不很高。“和其光”的意思是把光明浑化柔和一下,就是要人勿露锋芒。“挫其锐”也是勿露锋利的意思。因此,人喜言“韬光养晦”,要人
- 图像匹配---(Python)
阳光下的Smiles
Python图像处理
图像匹配---(Python)图像匹配分为以灰度为基础的匹配和以特征为基础的匹配:(1)灰度匹配是基于像素的匹配。灰度匹配通过利用某种相似性度量,如相关函数、协方差函数、差平方和、差绝对值和等测度极值,判定两幅图像中的对应关系。(2)特征匹配则是基于区域的匹配。基于特征的匹配所处理的图像一般包含的特征有颜色特征、纹理特征、形状特征、空间位置特征等1、差分矩阵求和差分矩阵=图像A矩阵数据-图像B矩阵
- 洛谷P1719 最大加权矩形
0hang
算法c++开发语言
洛谷P1719最大加权矩形题目描述为了更好的备战NOIP2013,电脑组的几个女孩子LYQ,ZSC,ZHQ认为,我们不光需要机房,我们还需要运动,于是就决定找校长申请一块电脑组的课余运动场地,听说她们都是电脑组的高手,校长没有马上答应他们,而是先给她们出了一道数学题,并且告诉她们:你们能获得的运动场地的面积就是你们能找到的这个最大的数字。校长先给他们一个n\timesnn×n矩阵。要求矩阵中最大加
- 【编译原理】方舟编译技术课程 — 词法分析
CSU_THU_SUT
编译原理编译器编译原理llvm
打开目录阅读更佳参考视频:方舟·编译技术入门与实战以及西交冯博琴老师的相关视频编译的过程包括词法分析(分析程序符号)、语法分析(分析语法单位)、中间代码生成、代码优化和目标代码生成。一、编译过程各部分的任务(1)词法分析:输入源程序,扫描分解源程序字符串,识别五类符号,包括定义符、标识符、运算符、界符和常数,转为单词符号。(2)语法分析:在词法分析基础上,将单词符号转为语法单位(如短句、子句、句子
- 4×4矩阵键盘详解(STM32)
辰哥单片机设计
STM32传感器教学矩阵计算机外设stm32嵌入式硬件单片机传感器
目录一、介绍二、传感器原理1.原理图2.工作原理介绍三、程序设计main.c文件button4_4.h文件button4_4.c文件四、实验效果五、资料获取项目分享一、介绍矩阵键盘,又称为行列式键盘,是用4条I/O线作为行线,4条I/O线作为列线组成的键盘。在行线和列线的每一个交叉点上设置一个按键,因此键盘中按键的个数是4×4个。这种行列式键盘结构能够有效地提高单片机系统中I/O口的利用率,节约单
- 【 日本鲫鱼钓 】浮游矶钓不同目标鱼不同钓法,日本专业矶钓书籍
夏说钓鱼
夏说钓鱼,聊海外钓鱼,助钓友钓技!浮游矶钓不同目标鱼不同钓法,翻译来自《日本図解釣り入門基礎から始める海のウキ釣り入門》说到浮钓,由于它的目标鱼类多种多样,因此针对不同类型的目标也会有不同的浮钓方式。下面介绍一下同种类的浮钓方法和目标鱼类。【伸缩竿的小型钓法】用4.5~5.3米的伸缩竿的钓鱼方法。与矶钓竿相比,这种钓鱼竿更加轻便,连儿童也可以使用。目标鱼类有鲰虎鱼、海鲫、沙氏下鱲、竹荚鱼、鲪鱼、小
- 抖音开始怎么吸粉(可以试试这几种办法)
配音新手圈
如何在抖音短视频平台上快速积累人气和粉丝,抖音短视频平台已成为“我们媒体”和全媒体矩阵,是客户获取、推广和收入的重要平台之一。兼职副业推荐公众号,配音新手圈,声优配音圈,新配音兼职圈,配音就业圈,鼎音副业,有声新手圈,每天更新各种远程工作与在线兼职,职位包括:写手、程序开发、剪辑、设计、翻译、配音、无门槛、插画、翻译、等等。。。每日更新兼职。但对于初学者来说,如何在抖音上建立自己的品牌,积累粉丝,
- 系统架构设计师教程 第5章 5.3 系统分析与设计 笔记
z2014z
系统架构设计师系统架构笔记
5.3系统分析与设计系统分析阶段把复杂的对象分解为简单的组成部分,其基本任务是在充分了解用户需求的基础上,书写系统需求规格说明书。系统设计是根据系统分析的结果,完成系统的构建过程。其主要目的是绘制系统的蓝图,权衡和比较各种技术和实施方法的利弊,合理分配各种资源,构建新系统的详细设计方案和相关模型,指导系统实施工作的顺利开展。系统设计的主要内容包括概要设计和详细设计。5.3.1结构化方法★★★★★针
- nfs服务搭建
GHope
nfs是什么?基哥度娘网络文件系统(NFS)是sun微系统最初开发的分布式文件系统协议,[1]允许客户端计算机上的用户通过计算机网络访问文件很像本地存储被访问。NFS与许多其他协议一样,在开放网络计算远程过程调用(很久以前RPC)系统上建立。NFS是在请求注释(RFC)中定义的开放标准,允许任何人实现协议。NFSNFS优势:节省本地存储空间,将常用的数据存放在一台NFS服务器上且可以通过网络访问,
- 云服务业界动态简报-20180128
Captain7
一、青云青云QingCloud推出深度学习平台DeepLearningonQingCloud,包含了主流的深度学习框架及数据科学工具包,通过QingCloudAppCenter一键部署交付,可以让算法工程师和数据科学家快速构建深度学习开发环境,将更多的精力放在模型和算法调优。二、腾讯云1.腾讯云正式发布腾讯专有云TCE(TencentCloudEnterprise)矩阵,涵盖企业版、大数据版、AI
- 数据分析-24-时间序列预测之基于keras的VMD-LSTM和VMD-CNN-LSTM预测风速
皮皮冰燃
数据分析数据分析
文章目录1普通的LSTM模型1.1数据重采样1.2数据标准化1.3切分窗口1.4划分数据集1.5建立模型1.6预测效果2VMD-LSTM模型2.1VMD分解时间序列2.2对每一个IMF建立LSTM模型2.2.1IMF1—LSTM2.2.2IMF2-LSTM2.2.3统一代码2.3评估效果3CNN-LSTM模型3.1数据预处理3.2建立模型3.3效果预测4VMD-CNN-LSTM模型4.1VMD分解
- 中原焦点团队张俊功初24、中24持续分享第319天 挑战约练第七期第组周第1次共9次,总计54次(2021.12.7)
5d4750373a7c
筑基第十五讲:复听:尊重:确认来访者知觉就是最大的尊重。尊重是一视同仁的,共情是因人而异的。在他的世界他是对的。关注到人本身,而不是关注问题。尊重的意义:建立良好关系的基础。尊重也是一种信任。无条件的接纳。接纳未知欣赏好奇。平等。无条件接纳:接纳是接纳他的情感而非认同他的行为。接纳并非对恶习无动于衷。具体化:时间、地点、人物、事件、感受、重要他人…顺势而为,镜中花水中月。助人之前先敲敲门。和孩子相
- JavaScript 基础 - 第13天
+码农快讯+
JavaScript学习笔记javascript开发语言ecmascript
文章目录JavaScript基础-第13天深入对象创建对象三种方式构造函数new实例化过程实例成员&静态成员实例成员静态成员一切皆对象内置构造函数ObjectArrayStringNumberJavaScript基础-第13天了解面向对象编程的基础概念及构造函数的作用,体会JavaScript一切皆对象的语言特征,掌握常见的对象属性和方法的使用。深入对象内置构造函数综合案例深入对象了解面向对象的基
- 十二个养生小知识汇总集(九)
营养师茶茶
一、多吃浆果类水果,可以帮助延缓大脑衰老研究显示:每周至少吃一份蓝莓、两份草莓的女性与那些不吃浆果的女性相比,认知功能减退的速度至少延缓了两年这些结果显示,每天吃一把浆果这样一个简单又美味的饮食调整,就能把大脑的老化速度,至少往后推迟两年。就算只喝果蔬汁,也可能对身体有好处浆果类水果富含抗氧化剂,能够帮助清楚大脑的自由基,避免大脑的氧化损伤,所以平时尽量多吃一些,好处多多二、女人建议平常多吃一些醋
- [黑洞与暗粒子]没有光的世界
comsci
无论是相对论还是其它现代物理学,都显然有个缺陷,那就是必须有光才能够计算
但是,我相信,在我们的世界和宇宙平面中,肯定存在没有光的世界....
那么,在没有光的世界,光子和其它粒子的规律无法被应用和考察,那么以光速为核心的
&nbs
- jQuery Lazy Load 图片延迟加载
aijuans
jquery
基于 jQuery 的图片延迟加载插件,在用户滚动页面到图片之后才进行加载。
对于有较多的图片的网页,使用图片延迟加载,能有效的提高页面加载速度。
版本:
jQuery v1.4.4+
jQuery Lazy Load v1.7.2
注意事项:
需要真正实现图片延迟加载,必须将真实图片地址写在 data-original 属性中。若 src
- 使用Jodd的优点
Kai_Ge
jodd
1. 简化和统一 controller ,抛弃 extends SimpleFormController ,统一使用 implements Controller 的方式。
2. 简化 JSP 页面的 bind, 不需要一个字段一个字段的绑定。
3. 对 bean 没有任何要求,可以使用任意的 bean 做为 formBean。
使用方法简介
- jpa Query转hibernate Query
120153216
Hibernate
public List<Map> getMapList(String hql,
Map map) {
org.hibernate.Query jpaQuery = entityManager.createQuery(hql);
if (null != map) {
for (String parameter : map.keySet()) {
jp
- Django_Python3添加MySQL/MariaDB支持
2002wmj
mariaDB
现状
首先,
[email protected] 中默认的引擎为 django.db.backends.mysql 。但是在Python3中如果这样写的话,会发现 django.db.backends.mysql 依赖 MySQLdb[5] ,而 MySQLdb 又不兼容 Python3 于是要找一种新的方式来继续使用MySQL。 MySQL官方的方案
首先据MySQL文档[3]说,自从MySQL
- 在SQLSERVER中查找消耗IO最多的SQL
357029540
SQL Server
返回做IO数目最多的50条语句以及它们的执行计划。
select top 50
(total_logical_reads/execution_count) as avg_logical_reads,
(total_logical_writes/execution_count) as avg_logical_writes,
(tot
- spring UnChecked 异常 官方定义!
7454103
spring
如果你接触过spring的 事物管理!那么你必须明白 spring的 非捕获异常! 即 unchecked 异常! 因为 spring 默认这类异常事物自动回滚!!
public static boolean isCheckedException(Throwable ex)
{
return !(ex instanceof RuntimeExcep
- mongoDB 入门指南、示例
adminjun
javamongodb操作
一、准备工作
1、 下载mongoDB
下载地址:http://www.mongodb.org/downloads
选择合适你的版本
相关文档:http://www.mongodb.org/display/DOCS/Tutorial
2、 安装mongoDB
A、 不解压模式:
将下载下来的mongoDB-xxx.zip打开,找到bin目录,运行mongod.exe就可以启动服务,默
- CUDA 5 Release Candidate Now Available
aijuans
CUDA
The CUDA 5 Release Candidate is now available at http://developer.nvidia.com/<wbr></wbr>cuda/cuda-pre-production. Now applicable to a broader set of algorithms, CUDA 5 has advanced fe
- Essential Studio for WinRT网格控件测评
Axiba
JavaScripthtml5
Essential Studio for WinRT界面控件包含了商业平板应用程序开发中所需的所有控件,如市场上运行速度最快的grid 和chart、地图、RDL报表查看器、丰富的文本查看器及图表等等。同时,该控件还包含了一组独特的库,用于从WinRT应用程序中生成Excel、Word以及PDF格式的文件。此文将对其另外一个强大的控件——网格控件进行专门的测评详述。
网格控件功能
1、
- java 获取windows系统安装的证书或证书链
bewithme
windows
有时需要获取windows系统安装的证书或证书链,比如说你要通过证书来创建java的密钥库 。
有关证书链的解释可以查看此处 。
public static void main(String[] args) {
SunMSCAPI providerMSCAPI = new SunMSCAPI();
S
- NoSQL数据库之Redis数据库管理(set类型和zset类型)
bijian1013
redis数据库NoSQL
4.sets类型
Set是集合,它是string类型的无序集合。set是通过hash table实现的,添加、删除和查找的复杂度都是O(1)。对集合我们可以取并集、交集、差集。通过这些操作我们可以实现sns中的好友推荐和blog的tag功能。
sadd:向名称为key的set中添加元
- 异常捕获何时用Exception,何时用Throwable
bingyingao
用Exception的情况
try {
//可能发生空指针、数组溢出等异常
} catch (Exception e) {
- 【Kafka四】Kakfa伪分布式安装
bit1129
kafka
在http://bit1129.iteye.com/blog/2174791一文中,实现了单Kafka服务器的安装,在Kafka中,每个Kafka服务器称为一个broker。本文简单介绍下,在单机环境下Kafka的伪分布式安装和测试验证 1. 安装步骤
Kafka伪分布式安装的思路跟Zookeeper的伪分布式安装思路完全一样,不过比Zookeeper稍微简单些(不
- Project Euler
bookjovi
haskell
Project Euler是个数学问题求解网站,网站设计的很有意思,有很多problem,在未提交正确答案前不能查看problem的overview,也不能查看关于problem的discussion thread,只能看到现在problem已经被多少人解决了,人数越多往往代表问题越容易。
看看problem 1吧:
Add all the natural num
- Java-Collections Framework学习与总结-ArrayDeque
BrokenDreams
Collections
表、栈和队列是三种基本的数据结构,前面总结的ArrayList和LinkedList可以作为任意一种数据结构来使用,当然由于实现方式的不同,操作的效率也会不同。
这篇要看一下java.util.ArrayDeque。从命名上看
- 读《研磨设计模式》-代码笔记-装饰模式-Decorator
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
import java.io.BufferedOutputStream;
import java.io.DataOutputStream;
import java.io.FileOutputStream;
import java.io.Fi
- Maven学习(一)
chenyu19891124
Maven私服
学习一门技术和工具总得花费一段时间,5月底6月初自己学习了一些工具,maven+Hudson+nexus的搭建,对于maven以前只是听说,顺便再自己的电脑上搭建了一个maven环境,但是完全不了解maven这一强大的构建工具,还有ant也是一个构建工具,但ant就没有maven那么的简单方便,其实简单点说maven是一个运用命令行就能完成构建,测试,打包,发布一系列功
- [原创]JWFD工作流引擎设计----节点匹配搜索算法(用于初步解决条件异步汇聚问题) 补充
comsci
算法工作PHP搜索引擎嵌入式
本文主要介绍在JWFD工作流引擎设计中遇到的一个实际问题的解决方案,请参考我的博文"带条件选择的并行汇聚路由问题"中图例A2描述的情况(http://comsci.iteye.com/blog/339756),我现在把我对图例A2的一个解决方案公布出来,请大家多指点
节点匹配搜索算法(用于解决标准对称流程图条件汇聚点运行控制参数的算法)
需要解决的问题:已知分支
- Linux中用shell获取昨天、明天或多天前的日期
daizj
linuxshell上几年昨天获取上几个月
在Linux中可以通过date命令获取昨天、明天、上个月、下个月、上一年和下一年
# 获取昨天
date -d 'yesterday' # 或 date -d 'last day'
# 获取明天
date -d 'tomorrow' # 或 date -d 'next day'
# 获取上个月
date -d 'last month'
#
- 我所理解的云计算
dongwei_6688
云计算
在刚开始接触到一个概念时,人们往往都会去探寻这个概念的含义,以达到对其有一个感性的认知,在Wikipedia上关于“云计算”是这么定义的,它说:
Cloud computing is a phrase used to describe a variety of computing co
- YII CMenu配置
dcj3sjt126com
yii
Adding id and class names to CMenu
We use the id and htmlOptions to accomplish this. Watch.
//in your view
$this->widget('zii.widgets.CMenu', array(
'id'=>'myMenu',
'items'=>$this-&g
- 设计模式之静态代理与动态代理
come_for_dream
设计模式
静态代理与动态代理
代理模式是java开发中用到的相对比较多的设计模式,其中的思想就是主业务和相关业务分离。所谓的代理设计就是指由一个代理主题来操作真实主题,真实主题执行具体的业务操作,而代理主题负责其他相关业务的处理。比如我们在进行删除操作的时候需要检验一下用户是否登陆,我们可以删除看成主业务,而把检验用户是否登陆看成其相关业务
- 【转】理解Javascript 系列
gcc2ge
JavaScript
理解Javascript_13_执行模型详解
摘要: 在《理解Javascript_12_执行模型浅析》一文中,我们初步的了解了执行上下文与作用域的概念,那么这一篇将深入分析执行上下文的构建过程,了解执行上下文、函数对象、作用域三者之间的关系。函数执行环境简单的代码:当调用say方法时,第一步是创建其执行环境,在创建执行环境的过程中,会按照定义的先后顺序完成一系列操作:1.首先会创建一个
- Subsets II
hcx2013
set
Given a collection of integers that might contain duplicates, nums, return all possible subsets.
Note:
Elements in a subset must be in non-descending order.
The solution set must not conta
- Spring4.1新特性——Spring缓存框架增强
jinnianshilongnian
spring4
目录
Spring4.1新特性——综述
Spring4.1新特性——Spring核心部分及其他
Spring4.1新特性——Spring缓存框架增强
Spring4.1新特性——异步调用和事件机制的异常处理
Spring4.1新特性——数据库集成测试脚本初始化
Spring4.1新特性——Spring MVC增强
Spring4.1新特性——页面自动化测试框架Spring MVC T
- shell嵌套expect执行命令
liyonghui160com
一直都想把expect的操作写到bash脚本里,这样就不用我再写两个脚本来执行了,搞了一下午终于有点小成就,给大家看看吧.
系统:centos 5.x
1.先安装expect
yum -y install expect
2.脚本内容:
cat auto_svn.sh
#!/bin/bash
- Linux实用命令整理
pda158
linux
0. 基本命令 linux 基本命令整理
1. 压缩 解压 tar -zcvf a.tar.gz a #把a压缩成a.tar.gz tar -zxvf a.tar.gz #把a.tar.gz解压成a
2. vim小结 2.1 vim替换 :m,ns/word_1/word_2/gc
- 独立开发人员通向成功的29个小贴士
shoothao
独立开发
概述:本文收集了关于独立开发人员通向成功需要注意的一些东西,对于具体的每个贴士的注解有兴趣的朋友可以查看下面标注的原文地址。
明白你从事独立开发的原因和目的。
保持坚持制定计划的好习惯。
万事开头难,第一份订单是关键。
培养多元化业务技能。
提供卓越的服务和品质。
谨小慎微。
营销是必备技能。
学会组织,有条理的工作才是最有效率的。
“独立
- JAVA中堆栈和内存分配原理
uule
java
1、栈、堆
1.寄存器:最快的存储区, 由编译器根据需求进行分配,我们在程序中无法控制.2. 栈:存放基本类型的变量数据和对象的引用,但对象本身不存放在栈中,而是存放在堆(new 出来的对象)或者常量池中(字符串常量对象存放在常量池中。)3. 堆:存放所有new出来的对象。4. 静态域:存放静态成员(static定义的)5. 常量池:存放字符串常量和基本类型常量(public static f