RGB图像转为灰度图
最后结论:
Grey = (R*38 + G*75 + B*15)>> 7
代码
#include <cv.h>
#include <highgui.h>
using namespace cv;
int main(){
Mat src= imread("C:\\Users\\Poplar\\Pictures\\ff.jpg");
Mat grey(src.rows, src.cols, CV_8UC1, Scalar(0));
for (inty = 0; y < src.rows; y++)
{
uchar*cp = src.ptr<uchar>(y);
uchar*gp = grey.ptr<uchar>(y);
for(int x = 0; x < src.cols; x++){
*gp= (15*cp[0] + 75*cp[1] + 38*cp[2]) >> 7;
cp+= 3;
gp++;
}
}
imshow("src",src);
imshow("grey",grey);
waitKey(0);
return0;
}
效果如图
下面具体解释
RGB彩色图像中,一种彩色由R(红色),G(绿色),B(蓝色)三原色按比例混合而成。
图像的基本单元是一个像素,就像一个巨幅电子广告屏上远处看是衣服图像,走近你会看到一个一个的方格,这个方格的颜色是一种,从远处看,觉察不到这个方格的存在。
一个像素需要3块表示,分别代表R,G,B,如果8为表示一个颜色,就由0-255区分不同亮度的某种原色。
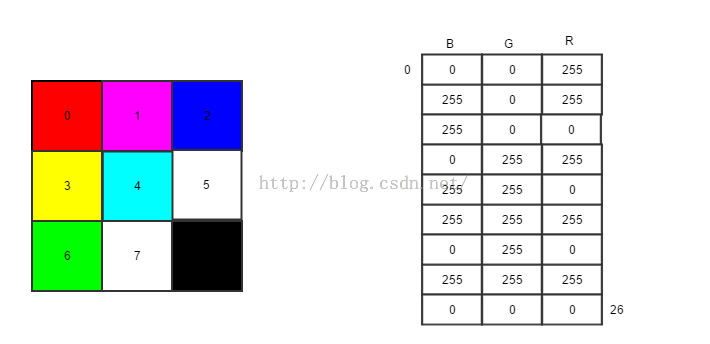
一张9像素的8位RGB图像,在计算机内存中的分布大概示意如下:
实际中数都是二进制形式的,并且未必按照R,G,B顺序,比如opencv是按照B,G,R顺序将三个色值保存在3个连续的字节里
灰度图像是用不同饱和度的黑色来表示每个图像点,比如用8位 0-255数字表示“灰色”程度,每个像素点只需要一个灰度值,8位即可,这样一个3X3的灰度图,只需要9个byte就能保存
RGB值和灰度的转换,实际上是人眼对于彩色的感觉到亮度感觉的转换,这是一个心理学问题,有一个公式:
Grey = 0.299*R + 0.587*G + 0.114*B
根据这个公式,依次读取每个像素点的R,G,B值,进行计算灰度值(转换为整型数),将灰度值赋值给新图像的相应位置,所有像素点遍历一遍后完成转换。
一张500X500的图像转换为同样大小的灰度图需要进行25万次上述公式的计算。进行优化是很有必要的,这个简单的算法是O(n)复杂度的,应该是不能优化了(或者用并行进行优化,本文不涉及),但是Grey = 0.299*R + 0.587*G + 0.114*B有更加高效的等价形式。
在ALU中,位操作快于整数加法,整数加法快于整数乘法(快多少取决于有没有乘法电路,乘法电路的结构),整数运算又比浮点数运算快得多。
所以可以通过将浮点数运算转化为整数运算,整数运算转换为位操作进行优化
Grey = 0.299*R + 0.587*G + 0.114*B
可以转化为
Grey = (299*R + 587*G + 114*B + 500) /1000;
整数运算会截断小数部分,加上500是为了四舍五入(找两个例子便可理解),减少精度损失。
这里的除法/ 即使是整数除法计算也是很耗时,转换为移位操作可以优化,那么怎么转换为位操作?左右移位对应于乘除2的幂,为了把除法转为右移操作,做如下处理:
Grey = 0.299*R + 0.587*G + 0.114*B
Grey = (299*R+ 587*G + 114*B)÷ 1000
Grey = (1024*299*R+ 1024*587*G + 1024*114*B)÷(1024*1000)
Grey = (306176*R+601088*G + 116736*B)÷(1024*1000)
Grey = (306.176*R+601.088*G + 116.736*B)÷(1024)
Grey = (306*R+601*G + 116*B)÷(1024)//截断误差
Grey = (306*R+601*G + 116*B) >> 10;
误差最大是多少?
(0.176*255+0.088*255 + 0.736*255) ÷1024 = 255÷1024=0.249,可能会导致1个灰度值的波动
有一种计算方法可以降低误差
R 的系数 =1024*0.229= 306.176≈306
G的系数 =1024*0.587 + 0.176 =601.264 ≈601
B的系数 =1024*0.114 + 0.264 = 117
保留了小数部分的作用,可以得到一个误差较小的公式:
Grey = (306*R +601*G + 117*B) >> 10;
这样得来的是10位精度的。
同样的方法可以获得其他精度的,比如
Grey = (R*1 + G*2 + B*1) >> 2 ( Grey = (R + G<<1 + B) >> 2 )
Grey= (R*38 + G*75 + B*15) >> 7
Grey= (R*76 + G*150 + B*30) >> 8
Grey = (R*19595 + G*38469 + B*7472) >> 16
可以看出来,7位和8位精度是一样的,比较好用的是7位精度的公式。
实际编写代码时,还要考虑图像文件的读取问题,不同格式的RGB位图,结构不同,读取时也不同,本文不涉及图像读取问题,这里以openCV提供的图像读取方式,展示转灰度图的实际代码,见文章开头。
2-10位精度的公式
Grey = (R*1 + G*2 + B*1) >> 2
Grey= (R*2 + G*5 + B*1) >> 3
Grey= (R*4 + G*10 + B*2) >> 4
Grey = (R*9 + G*19 + B*4) >> 5
Grey = (R*19 + G*37 + B*8) >> 6
Grey= (R*38 + G*75 + B*15) >> 7
Grey= (R*76 + G*150 + B*30) >> 8
Grey = (R*153 + G*300 + B*59) >> 9
Grey = (R*306 + G*601 + B*117) >> 10
Grey = (R*612 + G*1202 + B*234) >> 11
Grey = (R*1224 + G*2405 + B*467) >> 12
Grey= (R*2449 + G*4809 + B*934) >> 13
Grey= (R*4898 + G*9618 + B*1868) >> 14
Grey = (R*9797 + G*19235 + B*3736) >> 15
Grey = (R*19595 + G*38469 + B*7472) >> 16
Grey = (R*39190 + G*76939 + B*14943) >> 17
Grey = (R*78381 + G*153878 + B*29885) >> 18
Grey =(R*156762 + G*307757 + B*59769) >> 19
Grey= (R*313524 + G*615514 + B*119538) >> 20