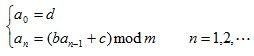0041算法笔记——【随机化算法】随机化算法与随机数问题

     1、随机化算法

    (1)描述：随机化算法是这样一种算法，在算法中使用了随机函数，且随机函数的返回值直接或者间接的影响了算法的执行流程或执行结果。随机化算法基于随机方法，依赖于概率大小。

    (2)分类：一般情况下，可将概率（随机化）算法大致分为四类:数值概率算法，蒙特卡罗（Monte Carlo）算法，拉斯维加斯（Las Vegas）算法和舍伍德（Sherwood）算法。

    数值随机化算法：数值概率算法常用于数值问题的求解。这类算法所得到的往往是近似解。而且近似解的精度随计算时间的增加不断提高。在许多情况下，要计算出问题的精确解是不可能或没有必要的，因此用数值概率算法可得到相当满意的解。

    蒙特卡罗（Monte Carlo）算法：蒙特卡罗（Monte Carlo）算法用于求问题的准确解。用蒙特卡罗算法能求得问题的一个解，但这个解未必是正确的。求得正确解的概率依赖于算法所用的时间。算法所用的时间越多，得到正确解的概率就越高。蒙特卡罗算法的主要缺点就在于此。一般情况下，无法有效判断得到的解是否肯定正确。

    拉斯维加斯（Las Vegas）算法：拉斯维加斯（Las Vegas）算法不会得到不正确的解，一旦用拉斯维加斯算法找到一个解，那么这个解肯定是正确的。但是有时候用拉斯维加斯算法可能找不到解。与蒙特卡罗算法类似。拉斯维加斯算法得到正确解的概率随着它用的计算时间的增加而提高。对于所求解问题的任一实例，用同一拉斯维加斯算法反复对该实例求解足够多次，可使求解失效的概率任意小。

    舍伍德（Sherwood）算法：舍伍德（Sherwood）算法总能求得问题的一个解，且所求得的解总是正确的。当一个确定性算法在最坏情况下的计算复杂性与其在平均情况下的计算复杂性有较大差别时，可以在这个确定算法中引入随机性将它改造成一个舍伍德算法，消除或减少问题的好坏实例间的这种差别。舍伍德算法精髓不是避免算法的最坏情况行为，而是设法消除这种最坏行为与特定实例之间的关联性。这意味着不存在坏的输入，只有坏的随机数。

    2、随机数

    随机数在随机化算法设计中扮演着十分重要的角色。在现实计算机上无法产生真正的随机数，因此在随机化算法中使用的随机数都是一定程度上随机的，即伪随机数。
线性同余法是产生伪随机数的最常用的方法。由线性同余法产生的随机序列a0,a1,…,an满足：

     其中b>=0，c>=0，d<=m。d称为该随机序列的种子。如何选取该方法中的常数b、c和m直接关系到所产生的随机序列的随机性能。从直观上看，m应取得充分大，因此可取m为机器大数，另外应取gcd(m,b)=1，因此可取b为一素数。

     利用线性同余法原理，可以设计出一个随机数类RandomNumber。该类包含一个由用户初始化的种子randSeed。给定初始种子后，即可产生与之相对应的随机序列。种子randSeed是一个无符号整型数，可由用户选定也可用系统时间自动产生。函数Random在每次计算时，用线性同余式计算新的种子randSeed。它的高16位的随机性较好。将randSeed右移16位得到一个0~65535间的随机整数。然后将此随机数映射到0~(n-1)范围内。函数fRandom,先用函数Random(maxshort)产生一个0~(maxshot-1)之间的整型随机序列，将每个整型随机数除以maxshort，就得到[0,1)区间中的随机实数。具体代码如下：

#include"time.h"
//随机数类
const unsigned long maxshort = 65536L;
const unsigned long multiplier = 1194211693L;
const unsigned long adder = 12345L;

class RandomNumber
{
	private:
		//当前种子
		unsigned long randSeed;
	public:
		RandomNumber(unsigned long s = 0);//构造函数，默认值0表示由系统自动产生种子
		unsigned short Random(unsigned long n);//产生0：n-1之间的随机整数
		double fRandom(void);//产生[0,1)之间的随机实数
};

RandomNumber::RandomNumber(unsigned long s)//产生种子
{
	if(s == 0)
	{
		randSeed = time(0);//用系统时间产生种子
	}
	else
	{
		randSeed = s;//由用户提供种子
	}
}

unsigned short RandomNumber::Random(unsigned long n)//产生0：n-1之间的随机整数
{
	randSeed = multiplier * randSeed + adder;//线性同余式
	return (unsigned short)((randSeed>>16)%n);
}

double RandomNumber::fRandom(void)//产生[0,1)之间的随机实数
{
	return Random(maxshort)/double(maxshort);
}

    3、随机数测试

    用计算机产生的伪随机数来模拟抛硬币试验。假设抛10次硬币，每次抛硬币得到正面和反面是随机的。拋10次硬币构成一个事件。调用Random(2)返回一个二值结果。在主程序中反复调用函数TossCoins模拟拋10次硬币这一事件50000次。用head[i](0<=i<=10)记录这50000次模拟恰好得到i次正面的刺手。最终输出模拟抛硬币事件得到的正面事件的概率图。具体代码如下：

//随机数类抛硬币实验测试
#include "stdafx.h"
#include "RandomNumber.h"
#include <iostream>
using namespace std;

int TossCoins(int numberCoins);

int main()
{
	//模拟随机抛硬币事件
	const int NCOINS = 10;
	const long NTOSSES = 50000L;
	//heads[i]是得到i次正面的次数
	long i,heads[NCOINS+1];

	int j,position;

	//初始化数组heads
	for(int j=0; j<NCOINS+1;j++)
	{
		heads[j] = 0;
	}

	//重复50,000次模拟事件
	for(int i=0; i<NTOSSES; i++)
	{
		heads[TossCoins(NCOINS)]++;
	}

	//输出频率图
	for(int i=0; i<=NCOINS; i++)
	{
		position = int(float(heads[i])/NTOSSES*72);
		cout<<i<<" ";
		for(int j=0; j<position-1; j++)
		{
			cout<<" ";
		}
		cout<<"*"<<endl;
	}

	return 0;
}

int TossCoins(int numberCoins)
{
	//随机抛硬币
	static RandomNumber coinToss;
	int i,tosses = 0;
	for(int i=0; i<numberCoins; i++)
	{
		//Random(2) = 1表示正面
		tosses += coinToss.Random(2);
	}
	return tosses;
}

    程序运行结果如图：