有限状态机
1 定义
有限状态机(finite-state machine, FSM),又称有限状态自动机,简称状态机,是表示有限个状态以及在这些状态之间的转移和动作等行为的数学模型。
2 概念和术语
状态存储关于过去的信息,就是说:它反映从系统开始到现在时刻的输入变化。
转移指示状态变更,并且用必须满足来确使转移发生的条件来描述它。
动作是在给定时刻要进行的活动的描述。有多种类型的动作:
l 进入动作:在进入状态时进行
l 退出动作:在退出状态时进行
l 输入动作:依赖于当前状态和输入条件进行
l 转移动作:在进行特定转移时进行
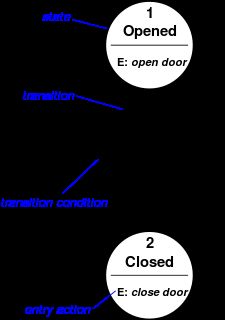
图1 开关门状态图
FSM(有限状态机)可以使用上面图 1 那样的状态图来表示,此外还可以使用多种类型的状态转移表。下面展示最常见的表示:当前状态(B)和条件(Y)的组合指示出下一个状态(C)。完整的动作信息可以只使用脚注来增加。
| 状态转移表 |
|||
| 当前状态 → |
状态 A |
状态 B |
状态 C |
| 条件 X |
… |
… |
… |
| 条件 Y |
… |
状态 C |
… |
| 条件 Z |
… |
… |
… |
除了建模这里介绍的反应系统之外,有限状态自动机在很多不同领域中是重要的,包括电子工程、 语言学、计算机科学、哲学、生物学、数学和逻辑学。有限状态机是在自动机理论和计算理论中研究的一类自动机。在计算机科学中,有限状态机被广泛用于建模应用行为、硬件电路系统设计、软件工程,编译器、网络协议、和计算与语言的研究。
3 分类
有限状态机有两个不同的群组:接受器/识别器和变换器。
3.1 接受器和识别器
图2 接受器 FSM:解析单词"nice"
接受器和识别器(也叫做序列检测器)产生一个二元输出,说要么“是”要么“否”来回答输入是否被机器接受。所有FSM的状态被称为要么接受要么不接受。在所有输入都被处理了的时候,如果当前状态是接受状态,输入被接受,否则被拒绝。图2中的例子展示了接受单词 "nice"的有限状态机。
3.1.1 开始状态
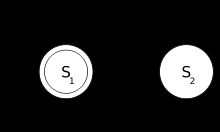
开始状态通常用“没有起点的箭头”指向它来表示,如图3左边的圆。
3.1.2 接受状态
接受状态是机器符合了设定条件后的状态,它通常表示为双重圆圈。如图3左边的圆,它确定二进制输入是否包含偶数个 0,S1(它也是开始状态)指示已经输入了偶数个0的状态。
图3一个检测二进制数具有奇数或者偶数个0的状态机
3.2 变换器
变换器基于当前状态和输入生成输出。它们用于控制应用。常分为两种类型:Moore机和Mealy机。
3.2.1 Moore机
摩尔型有限状态机(Moore machine)是只使用进入动作的有限状态机,就是说输出只依赖于状态。Moore 模型的好处是行为的简单性。
图1的例子展示了一个电梯门的Moore机。这个状态机识别两个命令:“command_open”和“command_close”。在状态“Opening”中的进入动作 (E: Opendoor)开启电机开门,在状态“Closing”中的进入动作以反方向开启电机关门。它们通知外部世界(比如其他状态机)情况:“门开着”或“门关着”。
3.2.2 Mealy机
米利型有限状态机(Mealy machine)是基于它的当前状态和输入生成输出的有限状态自动机(更精确的叫有限状态变换器)。与输出只依赖于机器当前状态的摩尔有限状态机不同,它的输出与当前状态和输入都有关。
图4 变换器FSM:Mealy 模型例子
只使用输入动作的FSM,就是说输出依赖于输入和状态。Mealy机的使用经常导致状态数目的简约。在图4中的例子展示了实现同上面 Moore 机同样行为的Mealy 机。有两个输入动作(I:):“开启电机关门如果 command_close 下达”和“反向开启电机开门如果 command_open 下达”。