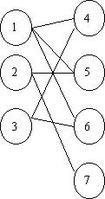
二分图
什么是二分图
二分图又称作二部图,是图论中的一种特殊模型。设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集
(X,Y),并且图中的每条边(i,j)
关联的两个顶点i和j分别属于这两个不同的顶点集X和 Y , 则称图G为一个二分图。
什么是最大匹配
给定一个二分图G,在G的一个子图M中,M的边集中的任意两条边都不依附于同一个顶点,则称M是一个匹配.
选择这样的边数最大的子集称为图的最大匹配问题(maximalmatching problem)
如果一个匹配中,图中的每个顶点都和图中某条边相关联,则称此匹配为完全匹配,也称作完美匹配.
同时二分图最大匹配问题又可以转化成“最小顶点覆盖”、“最小路径覆盖”、“最大独立集“等问题
匈牙利算法求二分图的最大匹配
算法的核心思想是由一个初始匹配不断找增广路,直到找不到增广路为止。这里的增广路和网络流中的增广路有些不同。这里的增广路是这样的一条路:设已有的匹配为M,它的第一条边不在M中,最后一条边也不在M中,中间为在M中的边与不在M中的边交错出现。显然,这条路起点在X中,终点在Y中,且不在M中的边比在M中的边多1。所以我们若对增广路中的边进行取反,即原来不是匹配边的边变为匹配边,原来是匹配边的边变为不是匹配边的边,则我们能获得一个更大的匹配。所以这么一直找下去,直到找不到增广路为止,我们最后得到的匹配M就是要求的最大匹配。
1 匈牙利算法中,初始匹配我们可以设为空,然后用DFS或者BFS找增广路。找一条增广路的复杂度为O(E),最多找V条增广路,故算法时间复杂度为O(VE)。
2 只要有找到增广路,就让ans++,为什么呢,因为一条增广路总是有未匹配的边比匹配边多1,那么如果取反后就相当与匹配边多1,那么就是ans++。
下面给出匈牙利算法的两种实现:
/*DFS实现二分图的最大匹配*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define MAXN 1010
int Nx , Ny;/*Nx Ny分别表示的是左右两边的最大的集合的个数*/
int G[MAXN][MAXN];
int Mx[MAXN] , My[MAXN];/*Mx , My分别表示的是左右两边是否和另一边相连*/
bool mark[MAXN];/*标记右边的点是否被匹配过*/
/*查找增广路*/
bool FindPath(int u){
/*枚举所有的右边集合的点*/
for(int i = 1 ; i <= Ny ; i++){/*注意这个地方下标是从0开始还是1*/
if(G[u][i] && !mark[i]){
mark[i] = true;
if(My[i] == -1 || FindPath(My[i])){
/*互换*/
My[i] = u;
Mx[u] = i;
return true;
}
}
}
return false;
}
/*求最大的匹配*/
int MaxMatch(){
int cnt = 0;
memset(Mx , -1 , sizeof(Mx));/*左边集合初始话为空*/
memset(My , -1 , sizeof(My));/*右边集合初始化为空*/
/*每一次都找左边一个未匹配的点进行找增广路*/
for(int i = 1 ; i <= Nx ; i++){/*注意这个地方下标是从0开始还是1*/
if(Mx[i] == -1){
memset(mark , 0 , sizeof(mark));
if(FindPath(i))
cnt++;
}
}
return cnt;
}
int main(){
/*建模*/
printf("%d\n" , MaxMatch());
return 0;
}
2 BFS实现二分图的最大匹配
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define MAXN 1010
int Nx , Ny;/*左边集合和右边集合*/
int G[MAXN][MAXN];/*存储关系的矩阵*/
int Mx[MAXN] , My[MAXN];/*左边和右边点和另外边相连的编号*/
int pre[MAXN] , Q[MAXN];
int mark[MAXN];
int MaxMatch(){
int ans = 0;
int front , rear;
/*把左边和右边集合置为空*/
memset(Mx , -1 , sizeof(Mx));
memset(My , -1 , sizeof(My));
memset(mark , -1 , sizeof(mark));
for(int i = 1 ; i <= Nx ; i++){/*注意下标是从1开始还是0开始*/
if(Mx[i] == -1){
front = rear = 0;
Q[rear++] = i;
pre[i] = -1;
bool flag = 0;
while(front < rear && !flag){
int u = Q[front];
for(int v = 1 ; v <= Ny && !flag ; v++){/*注意下标是从1开始还是0开始*/
if(G[u][v] && mark[v] != i){
mark[v] = i;
Q[rear++] = My[v];
if(My[v] >= 0)
pre[My[v]] = u;
else{
flag = 1;
int d = u , e = v;
while(d != -1){
int t = Mx[d];
Mx[d] = e;
My[e] = d;
d = pre[d];
e = t;
}
}
}
}
front++;
}
if(Mx[i] != -1)
ans++;
}
}
return ans;
}
int main(){
/*建模*/
printf("%d\n" , MaxMatch());
return 0;
}