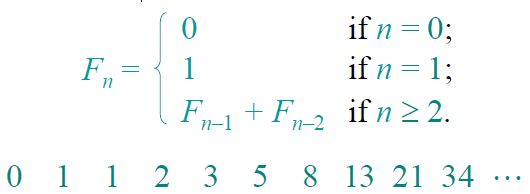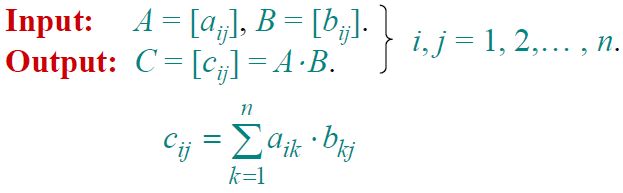MIT算法导论——第三讲.The Divide-and-Conquer
本栏目(Algorithms)下MIT算法导论专题是个人对网易公开课MIT算法导论的学习心得与笔记。所有内容均来自MIT公开课Introduction to Algorithms中Charles E. Leiserson和Erik Demaine老师的讲解。(http://v.163.com/special/opencourse/algorithms.html)
第三节-------分治法 The Divide-and-Conquer
这节课的主要内容是介绍分治法的思想,以及一些应用分治法思想的算法示例,并结合上节课的主定理方法分析算法的性能。
所谓分治法,即分而治之,各个击破。其一般的算法设计步骤是:
1、Divide。即分,将问题拆分成几个子问题;
2、Conquer。即治,通过递归的方法分别解决第一步中子问题;
3、Combine。即合,将各个子问题的结果合并起来便得到整个问题的解决方案。
一、归并排序
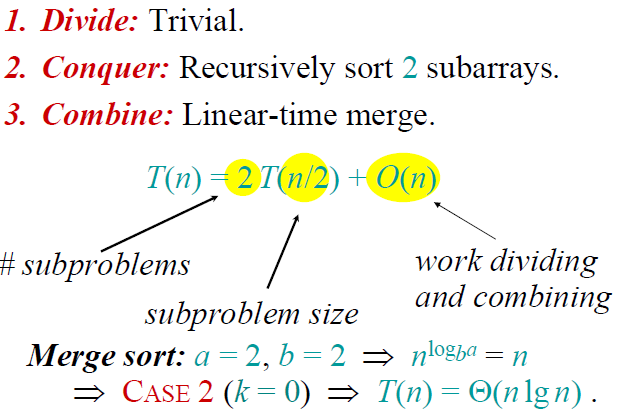
如下图所示是归并排序中的分治法思想,根据设计思想便很容易得到归并排序的效率递归式。得到递归式后,便容易发现其满足主定理方法的Case 2,因此得到归并排序的复杂度为Θ(nlgn)。
二、二分查找
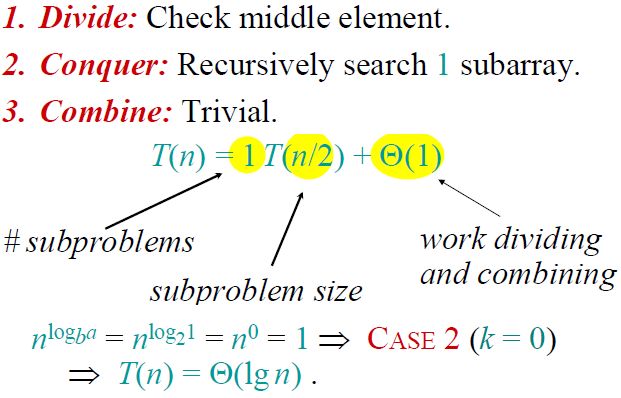
如下图所示是二分查找中的分治法思想,同理得到递归式后,便容易发现其满足主定理方法的Case 2,因此得到归并排序的复杂度为Θ(lgn)。
三、乘方a^n
四、计算斐波那契数列
Fibonacci数列应该也算是耳熟能详,它的递归定义如上图所示。求解斐波那契数列的方法也较多,主要有如下几种。
1. 朴素递归算法(Naive recursive algorithm)
这时的算法效率为Ω(φ^n),指数级别的。其中φ = (1 + 5^½) / 2,即黄金分割比率。
2. 朴素递归平方算法(Naive recursive squaring)
这个算法主要根据斐波那契数列的一条数学性质而来。该性质表明,斐波那契数列F(n)即为φ^n / 5^½向下取整。这样,问题的求解于是变成了一个求乘方的问题,所以算法的效率为Θ(lgn)。
但是这个方法是不太靠谱的,主要是当n比较大时,由于硬件的限制计算机中的浮点运算得到的结果与真实值就产生误差了。
3. 自底向上算法(Bottom-up)
考虑到1中的简单递归算法,为了求解F(n),需要同时递归求解F(n - 1)和F(n - 2),显然这样就做了大量的重复工作。采用自底向上的算法即可避免这样的冗余。要计算F(n),则依次计算F0,F1,F2。。。Fn,这时计算Fn只需要利用前两个结果即可,这样算法效率提高到了Θ(n)。
4. 递归平方算法(Recursive squaring)
该算法也是基于一个定理,定理以及证明过程如下图所示。这样,问题的求解即成为了矩阵的乘方问题,算法效率于是提高到了Θ(lgn)。
五、矩阵乘法
如上图所示即为矩阵乘法问题的描述,关于矩阵的乘法目前的主要方法有如下几种。
1. 常规算法(Standard algorithm)
矩阵的乘法,首先想到的当然就是如下的算法,不难看出该算法的效率为Θ(n^3)。
for i ← 1 to n
do for j ← 1 to n
do c[i][j] ← 0
for k ← 1 to n
do c[i][j] ← c[i][j] + a[i][k]⋅ b[k][j]
2. 分治法算法(Divide-and-conquer algorithm)
矩阵乘法中采用分治法,第一感觉上应该能够有效的提高算法的效率。如下图所示分治法方案,以及对该算法的效率分析。有图可知,算法效率是Θ(n^3)。算法效率并没有提高。

3. Strassen算法(Strassen's algorithm)
鉴于2中的分治法方案无法有效提高算法的效率,要想提高算法效率,由主定理方法可知必须想办法将2中递归式中的系数8减少。Strassen提出了一种将系数减少到7的分治法方案,如下图所示。
很难想象Strassen是如何想出这个方案的,不过它确实将原来递归式中系数由8减小到了7。如下图所示是该算法的算法效率分析:
这样,Strassen算法将矩阵的乘法效率提高到了Θ(n^2.81)。尽管这个2.81在数字上看起来并没有提高多少,但是由于算法效率本身就是指数级的,所以当n比较大时(n ≥ 30在现代的机器上),Strassen算法的优势便已经很明显了。
当然,还有很多关于矩阵运算的优化算法。现在理论上矩阵乘法的效率最好的是:Θ(n^2.376…)。但是在这众多的优化算法中,Strassen算法却是最简单的。
关于Introduction to Algorithms更多的学习资料将继续更新,敬请关注本博客和新浪微博Sheridan。