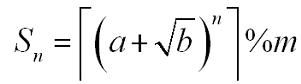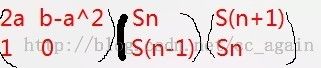数学公式+矩阵快速幂 hdu-4565 So Easy!

题目链接：

http://acm.hdu.edu.cn/showproblem.php?pid=4565

题目大意：

求的值。

解题思路：

因为(a-1)^2<b<a^2,所以a-1<sqrt(b)<a  所以 0<（a-sqrt(b))^n <1  而p=（a+sqrt(b))^n+(a-sqrt(b))^n为整数，所以Sn=p;

再构造递推关系，Sn*（a+sqrt(b)+a-sqrt(b))=S(n+1)+(a^2-b)*S(n-1)

所以S(n+1)=2a*Sn+(b-a^2)*S(n-1).

构造矩阵得   

直接用快速幂相乘即可。

代码：

#include<iostream>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<algorithm>
#include<vector>
#include<map>
#include<set>
#include<stack>
#include<list>
#include<queue>
#define eps 1e-6
#define INF 0x1f1f1f1f
#define PI acos(-1.0)
#define ll __int64
#define lson l,m,(rt<<1)
#define rson m+1,r,(rt<<1)|1
//#pragma comment(linker, "/STACK:1024000000,1024000000")
using namespace std;

/*
freopen("data.in","r",stdin);
freopen("data.out","w",stdout);
*/
#define Maxn 3
ll a,b,n,m;


struct Mar
{
   int r,c;
   ll sa[Maxn][Maxn];
   void init(int a,int b)
   {
      r=a,c=b;
      memset(sa,0,sizeof(sa));
   }
};

Mar mar[35];
Mar operator * (const Mar & a,const Mar &b)
{
   Mar c;
   c.init(a.r,b.c);
   for(int k=1;k<=a.c;k++)
   {
      for(int i=1;i<=c.r;i++)
      {
         if(a.sa[i][k]==0)
            continue;
         for(int j=1;j<=c.c;j++)
         {
            if(b.sa[k][j]==0)
               continue;
            c.sa[i][j]=(c.sa[i][j]+a.sa[i][k]*b.sa[k][j])%m;
         }
      }
   }
   return c;
}
void pre()
{
   mar[0].init(2,2); //预处理 矩阵的偶次方
   mar[0].sa[1][1]=(2*a)%m,mar[0].sa[1][2]=((b-a*a)%m+m)%m;
   mar[0].sa[2][1]=1%m,mar[0].sa[2][2]=0;

   for(int i=1;i<31;i++)
      mar[i]=mar[i-1]*mar[i-1];
   return ;
}


int main()
{
   while(scanf("%I64d%I64d%I64d%I64d",&a,&b,&n,&m)!=EOF)
   {
      pre();
      Mar ans;
      ans.init(2,1);
      ans.sa[1][1]=(2*a)%m,ans.sa[2][1]=(2)%m;
      n--;
      for(int i=0;i<31&&n;i++) //最多只有31位，所以只需预处理到60次方
      {
         if(n&1)
            ans=mar[i]*ans;
         n>>=1;
      }
      printf("%I64d\n",ans.sa[1][1]);
   }
   return 0;
}