AffineTransform（仿射变换）

 

一个任意的仿射变换都能表示为 乘以一个矩阵 (线性变换) 接着再 加上一个向量 (平移)。 我们能够用仿射变换来表示:

• 旋转 (线性变换)
• 平移 (向量加)
• 缩放操作 (线性变换)

我们通常使用 2 x 3 矩阵来表示仿射变换(以下需要一些线性代数的知识)。

A=[abcd]2×2,B=[txty]2×1M=[AB]=[abcdtxty]2×3A=[acbd]2×2,B=[txty]2×1M=[AB]=[actxbdty]2×3

 

用矩阵A和B对二维向量X做变换，那上式也可表示为

T=A⋅[xy]+B或T=M⋅[xy1]TT=[ax+cy+txbx+dy+ty]T=A⋅[xy]+B或T=M⋅[xy1]TT=[ax+cy+txbx+dy+ty]

 

单位矩阵，主对角线为1，其他都为0的矩阵

⎡⎣⎢⎢⎢⎢10⋮001⋯⋯⋱⋯0⋮⋮1⎤⎦⎥⎥⎥⎥[10⋯001⋮⋮⋱⋮0⋯⋯1]

 

CGAffineTransform官方定义

struct CGAffineTransform { CGFloat a, b, c, d; CGFloat tx, ty; }; 

虽然结构体中只有a,b,c,d,tx,ty 6个参数，但其实还有3个固定的参数[0,0,1]来组成3x3的矩阵。

PS:anchorPoint定义了应用变换的坐标系的原点。

仿射变换表示为一个3x3的矩阵如下:

⎡⎣⎢⎢⎢actxbdty001⎤⎦⎥⎥⎥[ab0cd0txty1]

 

对于一个CGPoint(x, y), 经过以上仿射变换后为（x’, y’）,可表示为

[x′y′1]=[xy1]×⎡⎣⎢⎢⎢actxbdty001⎤⎦⎥⎥⎥[x′y′1]=[xy1]×[ab0cd0txty1]

 

即公式(1):

x′=ax+cy+txy′=bx+dy+tyx′=ax+cy+txy′=bx+dy+ty

 

identity矩阵

/* The identity transform: [ 1 0 0 1 0 0 ]. */ CG_EXTERN const CGAffineTransform CGAffineTransformIdentity CG_AVAILABLE_STARTING(__MAC_10_0, __IPHONE_2_0); 

identity矩阵可以表示为

⎡⎣⎢⎢100010001⎤⎦⎥⎥[100010001]

代入公式（1），的得到

x′=1x+0y+0y′=0x+1y+0x′=1x+0y+0y′=0x+1y+0

整理后得到

x′=xy′=yx′=xy′=y

 

identity仿射矩阵计算后的坐标也就是坐标自己本身。

CGAffineTransformMakeTranslation方法

/* Return a transform which translates by `(tx, ty)':  t' = [ 1 0 0 1 tx ty ] */ CG_EXTERN CGAffineTransform CGAffineTransformMakeTranslation(CGFloat tx, CGFloat ty) CG_AVAILABLE_STARTING(__MAC_10_0, __IPHONE_2_0); 

CGAffineTransformMakeTranslation是一个进行平移的方法，根据注释得到的矩阵为

⎡⎣⎢⎢⎢10tx01ty001⎤⎦⎥⎥⎥[100010txty1]

代入公式（1），的得到

x′=1x+0y+txy′=0x+1y+tyx′=1x+0y+txy′=0x+1y+ty

整理后得到

x′=x+txy′=y+tyx′=x+txy′=y+ty

 

CGAffineTransformMakeTranslation也就是所对原来坐标进行一个平移的操作，在x轴方向上移动tx，在y轴方向上移动ty。

CGAffineTransformMakeScale方法

/* Return a transform which scales by `(sx, sy)':  t' = [ sx 0 0 sy 0 0 ] */ CG_EXTERN CGAffineTransform CGAffineTransformMakeScale(CGFloat sx, CGFloat sy) CG_AVAILABLE_STARTING(__MAC_10_0, __IPHONE_2_0); 

CGAffineTransformMakeScale是一个进行缩放的方法，根据注释得到的矩阵为

⎡⎣⎢⎢⎢sx000sy0001⎤⎦⎥⎥⎥[sx000sy0001]

代入公式（1），的得到

x′=sxx+0y+0y′=0x+sxy+0x′=sxx+0y+0y′=0x+sxy+0

整理后得到

x′=sxxy′=syyx′=sxxy′=syy

 

CGAffineTransformMakeScale方法在x轴上缩放sx，在y轴上缩放sx

CGAffineTransformMakeRotation方法

/* Return a transform which rotates by `angle' radians:  t' = [ cos(angle) sin(angle) -sin(angle) cos(angle) 0 0 ] */ CG_EXTERN CGAffineTransform CGAffineTransformMakeRotation(CGFloat angle) CG_AVAILABLE_STARTING(__MAC_10_0, __IPHONE_2_0); 

CGAffineTransformMakeRotation是一个进行旋转的方法，根据注释得到的矩阵为

⎡⎣⎢⎢cosα−sinα0sinαcosα0001⎤⎦⎥⎥[cos⁡αsin⁡α0−sin⁡αcos⁡α0001]

 

1、证明x'和y'构成圆方程

代入公式（1），的得到

x′=cosαx−sinαy+0y′=sinαx+cosαy+0x′=cos⁡αx−sin⁡αy+0y′=sin⁡αx+cos⁡αy+0

整理后得到

x′=cosαx−sinαyy′=sinαx+cosαyx′=cos⁡αx−sin⁡αyy′=sin⁡αx+cos⁡αy

两边都平方，得到

(x′)2=cos2αx2−2sincosα+sin2αy2(y′)2=sin2αx2+2sincosα+cos2αy2(x′)2=cos2⁡αx2−2sin⁡cos⁡α+sin2⁡αy2(y′)2=sin2⁡αx2+2sin⁡cos⁡α+cos2⁡αy2

两式左右都相加得到

(x′)2+(y′)2=(cos2α+sin2α)x2+(2sincosα−2sincosα)+(sin2α+cos2α)y2(x′)2+(y′)2=(cos2⁡α+sin2⁡α)x2+(2sin⁡cos⁡α−2sin⁡cos⁡α)+(sin2⁡α+cos2⁡α)y2

 

化简后得到

(x′)2+(y′)2=x2+y2=r2(x′)2+(y′)2=x2+y2=r2

 

直接就是圆的方程，这只是证明x’ 与 y’在变换后任然在与x 和 y 在以(0,0)为圆心的圆上。

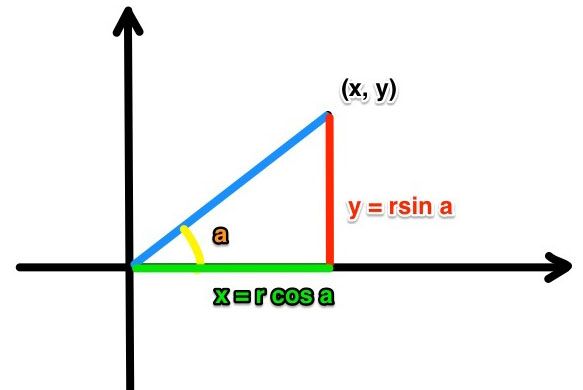
2、真正的推导过程

根据上图用三角函数表示公式(1)

xyx′y′=rcosθ=rsinθ逆时针旋转α后=rcos(θ+α)=rcosθcosα−rsinθsinα将(2)式代入=cosαx−sinαy=rsin(θ+α)=rsinθcosα+rcosθsinα将(2)式代入=sinαx+cosαyx=rcos⁡θy=rsin⁡θ逆时针旋转α后x′=rcos⁡(θ+α)=rcos⁡θcos⁡α−rsin⁡θsin⁡α将(2)式代入=cos⁡αx−sin⁡αyy′=rsin⁡(θ+α)=rsin⁡θcos⁡α+rcos⁡θsin⁡α将(2)式代入=sin⁡αx+cos⁡αy

 

CGAffineTransformMakeRotation方法用来计算出原来点(x,y)旋转α°之后的(x',y')，即将原来的旋转α°。也就是将view或者layer以anchorPoint为中心点旋转α°