高斯滤波与SIFT特征检测

SIFT是半年前看的起一个纯外文文献，现在做一个总结归纳。

1.滤波：

信号在传输过程中会有噪声，于是通过一定的方法滤波去噪。

二维图像上的边缘，角点，纹理对于图像特征抽取，三维重建，物体定位有比较重要的作用，但是噪声对于这些有比较大的影响，产生虚假特征点等。

于是我们要对图像做一个类似预处理的滤波。

2.高斯滤波：

比如一副图像，有许多噪声点，我们可以通过每个像素周围8个像素的平均作为这个像素的实际值，也就是做一个平滑处理。而高斯滤波则采用一定的加权方式来经行这样的处理，这个方式就是正态分布加权。

下图是二维高斯函数（正太分布函数）的三维图：

我们把它离散化，去Z值作为相应（x,y）的权值，对中心像素一定范围的像素加权平均，作为中心像素的像素值。

比如我们去3*3的一个像素采样区间，根据高斯函数，可以得到每个采样点的高斯权值为一下矩阵：

然后用对原始图像做加权滤波处理，即可得到我们要的平滑结果。

高斯滤波是一种线性平滑滤波，适用于消除高斯噪声，广泛应用于图像处理的减噪过程。

通俗的讲，高斯滤波就是对整幅图像进行加权平均的过程，每一个像素点的值，都由其本身和邻域内的其他像素值经过加权平均后得到。高斯滤波的具体操作是：用一个模板（或称卷积、掩模）扫描图像中的每一个像素，用模板确定的邻域内像素的加权平均灰度值去替代模板中心像素点的值。

3.为什么用高斯滤波。

A.单值函数。

B.旋转不变性。

C.证明能有效去除服从正太分布的噪声。

4.高斯差分函数：

上面说的是高斯滤波函数，目的只是引出下面的高斯差分函数：

高斯差分函数也就是不同参数值得高斯滤波后的图像的差。

 A = Process(Im, 0.3, 0.4, x);
 B = Process(Im, 0.6, 0.7, x);

C=A-B，即为其高斯差分。

5.高斯差分的作用：

通过高斯差分后得到的三维极值特征点作，具有很好的稳定性和抗干扰性，对基于图像平移、旋转、缩放，光照，仿射、3D投射以及光照等条件的变化不敏感。有利于后期的图像配准。

6.利用高斯差分，提取sift特征。

上述那么多都是为下面特区sift特征做准备，sift特征点具有尺度不变，旋转不变，光照不变的特性，是比较好的局部特征提取算子。

1）。首先简单介绍一个一个名词：octave，八度，scale，尺度。如下如：

上图有两个octave，每个octave五个scale。

每个octave中，左边每一副是原图像卷积不同的参数的高斯函数所得，如下：

由图片size决定建几个塔，每塔几层图像(S一般为3-5层)。0塔的第0层是原始图像(或你double后的图像)，往上每一层是对其下一层进行Laplacian变换（高斯卷积，其中σ值渐大，例如可以是σ, k*σ, k*k*σ…），直观上看来越往上图片越模糊。塔间的图片是降采样关系，例如1塔的第0层可以由0塔的第3层down sample得到，然后进行与0塔类似的高斯卷积操作。

右边的图像时通过左边的高斯卷积做的差，即高斯差分。

2）。尺度空间极值点检测

如上图，一个中心像素的相邻26个点中，如果这个点领域类最大或最小，则作为关键点。

上述过程我们通过好几个尺度的高斯差分来检测关键点，实现了尺度不变性。

3）。取主方向

我们通过中心像素的领域信息，为每个特征点定一个主方向，每次匹配的时候，对其主方向后再匹配，就能够实现旋转不变的特性。

我们对所有像素做如下处理，得到每个像素的领域信息：

每个像素都计算得到这两个值，一个是领域值，一个是领域方向，其中L为其所在的尺度。

接着我们用这些信息为特征点顶一个主方向。

引入一个名词：统计直方图。就是统计每个统计区间所具有的个数。

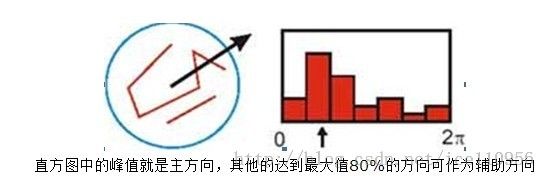
我们以特征点为中心的一个领域取样，计算上面两个值，然后做统计直方图。如下如：

上图中我们选取16个取样点进行取样，得到16个像素的长度和方向。然后做直方图统计，最多的那个方向作为特征点的主方向。

如上图，我们通过一个圆形的领域得到许多领域方向，绘制成左边的统计直方图，选取其峰值，即第二个值，作为特征点的主方向。

经过这一步，我们确定了特征点的主方向。也就是实现了旋转不变性。

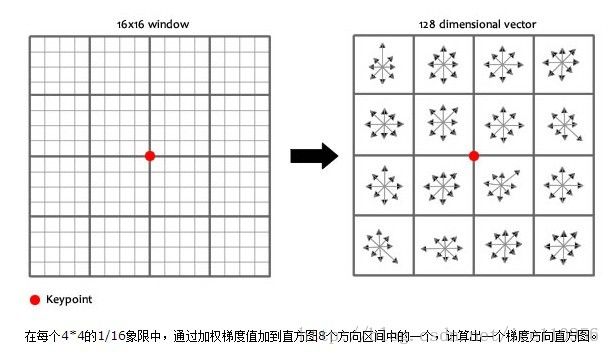
4）。生成特征描述算子

如上图，选取16*16的领域，加权平均得到右边的8个方向，16副算子，也就是8*16=128维的算子。我们再对这个算子做归一化处理，就可以实现光照不变的特性。

需要注意的是，不管是取主方向，还是计算128维的算子，都可使用高斯下降函数降低远离中心的权重。

依照上面三个步骤，我们得到了特征点，主方向，128维算子，其中用高斯差分空间极值点得到的特征点是尺度无关的，取领域像素得到的主方向是旋转不变的，128维算子归一化后，是光照不变的。

5）。匹配：

A,B 两幅图，分别作了上述的计算处理，得到许多关键点和关键点的主方向，128维算子。匹配的时候，我们两个关键点匹配之前，先校准其主方向，然后用欧式距离计算。

文章参考如下几篇文章：

http://blog.csdn.net/likezhaobin/article/details/6835049

http://lixiangtao2002.blog.163.com/blog/static/1819294772012439227366/

http://blog.csdn.net/abcjennifer/article/details/7639488