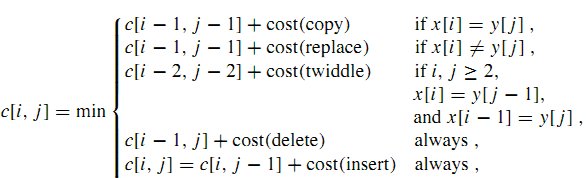编辑距离

问题定义：

    给出源文本串X[l..m]和目标文本串y[1..n] 和 一些操作及代价，求X到Y的编辑距离：将串X转化为串Y的最"便宜"的转换序列的代价

六种变换操作：

       1、删除(delete)操作：源串中的单个字符可被删除

       2、替换(replace)操作：源串中的单个字符可被替换为任意字符

       3、复制(copy)操作：源串中的单个字符被复制到目标串中

       4、插入(insert)操作：源串中的单个字符字符可被插入到目标串的任意位置

       5、交换(twiddle)操作：源串中的两个相邻字符可进行交换并复制到目标串中去

       6、消灭(kill)操作：在完成其它所有操作之后，源串中余下的全部后缀可以全部删除至行末

六种变换操作对应也有相应的代价，如：

    cost(delete)=3;

    cost(replace)=6;

    cost(copy)=5;

    cost(insert)=4;

    cost(twiddle)=4;

    cost(kill)= 被删除的串长 *cost(delete)-1;

举例：

最小代价的转换方式：

代价：copy*3 + replace*2 + delete*1 + insert*3 + twiddle*1 + kill

            = 5*3 + 6*2 + 3*1 + 4*3 + 4*1 + 1*3-1= 48

非最小代价转换方式：

代价：copy*3+replace*1+delete*1+insert*4+twiddle*1+kill

             = 5*3+6*1+3*1+4*4+4*1+2*3-1 = 49

对每一个操作进行分析：

假设，转换后字符可以存在Z中。

复制操作：c[i,j] = c[i - 1,j - 1] + cost(copy)  if x[i] = y[j]

        表示：X的前i-1个字符已经和Y的前j-1个字符匹配，而x[i] = y[j]相等，则只需要将x[i]复制到 z中，就可保证X的前i个字符与Y的前j个字符串是匹配的

替换操作：c[i,j] = c[i - 1,j - 1] + cost(replace)  if x[i]  !=  y[j]

        表示：X的前i-1个字符已经和Y的前j-1个字符匹配，而x[i]  != y[j]相等，则只需要将y[j]替换x[i]而放入z中，就可保证X的前i个字符与Y的前j个字符串是匹配的

交换操作：c[i,j] = c[i - 2,j - 2] + cost(twiddle)  if i,j >= 2 && x[i] = y[j - 1] &&x[i - 1] = y[j]

        表示：X的前i-2个字符已经和Y的前j-2个字符匹配，而x[i] = y[j - 1] && x[i - 1] = y[j]相等，则只需要将x[i] 与x[i - 1]互换复制到z中，就可保证X的前i个字符与Y的前j个字符串是匹配的

删除操作：c[i,j] = c[i - 1,j] + cost(delete)  

        表示：X的前i-1个字符已经和Y的前j个字符匹配，此时X中的第i个字符时多余的，此时我们只需把x[i]删除，就可保证X的前i个字符与Y的前j个字符串是匹配的

插入操作：c[i,j] = c[i,j - 1] + cost(insert)  

        表示：X的前i个字符已经和Y的前j-1个字符匹配，而目标串Y中还有一个字符y[j]在X中不存在，则只需要将y[j]插入z中过来，就可保证X的前i个字符与Y的前j个字符串是匹配的

消灭操作：c[i][n] = MIN(c[m,n], MIN(c[i,n] + cost(kill)))

        表示：X的前i个字符已经和Y串匹配，之后将串X中i + 1到m的字符直接删除，就可保证串X与串Y是匹配的

注意：

1、消灭操作在状态转移方程中用不到，在最后程序的最后在把它用上

2、在不考虑消灭操作时，为了让d[i][j]最小，我们需要枚举以上五个子问题，找最小的转换代价

3、也就是说，五个子问题中，只有一个是我们需要的（它是五者最小值），而为了取最小值，我们需要枚举三个子问题

状态转移方程：

c[i][j]:表示，把源文本串X的前i个字符 转换为 目标串Y的前j个字符串的最小代价

kill操作：c[i][n] = MIN(c[m,n], MIN(c[i,n] + cost(kill)))，其中0<=i<m(从0还是存储)

注意：写状态转移方程时，需要考虑所有能转化为c[i][j]的情况

代码

#include <iostream>
using namespace std;

const int MaxLen = 20; 

char X[] = " algorithm"; //源字符串,第一个为空格
char Y[] = " altruistic";//目标串

int deleteCost = 3; //删除一个字符的代价
int replaceCost = 6;
int copyCost = 5;  
int insertCost = 4;
int twiddleCost = 4;
//cost(kill) = 被删除的串长*cost(delete)-1;

int d[MaxLen][MaxLen] = {{0}};

int Min(int x,int y)
{
	if (x > y)
	{
		return y;
	}
	else
	{
		return x;
	}
}

void PrintD(int lenX,int lenY)
{
	for (int i = 0;i <= lenX;i++)
	{
		for (int j = 0;j <= lenY;j++)
		{
			cout<<d[i][j]<<" ";
		}
		cout<<endl;
	}
}

int EditDistance(int lenX,int lenY)
{
	int del = 0; //删除一个字符的代价
	int replace = 0;
	int copy = 0;  
	int insert = 0;
	int twiddle = 0;

	//初始化边界值
	//原串存在，目标串不存在,把原串中每一个字符都删除
	for (int i = 1;i <= lenX;i++)
	{
		d[i][0] = i * deleteCost;
	}
	//目标串存在，原串不存在,把目标串中每一个字符都插入一遍
	for (int j = 1;j <= lenY;j++)
	{
		d[0][j] = j * insertCost;
	}

	//递推
	for (int i = 1;i <= lenX;i++)
	{
		for (int j = 1;j <= lenY;j++)
		{
			d[i][j] = 100000000;
			if (X[i] == Y[j])
			{
				copy = d[i - 1][j - 1] + copyCost;
				d[i][j] = Min(d[i][j],copy);
				//复制到另一个串中，而不是在源串上直接修改，故需要代价
			}
			else
			{
				replace = d[i - 1][j - 1] + replaceCost;
				d[i][j] = Min(d[i][j],replace);
			}

			del = d[i - 1][j] + deleteCost;
			d[i][j] = Min(d[i][j],del);

			insert = d[i][j - 1] + insertCost;
			d[i][j] = Min(d[i][j],insert);

			if (i >= 2 && j >= 2 && X[i] == Y[j - 1] && X[i - 1] == Y[j])
			{
				twiddle = d[i - 2][j - 2] + twiddleCost;
				d[i][j] = Min(d[i][j],twiddle);
			}
		}
	}
	//处理Kill
	for (int i = 1;i < lenX;i++)
	{
		if (d[lenX][lenY] > d[i][lenY] + deleteCost * (lenX - i) - 1)
		{
			//cost(kill) = 被删除的串长*cost(delete)-1;
			//X的1~i个串 转化成 Y串(1~lenY),X串中剩余的串(i+1~lenX)全部kill掉，
			//删除长度为 lenX - (i + 1)  + 1 = lenX - i
			//注意：for循环中，i不能等于lenX，
			//原因：当i = lenX时，即d[lenX][lenY]时，相当于X串和Y串全部匹配了，不用再Kill了
			
			d[lenX][lenY] = d[i][lenY] + deleteCost * (lenX - i) - 1;
		}
	}
	return d[lenX][lenY];
}

int main()
{
	int lenX = strlen(X) - 1;
	int lenY = strlen(Y) - 1;

	cout<<EditDistance(lenX,lenY)<<endl;

	//PrintD(lenX,lenY);
	system("pause");
	return 0;
}

结果输出：48

编辑距离与LCS的联系：

文本串X要变成文本串Y，要转换的次数：（最少|LenX - LenY|,最多max(LenX,Leny)）

他们两个很相似的原因，在考虑状态转移方程时，需要考虑的地方很相似。我们在状态转移方程的比较可以看出

参考资料

http://blog.csdn.net/mishifangxiangdefeng/article/details/7925025

http://hi.baidu.com/agosits/item/41f42c39e1011c9bc2cf2977